Свойства математического ожидания

Свойство 1.Математическое ожидание постоянной величиныравно самой постоянной:

.

Свойство 2.Постоянный множительможно выносить за знак математического ожидания:

.

Свойство 3.Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

.

Свойство 4.Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:

.

Свойства примем без доказательства.

Как мы отметили выше, математическое ожидание СВ характеризует среднее этой СВ, это центр ее распределения. Вторая отличительная особенность СВ – степень разброса этой величины по отношению к ее центру. Наиболее употребительной оценкой указанного разброса является дисперсия.

На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения СВ и затем найти их средне значение. Однако такой путь ничего не даст, так как среднее значение отклонения, т.е. для любой СВ. Это объясняется тем, что одни возможные отклонения положительны, а другие – отрицательны; в результате их взаимное погашение среднее значение отклонения равно нулю.

Определение 1.7.Дисперсией (рассеянием)дискретной СВ называют математическое ожидание квадрата отклонения СВ от ее математического ожидания:

. (1.3)

Для вычисления дисперсии часто бывает удобно пользоваться следующей теоремой.

Теорема 1.1.Дисперсия равна разности между математическим ожиданием квадрата СВXи квадратом ее математического ожидания:

. (1.4)

Свойства дисперсии

Свойство 1.Дисперсия постоянной величиныравна нулю:

.

Свойство становится ясным, если учесть, что постоянная величина сохраняет одно и то же значение и рассеяние, конечно, не имеет.

Свойство 2.Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

.

Свойство 3.Дисперсия суммы двух независимых СВ равна сумме дисперсий этих величин:

.

Свойство 4.Дисперсия разности двух независимых СВ равна сумме дисперсий этих величин:

.

Свойства примем без доказательства.

Дисперсия как мера рассеивания значений СВ обладает тем недостатком, что ее размерность не совпадает с размерностью СВ (размерность дисперсии – это квадрат размерности СВ).

Поэтому вводится еще одна мера рассеивания с размерностью, совпадающей с размерностью СВ. Это так называемое среднее квадратическое отклонение.

Определение 1.8.Средним квадратическим отклонениемСВXназывают квадратный корень из дисперсии:

. (1.5)

Дадим определение еще одной числовой характеристики, как модаДСВ.

Определение 1.9.Модой M_o ДСВ X называется ее наиболее вероятное значение.

Пример 1.3.СВXзадана законом распределения:

.

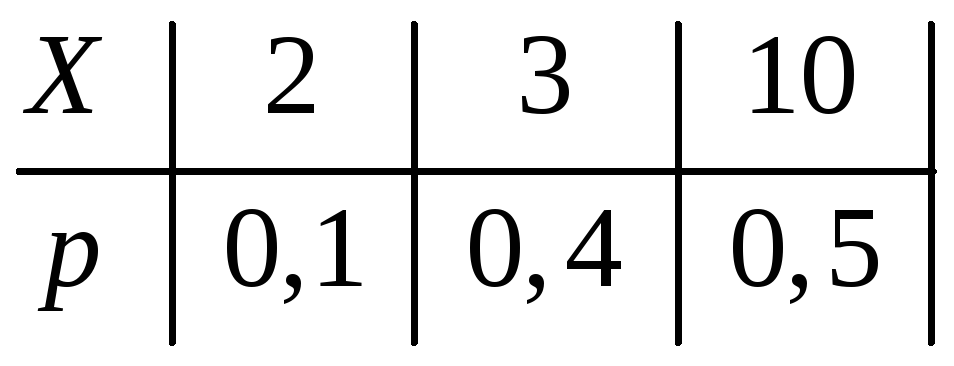Построить функцию распределения и ее график. Найти числовые характеристики заданного закона распределения.

Решение.1) Найдем функцию распределения ДСВX. Значения СВX:разбивают числовую прямую на четыре промежутка.

Если , то.

Если , то.

Если , то.

Если , то.

Таким образом, получаем следующую функцию распределения:

.

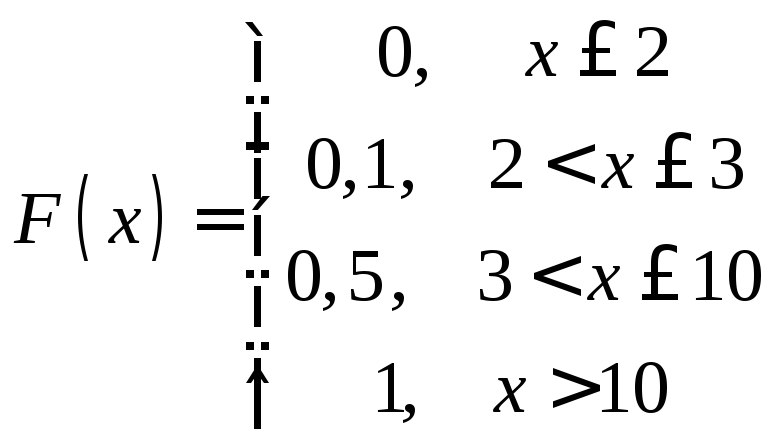График данной функции имеет вид:

2) Найдем числовые характеристики ДСВ X.

Найдем математическое ожидание:

.

Найдем дисперсию:

.

Найдем среднее квадратическое отклонение:

.

Мода соответственно равна M_o=10.



Пример 1.4.Найти закон распределения ДСВ, которая может принимать только два значенияс вероятностьюи(причем), если известны математическое ожиданиеи дисперсия.

Решение.Поскольку, а, то. Тогда имеем следующий закон распределения:

.

По формулам (1.2) и (1.4) получаем:

;

.

Составляем систему уравнений

.

Решив систему уравнений, получаем два решения: ,или,. По условию задачи подходит первое решение.

Итак, ,.