Контрольная работа № 4

По дисциплине «Математика»

Для студентов заочной формы обучения мсф, ртф

Вариант 24

1.Из букв разрезной азбуки составлено слово «геометрия». Карточки с отдельными буквами тщательно перемешивают, затем наугад извлекают и раскладывают их в порядке извлечения. Какова вероятность того, что:

а) получится слово «геометрия»;

б) из трех извлеченных карточек получится слово «тир».

2.Дана электрическая схема, в которой вероятность отказа узловZ_i,, за времяTравнаp₁=0,1;p₂=0,3;p₃=0,2;p₄=0,2;p₅=0,4. Схема выходит из строя, если цепь разомкнута. Какова вероятность того, что цепь не пропустит электрический ток?

3.В трех коробках имеются однотипные конденсаторы. В первой 25 конденсаторов, из них 2 неисправных, во второй – 15, из них 3 неисправных, в третьей – 30, из них 5 неисправных.

а) Найти вероятность того, что наугад взятый конденсатор из случайно выбранной коробки годен к использованию.

б) Наугад взятый конденсатор оказался годным. Из какой коробки он вероятнее всего взят?

4.Записать закон распределения дискретной случайной величиныX. Составить функцию распределенияF(x) и построить ее график. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.

Из 20 книг, стоящих на полке, 8 художественных. Наугад берут 4 книги. СВ X– число художественных книг среди четырех взятых.

5.Дана функция распределенияF(x) СВX. Найти плотность распределенияp(x). Найти математическое ожидание, дисперсию и среднее квадратическое распределение. Найти вероятность попадания СВXна отрезокa;b.

,.

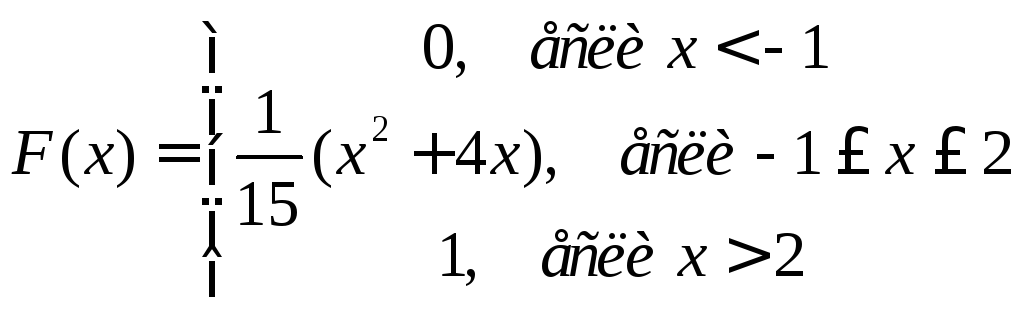6.Длительность времени безотказной работы каждого из пяти модулей технологической системы имеет показательное распределение. Среднее время безотказной работы для каждого модуля равно 700 ч. Технологическая система работает при условии безотказной работы хотя бы четырех модулей. Определить вероятность безотказной работы технологической системы в течение не менее 1000 ч, если время безотказной работы каждого модуля не зависит от времени работы других модулей.

7.Из одной партии диодов были произведены измерения времени восстановления диода (признакX). Результаты измерений (в наносекундах) записаны в виде статистического ряда.

68	73	70	68	61	73	71	72	67	70
65	70	76	68	71	71	68	70	64	64
72	70	70	69	66	70	77	69	71	74
72	72	72	68	70	67	71	67	72	69
66	75	62	69	71	67	70	73	71	74

Произвести статистическую обработку результатов измерений:

1) построить интервальный вариационный ряд;

2) построить гистограмму относительных частот, эмпирическую функцию распределения и ее график (кумулянту);

3) найти выборочные числовые характеристики ;

4) по геометрическим характеристикам и по соотношениям между числовыми характеристиками выдвинуть гипотезу о законе распределения признака X;

5) проверить гипотезу о законе распределения признака Xпо критерию-квадрат при уровне значимости 0,05;

6) найти 95%-ые доверительные интервалы для математического ожидания и среднего квадратического отклонения.

8.Экспериментальная зависимость признакаYот фактораXимеет вид:

Xi	11	13	14	17	19	20	23	25
Yi	118	120	131	137	138	152	160	160

Требуется:

1) найти уравнение линейной регрессии ;

2) найти выборочный коэффициент корреляции ;

3) выяснить значимость уравнения регрессии при ;

4) построить линию регрессии и экспериментальные точки .