
- •Раздел 3
- •1. Основные понятия
- •Генеральная и выборочная совокупность. Вариационный ряд
- •Эмпирическая функция распределения. Полигон. Гистограмма
- •1.3. Статистические оценки параметров распределения
- •Требования, которым должны удовлетворять оцениваемые параметры
- •2. Точечные и интервальные оценки
- •Доверительные интервалы для оценки математического ожидания нормального распределения при известном
- •Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном
- •Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения
- •3. Статистические гипотезы
- •3.1. Основные понятия
- •Критическая область. Область принятия гипотез. Критические точки
- •Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона
- •Правило проверки нулевой гипотезы
- •4. Элементы теории корреляции
- •Свойства коэффициента корреляции
- •5. Элементы дисперсионного анализа
Свойства коэффициента корреляции
Свойство 1.Абсолютная величина выборочного коэффициента корреляции не превосходит единицы.
![]() .
.
В зависимости от того, насколько
![]() приближается к 1, различают слабую,
умеренную и сильную связь, т.е. чем ближе
приближается к 1, различают слабую,
умеренную и сильную связь, т.е. чем ближе
![]() к 1, тем теснее связь.
к 1, тем теснее связь.
Свойство 2.Если выборочный коэффициент корреляции равен нулю и выборочные линии регрессии – прямые, тоXиYне связаны линейной корреляционной зависимостью.
Свойство 3.Если абсолютная величина выборочного коэффициента корреляции равна единице, то наблюдаемые значения признака связаны линейной функциональной зависимостью.
Свойство 4.Если переменныеXиYумножить на одно и то же число, то коэффициент корреляции не изменится.
Из приведенных свойств вытекает смысл
![]() :выборочные коэффициент корреляции
характеризует тесноту линейной связи
между количественными признаками в
выборке: чем ближе
:выборочные коэффициент корреляции
характеризует тесноту линейной связи
между количественными признаками в
выборке: чем ближе
![]() к 1, тем связь сильнее; чем
ближе
к 1, тем связь сильнее; чем
ближе
![]() к 0, тем связь слабее.
к 0, тем связь слабее.
Если выборка имеет достаточно большой объем и хорошо представляет генеральную совокупность (репрезентативна), то заключение о тесноте линейной зависимости между признаками, полученное по данным выборки, в известной степени может быть распределена и на генеральную совокупность.
Если график регрессии
![]() или
или![]() изображается кривой линией, то корреляцию
называюткриволинейной.
изображается кривой линией, то корреляцию
называюткриволинейной.
Например, функции регрессии YнаXмогут иметь вид:
![]() (параболическая корреляция второго
порядка);
(параболическая корреляция второго
порядка);
![]() (параболическая корреляция третьего
порядка);
(параболическая корреляция третьего
порядка);
![]() (гиперболическая корреляция).
(гиперболическая корреляция).
Теория криволинейной корреляции решает те же задачи, что и теория линейной корреляции (установление формы и тесноты корреляционной связи).
Неизвестные параметры уравнения регрессии находят методом наименьших квадратов. Для оценки тесноты криволинейной корреляции служат выборочные корреляционные отношения.
5. Элементы дисперсионного анализа
Дисперсионный анализ был предложен Р. Фишером для решения некоторых задач в области биологических исследований, в частности в сельскохозяйственной статистике. В настоящее время дисперсионный анализопределяется какстатистический метод, предназначенный дляоценки влияния различных факторов на результат эксперимента, в связи с чем область применения этого метода становится значительно шире.
Результатом эксперимента является
некоторая случайная величина
![]() ,
называемая такжерезультативным
признаком. На значения случайной
величины
,
называемая такжерезультативным
признаком. На значения случайной
величины![]() влияет фактор
влияет фактор![]() ,
состоящий из несколькихуровнейилигрупп
,
состоящий из несколькихуровнейилигрупп![]() .
.
Как было отмечено выше, в прикладных
задачах статистического анализа
зависимость между входными переменными
![]() и выходной переменной
и выходной переменной![]() носит стохастический характер. При
изучении стохастических зависимостей
в задачах техники, экономики и т.д. одним
из главных моментов являетсяустановление
вида зависимости
носит стохастический характер. При
изучении стохастических зависимостей
в задачах техники, экономики и т.д. одним
из главных моментов являетсяустановление
вида зависимости ![]() от
от![]() ,
т.е. вида уравнения регрессии – это
задачирегрессионного анализ. Это
связано в первую очередь с необходимостью
прогнозирования исследуемых процессов.
,
т.е. вида уравнения регрессии – это
задачирегрессионного анализ. Это
связано в первую очередь с необходимостью
прогнозирования исследуемых процессов.
В регрессионном анализе изучаются модели вида
![]() ,
(5.1)
,
(5.1)
где
![]() неслучайная
независимая переменная, называемаяфактором;
неслучайная
независимая переменная, называемаяфактором;![]() случайная зависимая
переменная (результативный признак);
случайная зависимая
переменная (результативный признак);![]() случайная переменная,
характеризующая отклонение от линии
регрессии (остаточная переменная).
случайная переменная,
характеризующая отклонение от линии
регрессии (остаточная переменная).
Для того чтобы установить, соответствует ли выбранная регрессионная модель (5.1) экспериментальным данным, используют основное уравнение дисперсионного анализа:
![]() ,
(5.2)
,
(5.2)
где
 общая сумма квадратов отклонений
общая сумма квадратов отклонений![]() от средней, (5.3)
от средней, (5.3)
 сумма квадратов, обусловленная
регрессией, (5.4)
сумма квадратов, обусловленная
регрессией, (5.4)
 остаточная сумма квадратов.
(5.5)
остаточная сумма квадратов.
(5.5)
Для несруппированной выборки формулы (5.3) (5.5) несколько упрощаются:
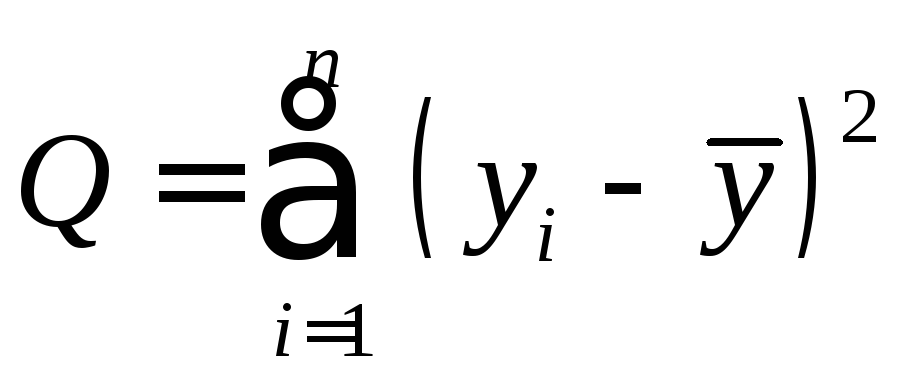 общая сумма квадратов отклонений
общая сумма квадратов отклонений![]() от средней, (5.6)
от средней, (5.6)
 сумма квадратов, обусловленная
регрессией, (5.7)
сумма квадратов, обусловленная
регрессией, (5.7)
 остаточная сумма квадратов.
(5.8)
остаточная сумма квадратов.
(5.8)
Данные в корреляционных таблицах можно
рассматривать как случайные выборки
соответствующих генеральных совокупностей
по некоторым признакам
![]() и
и![]() .
Статистические числовые характеристики
.
Статистические числовые характеристики![]() ,
полученный по данной выборки, являются
оценками для числовых характеристик
,
полученный по данной выборки, являются
оценками для числовых характеристик![]() генеральной совокупности. Выборочный
коэффициент корреляции
генеральной совокупности. Выборочный
коэффициент корреляции![]() и выборочные коэффициенты регрессии
и выборочные коэффициенты регрессии![]() и
и![]() при нормальном распределении случайных
величин
при нормальном распределении случайных
величин![]() и
и![]() также можно рассматривать в качестве
оценок соответствующих коэффициентов
также можно рассматривать в качестве
оценок соответствующих коэффициентов![]() и
и![]() .
.
Так как рассмотренная выборка отобрана
случайна, то еще нельзя заключить, что
коэффициент корреляции генеральной
совокупности
![]() также отличен от нуля.
также отличен от нуля.
При заданном уровне значимости
![]() проверим нулевую гипотезуH0.
проверим нулевую гипотезуH0.
H0: равенство
нулю генерального коэффициента
корреляции, т.е.![]() .
.
Конкурирующая гипотеза H1:![]() .
.
Если нулевая гипотеза будет отвергнута, то это значит, что выборочный коэффициент корреляции значимо отличается от нуля, а X иYкоррелированны, т.е. связаны линейной зависимостью. Если нулевая гипотеза будет принята, то выборочный коэффициент корреляции незначим, аXиYнекоррелированы, т.е. не связаны линейной зависимостью.
Для проверки нулевой гипотезы найдем статистику по следующей формуле:
 ,
,
где
![]() и
и![]() находят по формулам (5.7) и (5.8);n– число наблюдений;l– число групп в корреляционной таблице
или число оцениваемых параметров в
несгруппированной выборке.
находят по формулам (5.7) и (5.8);n– число наблюдений;l– число групп в корреляционной таблице
или число оцениваемых параметров в
несгруппированной выборке.
Для заданного уровня значимости
![]() находят критическое значение распределение
находят критическое значение распределение![]() Фишера при
Фишера при![]() степенях свободы.
степенях свободы.
Если
![]() ,
то уравнение линейной регрессии значимо.
Принимаем конкурирующую гипотезуH1:
,
то уравнение линейной регрессии значимо.
Принимаем конкурирующую гипотезуH1:![]() .
.
Пример 5.1.Экспериментальная зависимость признакаYот фактораXимеет вид:
|
Xi |
2 |
3 |
3,5 |
4 |
5 |
6 |
7 |
8 |
|
Yi |
2 |
1,9 |
2,1 |
2,2 |
2,4 |
2,3 |
2,5 |
2,5 |
Требуется:
1) найти уравнение линейной регрессии
![]() ;
;
2) найти выборочный коэффициент
корреляции
![]() ;
;
3) выяснить значимость уравнения
регрессии при
![]() ;
;
4) построить линию регрессии и
экспериментальные точки
![]() .
.
Решение.
1) Коэффициенты
![]() иbуравнения линейной
регрессии находятся по следующим
формулам:
иbуравнения линейной
регрессии находятся по следующим
формулам:
 ;
;
 ,
,
где
![]() число наблюдений.
В нашем случае
число наблюдений.
В нашем случае![]() .
.
Чтобы определить коэффициенты
![]() иb, а так же коэффициент
корреляции
иb, а так же коэффициент
корреляции
![]() ,составляем расчетную таблицу.
,составляем расчетную таблицу.

Тогда получаем
 ;
;
 .
.
Итак, уравнение линейной регрессии имеет вид:
![]() .
.
2) Выборочный коэффициент корреляции
![]() находится по следующей формуле:
находится по следующей формуле:
 .
.
Тогда получаем
 .
.
3) Выше получили, что коэффициент
корреляции
![]() .
.
Так как рассмотренная выборка отобрана
случайна, то еще нельзя заключить, что
коэффициент корреляции генеральной
совокупности
![]() также отличен от нуля.
также отличен от нуля.
При заданном уровне значимости
![]() проверим нулевую гипотезуH0.
проверим нулевую гипотезуH0.
H0: равенство
нулю генерального коэффициента
корреляции, т.е.![]() .
.
Конкурирующая гипотеза H1:![]() .
.
Если нулевая гипотеза будет отвергнута, то это значит, что выборочный коэффициент корреляции значимо отличается от нуля, а X иYкоррелированны, т.е. связаны линейной зависимостью. Если нулевая гипотеза будет принята, то выборочный коэффициент корреляции незначим, аXиYнекоррелированы, т.е. не связаны линейной зависимостью.
Для проверки нулевой гипотезы найдем статистику по следующей формуле:
 ,
,
где
![]() сумма квадратов,
обусловленная регрессией;
сумма квадратов,
обусловленная регрессией;
![]() остаточная сумма квадратов;
остаточная сумма квадратов;
n– число наблюдений;
l– число групп в корреляционной таблице или число оцениваемых параметров в несгруппированной выборке.
Для определения статистики tсоставляем расчетную таблицу.

Значения
![]() находим из уравнения регрессии, подставляя
соответствующие значения
находим из уравнения регрессии, подставляя
соответствующие значения![]() .
Среднюю выборочную
.
Среднюю выборочную![]() находим следующим образом:
находим следующим образом:
 .
.
Итак, получаем
![]() .
.
В нашем случае число наблюдений
![]() .
Поскольку рассматривается линейная
регрессия, то
.
Поскольку рассматривается линейная
регрессия, то![]() число оцениваемых
параметров.
число оцениваемых
параметров.
При
![]() по таблицам распределения Фишера находим
по таблицам распределения Фишера находим![]() .
.
Вычисляем статистику.
![]() .
.
Так как
![]() ,
то уравнение линейной регрессии значимо.
Принимаем конкурирующую гипотезуH1:
,
то уравнение линейной регрессии значимо.
Принимаем конкурирующую гипотезуH1:![]() .
.
4) Строим линию регрессии и экспериментальные
точки
![]() .
.

