6.5. Определение астрономической единицы (параллакса Солнца)

Если известны радиус Земли R и горизонтальный параллакс Солнца р¤, то по формуле (3.2) легко вычислить среднее расстояние Земли от Солнца, т. е. значение астрономической единицы в километрах. Точность определения астрономической единицы почти целиком зависит от точности горизонтального параллакса Солнца р¤. Однако непосредственное определение горизонтального параллакса Солнца способом, описанным в предыдущем параграфе, дает слишком грубые результаты вследствие удаленности Солнца и больших ошибок наблюдений, возникающих от нагревания инструмента солнечными лучами. Поэтому точное значение горизонтального параллакса Солнца определяется косвенным путем, по измеренному горизонтальному параллаксу планеты, которая подходит к Земле на расстояние меньшее, чем расстояние Земли от Солнца, и наблюдение которой удобно производить.

До XX в. для этой цели использовали наблюдения Марса во время его великих противостояний, когда он находится от Земли на расстоянии около 55 млн. км. (Противостояние планеты называется великим, если она в это время находится вблизи перигелия своей орбиты. Последнее великое противостояние Марса наблюдалось в 1971 г., следующее произойдет в 1988 г.)

Пусть для упрощения задачи в момент великого противостояния Марса (рис. 43) Солнце С, Земля Т и Марс М находятся на одной прямой, причем Земля — на среднем расстоянии а₀= 1 а.е. от Солнца, а Марс — в перигелии, на расстоянии q = a (1 — е), где а — большая полуось и е — эксцентриситет орбиты Марса. Обозначим через р¤ горизонтальный экваториальный параллакс Солнца, через р горизонтальный экваториальный параллакс Марса и через— его геоцентрическое расстояние (т.е. расстояние от Земли), а через R₀— экваториальный радиус Земли. Тогда

R₀ = a₀ sin р¤

и

R₀ = sin p = (q — a₀) sin p = [a(l — е) — a₀]: sin p.

Приравняв правые части и заменив синусы малых углов самими углами, получим

a₀ р¤= [(1 — e) — a₀] × p,

откуда

Отношение вычисляется с большой точностью из теории движения планет по третьему закону Кеплера, а параллакс Марса р и эксцентриситет е его орбиты определяется из наблюдений.

В 1898 г. была открыта малая планета Эрос (или Эрот), которая в моменты своих великих противостояний, повторяющихся через 37 лет, иногда подходит к Земле в 2,5 раза ближе, чем Марс. Первое такое противостояние произошло в феврале 1931 г., когда Эрос приблизился к Земле на расстояние около 0,15 а.е. В это время его параллакс достиг 60". В результате тщательных наблюдений Эроса, произведенных на 24 обсерваториях разных стран по заранее разработанному плану, горизонтальный экваториальный параллакс Солнца получился равным р¤= 8",790 ± 0",001.

Самые точные определения астрономической единицы были произведены в 1961-1963 гг. в СССР и США по радиолокационным наблюдениям Меркурия и Венеры. В результате этих измерений было получено значение а.е., равное 149 598 500 км с ошибкой ±500 км.

р¤ = 8",794 и 1 а.е. = 149,6 × 106 км

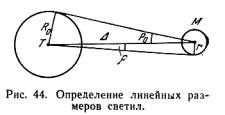
6.6. Определение размеров и формы светил

Угол, под которым с Земли виден диск светила, называется его угловым диаметром. Угловые диаметры некоторых небесных тел (Солнца, Луны, планет) можно определить непосредственно из наблюдений.

Если известен угловой диаметр (или радиус) светила и его расстояние от Земли, то легко вычислить его истинный диаметр (или радиус) в линейных мерах. Действительно, если (рис. 44) r — угловой радиус светила М, — расстояние между центрами светила и Земли, р₀— горизонтальный экваториальный параллакс светила, а R₀и r — линейные радиусы Земли Т и светила М, то r =sin, a R₀=sin p₀, откуда

или, по малости углов и p₀,

Форму небесных тел можно определить, измеряя различные диаметры их дисков. Если тело сплющенное, то один из его диаметров окажется больше, а один — меньше всех других диаметров. Измерения диаметров планет показали, что помимо Земли сплющенную форму имеют Марс, Юпитер, Сатурн, Уран и Нептун.