MATH-krat-teor / Математика-методы решений / Методы решения уравнений, содержащих знак модуль

Методы решения уравнений, содержащих знак модуль.

I) Уравнения вида решаются следующим образом.

Если , то корней нет.

Если , то уравнению соответствует уравнение

Если , то уравнению соответствует равносильная совокупность

II) Уравнения вида решаются следующим образом.

Способ №1

Уравнению соответствует равносильная совокупность систем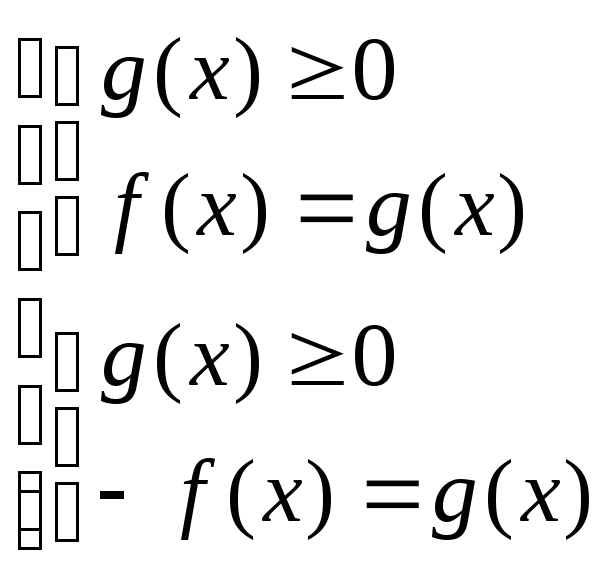

Способ №2

Уравнению соответствует равносильная совокупность систем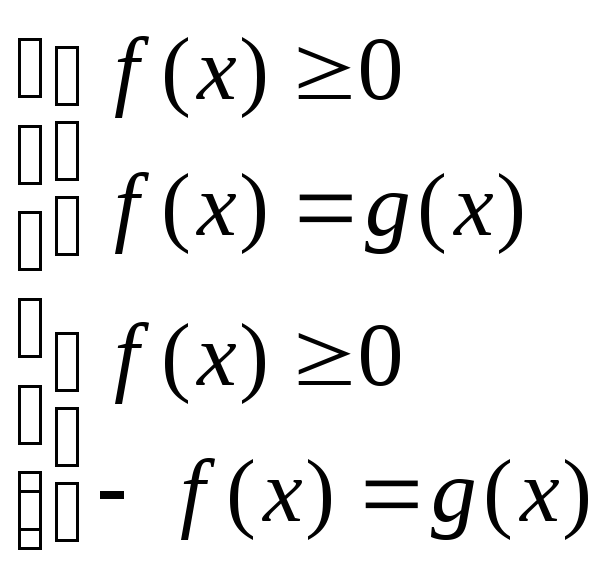

III) Уравнения вида решаются следующим образом.

Способ №1

Уравнению соответствует равносильное уравнение

Способ №2

Уравнению соответствует равносильная совокупность

IV) Уравнения вида и решаются следующим образом.

Уравнению соответствует равносильное неравенство

Уравнению соответствует равносильное неравенство

V) Общая схема решения уравнений содержащих знак модуль.

Например.

Найдем нули выражений, стоящих под знаком модуль.

I) II) III)

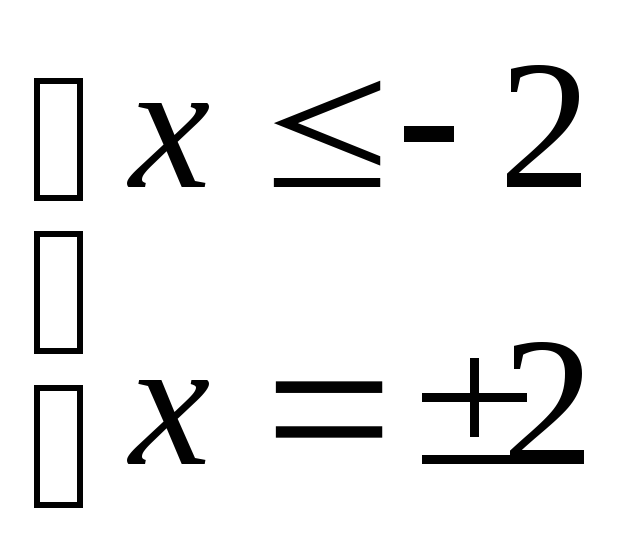
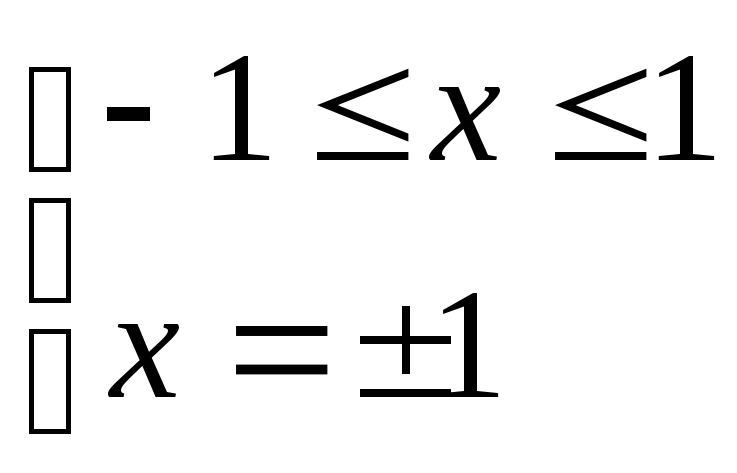
- промежуток

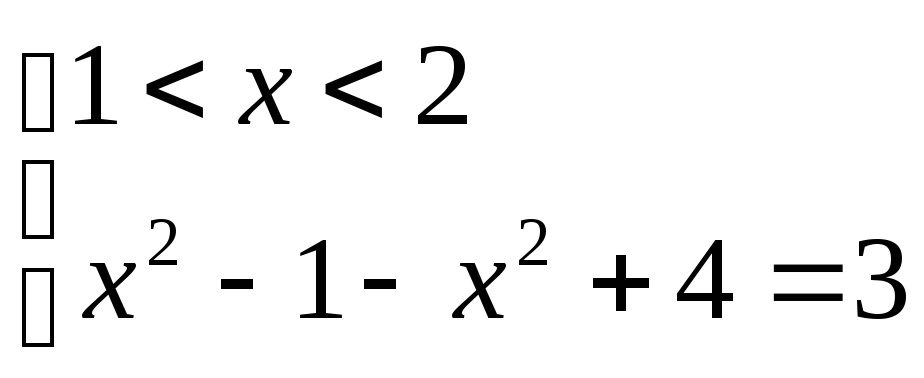IV) V)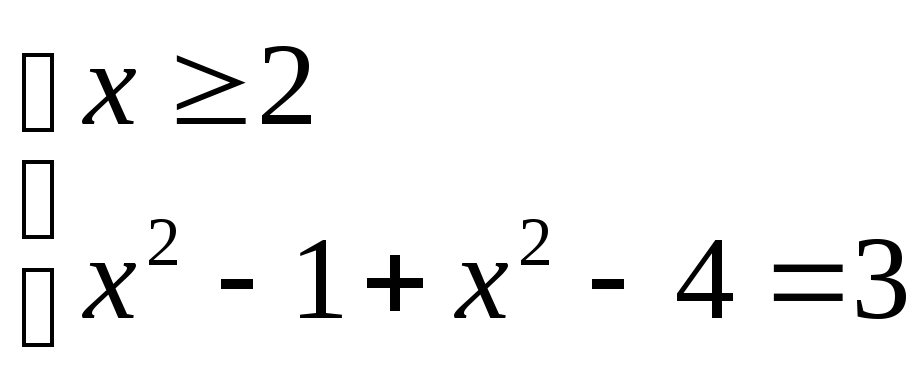

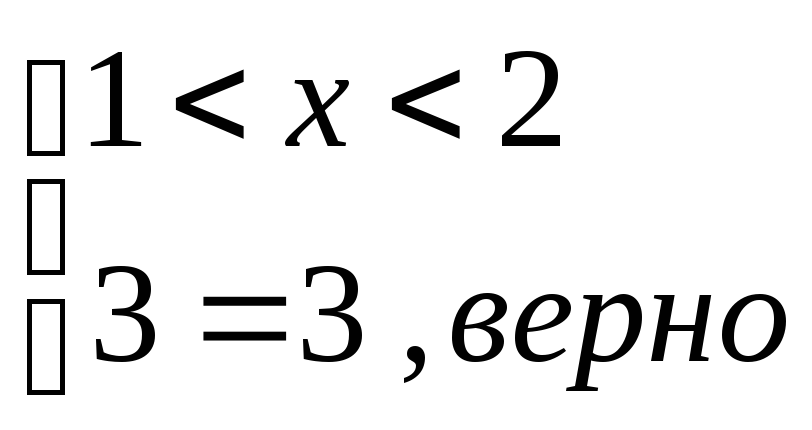
- промежуток

Ответ:

P. S. В уравнениях вида рекомендуется начинать раскрывать с внешнего модуля.