MATH-krat-teor / Математика-методы решений / Методы решения иррациональных уравнений
..doc
Методы решения иррациональных уравнений.
I) Метод возведения в четные степени (неравносильный переход нужна проверка) и нечетные степени (равносильный переход).
II) Уравнения вида
решаются следующим образом.
Уравнению вида
соответствует равносильная система
III) Уравнения вида
решаются следующим образом.
Так как произведение равно нулю тогда и только тогда, когда один из множителей равен нулю, а остальные при этом имеют смысл, то данное уравнение равносильно следующей совокупности.
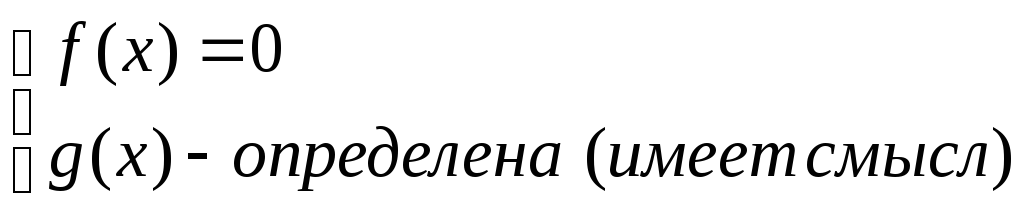или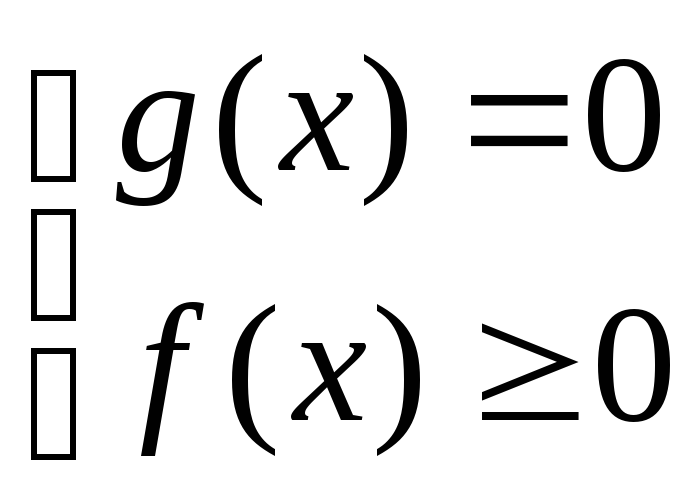 
IV) Уравнения вида
решаются следующим образом.
Уравнению вида
соответствует равносильная система.
Способ №1
Способ
№2
V) Уравнения вида
решаются следующим образом.
Уравнению вида
соответствует равносильная система.
или 
VI) Уравнения вида
решаются следующим образом.
Возведем обе части уравнения в куб.
(1)
(2)
При пепеходе из 1 в 2 происходит не равносильный переход, значит, необходима обязательная проверка.
VII) Уравнения вида
решаются следующим образом.
Уравнению вида
соответствует равносильная совокупность
систем.
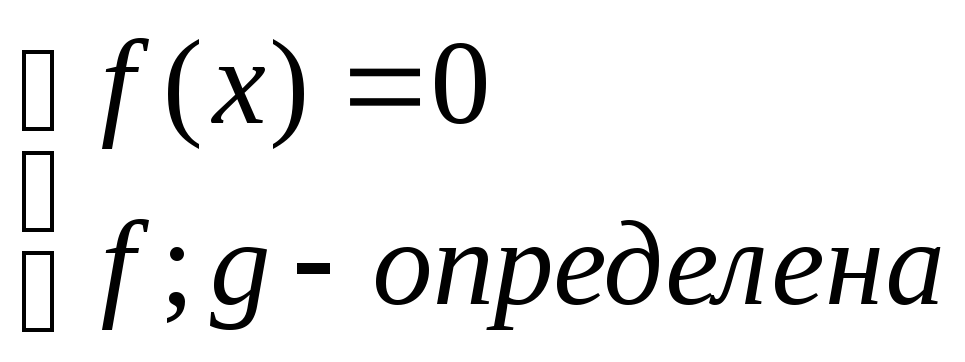
VIII) Уравнения вида
решаются следующим образом.
Уравнению вида
решаются
с помощью введения переменных.
Сводятся к решению системы алгебраических уравнений.
IX) Уравнения вида
решаются следующим образом.
Обе части исходного уравнения умножаются на выражение, сопреженное с сепой частью уравнения и сложением затем исходного и полученного уравнений, что приводит к решениию простейшего иррационального уравнения. (Нужна проверка)
X) Уравнения вида
решаются следующим образом.
Удобно произвести замену.
Исходное уравнение примет вид.
Обычно под знаком одного из радикалов, после такой замены, появляется полный квадрат двух члена.
XI) Уравнения вида
решаются следующим образом.
Теорема. Если
- возростающая функция, то уравнение
и
- равносильны.
Например.
решений
нет
XII) Решение некоторых иррациональных уравнений можно свести к однородным уравнениям.
Например.
Пусть
,
,
тогда
