MATH-krat-teor / Математика-методы решений / Методы решения неравенств, содержащих знак модуль

Методы решения неравенств, содержащих знак модуль.

I) Неравенства вида решаются следующим образом.

Если , то решений нет

Если , то

Если , то неравенству равносильна система

II) Неравенства вида решаются следующим образом.

Если , то решений нет

Если , то решений нет

Если , то неравенству равносильна система

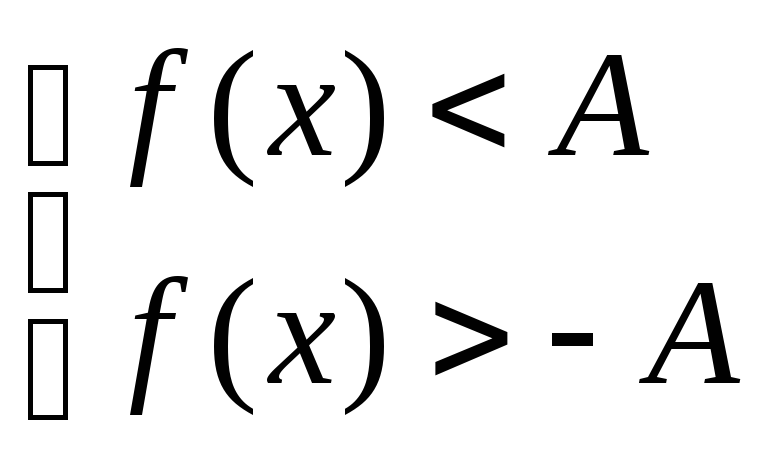
III) Неравенства вида решаются следующим образом.

Если , то неравенство верно для любых х из области определения

Если , то неравенство верно для любых х из области определения

Если , то неравенству равносильна совокупность

IV) Неравенства вида решаются следующим образом.

Если , то неравенство верно для любых х из области определения

Если , то неравенству равносильна система

Если , то неравенству равносильна система

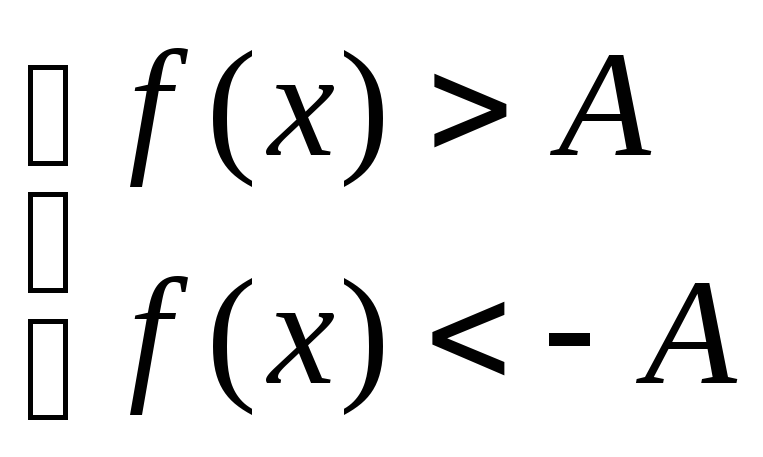
V) Неравенства вида решаются следующим образом.

Если , то решений нет.

Если , то решений нет.

Если , то неравенству равносильна система

VI) Неравенства вида решаются следующим образом.

Если , то решений нет.

Если , то неравенству соответствует уравнение

Если , то неравенству равносильна система

VII) Неравенства вида решаются следующим образом.

Если , то неравенство верно для любых значений x из области определения неравенства

Если , то неравенству равносильна система

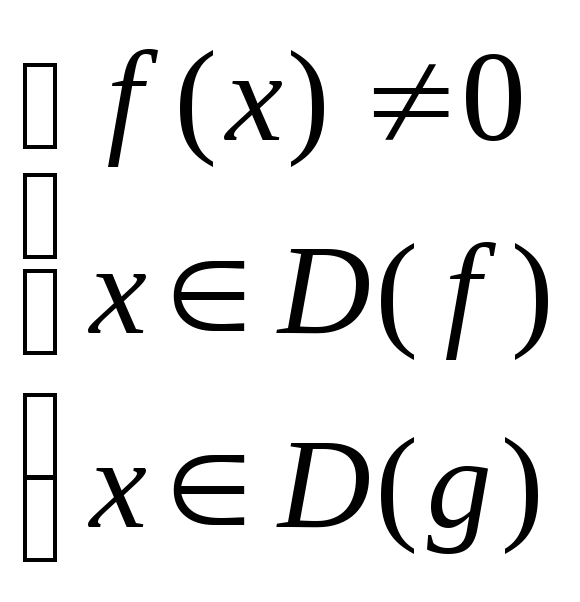
Если , то неравенству равносильна совокупность

VIII) Неравенства вида решаются следующим образом.

Если , то неравенство верно для любых значений x из области определения неравенства

Если , то неравенство верно для любых значений x из области определения неравенства

Если , то неравенству равносильна совокупность

IX) Неравенства вида и решаются следующим образом.

Неравенству соответствует неравенство (либо общий способ)

Неравенству соответствует неравенство (либо общий способ)

X) Решение неравенств используя определение модуля (общий способ).

P.S

Любое неравенство можно решит общим способом.