MATH-krat-teor / Математика-методы решений / Методы решения уравнений высших степеней

Методы решения уравнений высших степеней.

I) Решение уравнений с помощью деления в столбик.

Очевидно - корень уравнения

Очевидно - корень уравнения

Ответ: -5;2;3;4

II) Возвратные уравнения и к ним сводящиеся.

Уравнение называется возвратным, если в нем коэффициенты равноудаленные от концов совпадают, т.е. , ,

1) Возвратные уравнения четной степени.

т.к. - не является корнем уравнения, то разделим обе части уравнения на .

Введем замену.

Пусть , , получим

;

Вернемся к замене.

или

корней нет

Ответ:

2) Возвратные уравнения нечетной степени.

Любое возвратное уравнение нечетной степени сводится к квадратному уравнению четной степени, т.к у любого возвратного ур–ия нечетной степени один из корней всегда равен –1

Очевидно - корень уравнения.

или

т.к - не является корнем уравнения, то разделим обе части

уравнения на

Введем замену.

Пусть , , , получим

или или

корней нет

Ответ: , ,

III) Уравнения вида, где решаются как возвратные.

IV) Замена переменных по явным признакам.

V) В следующих уравнениях используется “идея однородности”.

Пример №1

Введем замену.

Пусть , , тогда

1) если , тогда , тогда

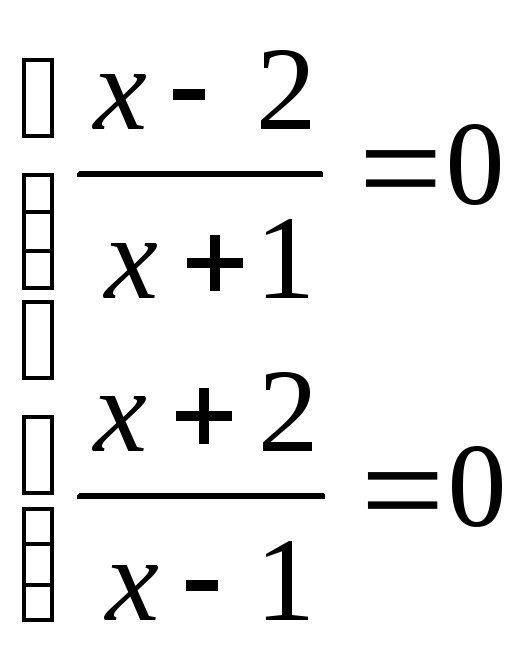
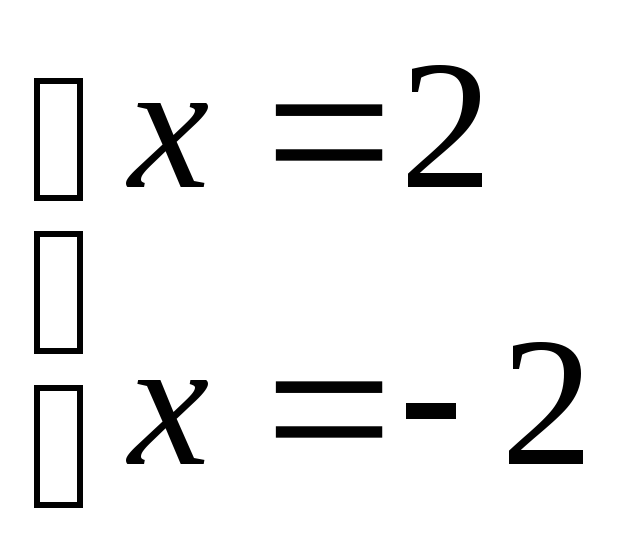решений нет

2) Разделим обе части уравнения на , получим

Решим последнее уравнение, как квадратное относительно , получим

;

;

Вернемся к замене.

или

корней нет

Ответ:

Пример №2.

Пусть , , тогда

Найдем

Составим систему:

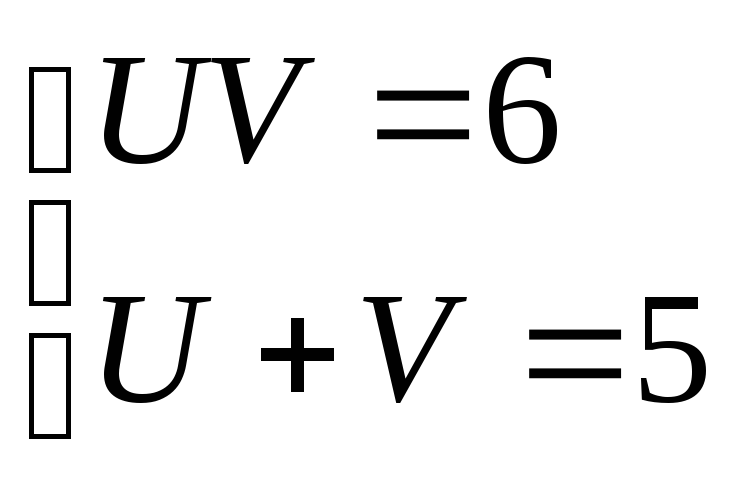
Решая систему подстановкой, получим

или

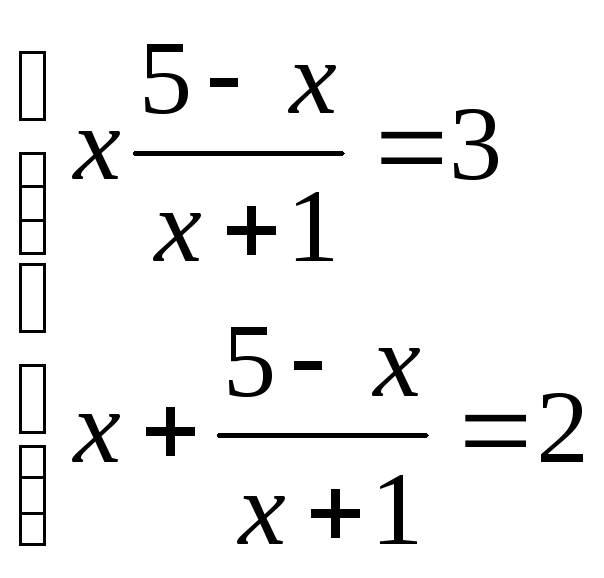
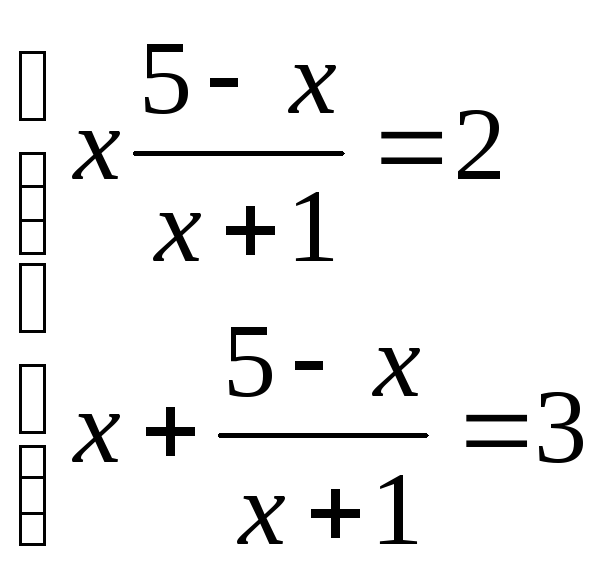
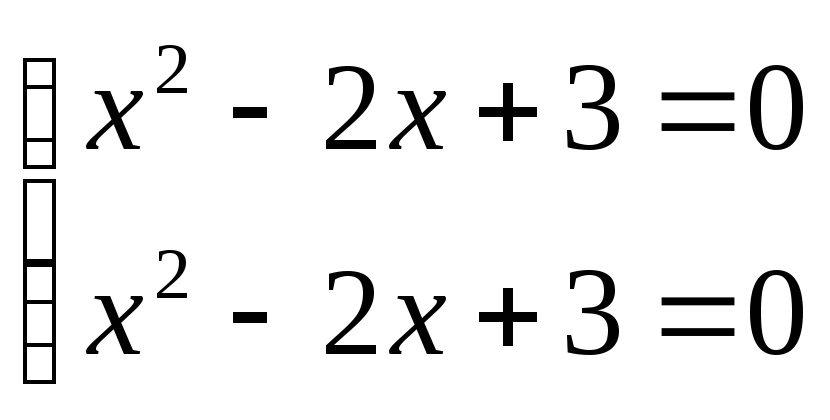
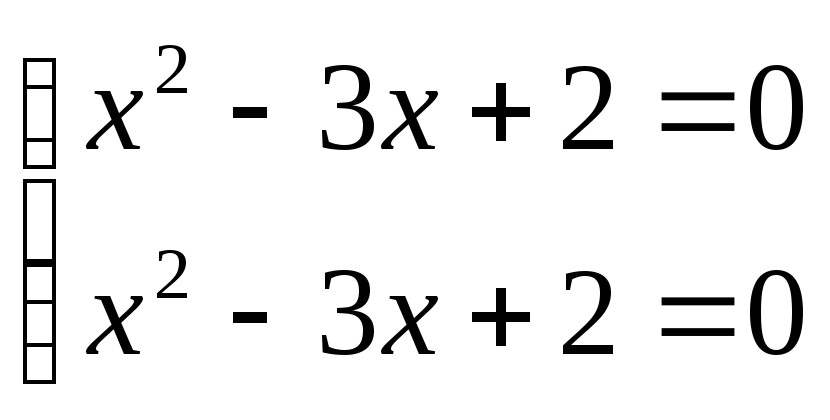
корней нет ;

Ответ: ;

Пример №3.

- не является корнем уравнения

Разделим обе части уравнения на , получим

Введем замену.

Пусть , тогда

;

или

; ;

Ответ: ; ; ;

VI) Уравнения вида, где эффективно решать перемножением и , а затем делать замену.

VII) В уравнениях вида и в уравнениях к ним сводящимся, в знаменателях обоих дробей необходимо вынести х за скобки и сделать замену.

(1)

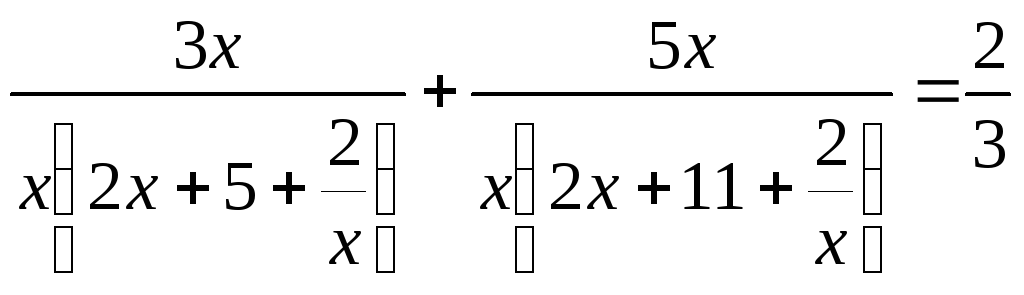(2)

При переходе область определения уравнения сузилась на . Проверим, является ли корнем уравнения. Не является.

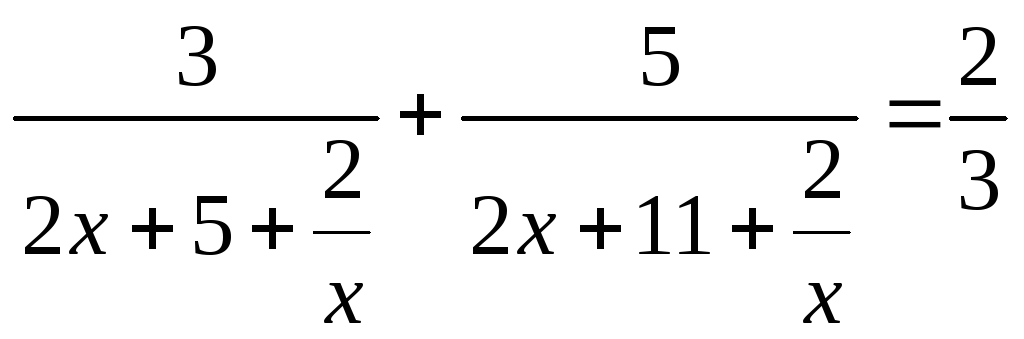
Введем замену.

Пусть , , тогда

;

или

Ответ: ;

VIII) В уравнениях вида обе части уравнения делятся на

- не является корнем уравнения. Разделим на , получим

Введем замену.

Пусть ; , тогда

;

или

Ответ: ;

IX) Выделение полного квадрата.

Введем замену.

Пусть , тогда

;

Вернемся к замене.

или

корней нет

Ответ:

X) Решение уравнений с помощью формулы

или

корней нет

XI) Уравнения вида и к ним сводящиеся решаются при помощи замены

Введем замену.

Пусть , тогда

или корней нет

;

Вернемся к замене.

или

Ответ: ;

XII) Решение уравнений относительно коэффициентов.

или

; - посторонний корень

корней нет

Ответ: ;

XIII) Метод разложения на простейшие дроби.

Ответ: