Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Вабищевич_Физика_ч

.1.pdf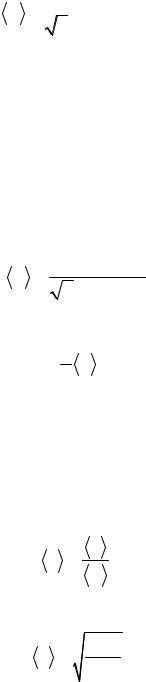

Скачиваний:

318

Добавлен:

18.05.2015

Размер:

1.9 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2021 / 2421 22 23 24 > Следующая >>>

2.4. Примеры решения задач

Пример 1.

Определите: 1) среднюю длину свободного пробега молекул; 2) число соударений за 1 с, происходящих между всеми молекулами кислорода, находящегося в сосуде емкостью 2 л при температуре 27°С и давлении 100 кПа.

Решение. Средняя длина свободного пробега молекул кислорода вычисляетсяпоформуле

λ =	1	,	(1)
	2 π d 2 n
	0

где d = 2,9 10-10 м – эффективный диаметр молекулы кислорода; n0 – число молекул в единице объема, которое можно определить по уравнению p = n0kT .

Число молекул равно

n =	p	,	(2)

0	kT

где k =1,38 10−23 Дж/К – постоянная Больцмана. Подставляя (2) в (1), имеем

	kT
λ =	2 π d 2 p .	(3)

Число соударений z, происходящих между всеми молекулами за 1 с

z =	1	z N ,	(4)
	2

где N – число молекул кислорода в сосуде объемом 2 10-3 м3; <z> – среднее число соударений одной молекулы за 1 с.

Число молекул в сосуде

N = n0V .			(5)
Среднее число соударений молекул за 1 с
z =	v ,		(6)
	λ
где <v> – средняя арифметическая скорость молекулы. Она равна
v =	8RT	,	(7)
	πµ

где µ = 32 10-3 кг/моль – молярная масса кислорода.

201

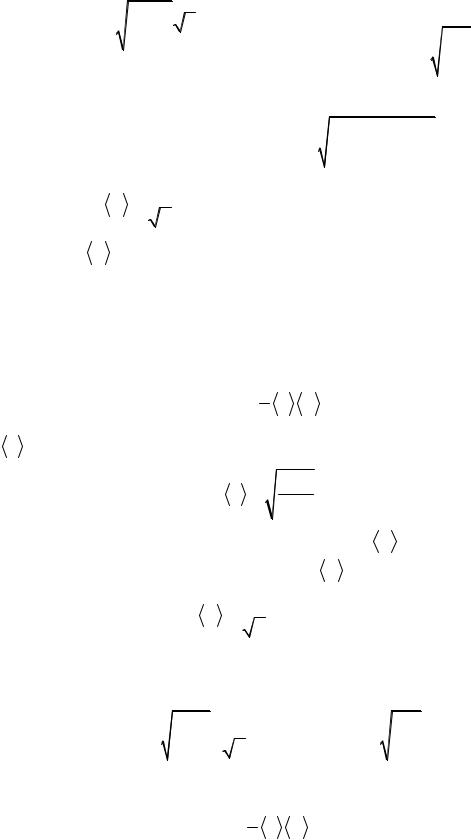
Подставляя в (4) выражения (5), (6) и (7), находим:

		8RT	2 πd 2 p	p		2πd 2 p2V	RT .
z =	1	πµ			V =
	2		kT	kT		k2T 2
							πµ

Выразим все величины в системе СИ и произведем вычисления:

z =	2 3,14 2,92 10−20 1010 2 10−3								8,31 300		= 9 1028 ;
	1,382 10−46 9		104					3,41 32		10−3

	λ =	1,38 10−23 300							= 3,56	10−8 .
		3,14	2,9	2	10	−20	10	5
	2

Ответ: λ = 3,56 10−8 м, z = 9 1028.

Пример 2.

Определите: 1) коэффициент диффузии; 2) коэффициент внутреннего трения азота, находящегося при температуре 300 К и давлении 105 Па.

Решение. Коэффициент диффузии
D = 1		v λ ,		(1)
	3
где v – средняя арифметическая скорость молекул, равная
v	=	8RT ,		(2)
		πµ
где µ = 28 10-3 кг/моль – молярная масса азота;				λ – средняя длина сво-
бодного пробега молекул. Для нахождения λ			воспользуемся формулой
λ =		kT	,	(3)
	2 πd 2 p

где k =1,38 10−23 Дж/К – постоянная Больцмана; d = 3,1 10-10 м – эффективный диаметр молекулы азота. Подставляя (2) и (3) в (1), имеем

D =

8RT

2kT

RT .

πµ

p 3

Коэффициент внутреннего трения

η=

λ ρ,

где ρ – плотность газа при температуре 300 К и давлении 105 Па.

202

Для нахождения ρ воспользуемся уравнением состояния идеального газа. Запишем его для двух состояний азота: при нормальных условиях

(Т0 = 273 К; р0 = 1,01 105 Па):


p V = m RT ,						и	pV = m RT .
0	0	µ			0		µ
Учитывая, что ρ0	=		m	; ρ = m		, мы имеем
Учитывая, что ρ0	=			; ρ = m		, мы имеем
		V0			µ

ρ = ρ0 pT0 . p0T

Коэффициент внутреннего трения газа может быть выражен через коэффициент диффузии

η = Dρ = Dρ0 pT0 . p0T

Выразим величины в системе СИ и проведем вычисления:

D =		2 1,38 10−23 300							8,31 300			= 4,7 10−5	;
D =			2	10	−20		10	5	3,14 28	10	−3	= 4,7 10−5	;
3		3,14 3,1		10			10		3,14 28	10
	η = 4,7 10−5 1,25							105 273		= 5,23 10−5 .
	η = 4,7 10−5 1,25									= 5,23 10−5 .
							1,01 105 300
Ответ: η = 5,23 10			−5	кг		.
Ответ: η = 5,23 10				м с		.
				м с

Пример 3.

Два тонкостенных коаксиальных цилиндра длиной 10 см могут свободно вращаться вокруг их общей оси Z. Радиус R большого цилиндра равен 5 см. Между цилиндрами имеется зазор размером d = 2 мм. Оба цилиндра находятся в воздухе при нормальных условиях. Внутренний цилиндр приводят во вращение с постоянной частотой n1 = 20 с-1. Внешний цилиндр заторможен. Определить, через какой промежуток времени с момента освобождения внешнего цилиндра он приобретет частоту вращения n2 = 1 c-1. При расчетах изменением относительной скорости цилиндров пренебречь. Масса m внешнего цилиндра равна 100 г.

Решение. При вращении внутреннего цилиндра слой воздуха увлекается им и начинает участвовать во вращательном движении. Вблизи поверхности этого цилиндра слой воздуха приобретает со временем практически

203

такую же линейную скорость, как и скорость точек на поверхности цилиндра, т.е. v = 2πn1 ( R − d ) . Так как R > d , то приближенно можно считать

v ≈ 2 πn1 R .

(1)

Вследствие внутреннего трения момент импульса передается соседним слоям газа и, в конечном счете, внешнему цилиндру. За интервал времени ∆t внешний цилиндр приобретает момент импульса L = p R, где р – импульс, полученный внешним цилиндром. Отсюда

p =		L	.	(2)

С другой стороны		R
	dv
p =η		S ∆t ,		(3)
	dz

где η – динамическая вязкость; dv/dz – градиент скорости; S – площадь

поверхности цилиндра ( S = 2π Rλ).
Приравняв правые части выражений (2)				и (3) и выразив из получен-
ного равенства искомый интервал ∆t, получим
∆t =	L		.	(4)
	η R dv
		S
	dz

Найдем входящие в эту формулу величины L, dv/dz, S. Момент импульса L = J ω, где J – момент инерции цилиндра (J = mR2); m – его масса; ω2 – угловая скорость внешнего цилиндра (ω2 = 2πn2). С учетом этого запишем

L = mR2 2π n = 2π mR2n .
2		2
Градиент скорости dv/dz = v/z =		v/d. Площадь цилиндра		равна
S = 2 πRλ . Подставив в (4) выражения L, dv/dz, S, получим:
∆t = m d n2 .
	η v λ
Заменив здесь v по (1), найдем
∆t =	m d n2
			.	(5)
	2 π η R λ n
		1

Динамическая вязкость воздуха η = 17,2 мкПа с = 1,72 10–5 Па с. Подставив в (5) значения входящих в формулу величин и произведя

вычисления, получим

∆t = 18,5 с.

Ответ: ∆t = 18,5 с.

204

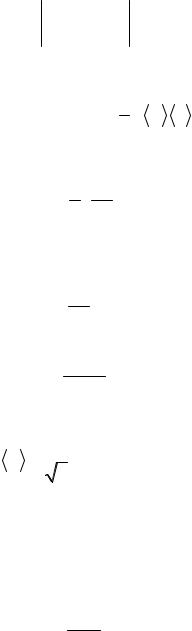
Пример 4.

Пространство между двумя параллельными пластинами площадью 150 см2 каждая, находящимися на расстоянии 5 мм друг от друга, заполнено кислородом. Одна пластина поддерживается при температуре 17°С, другая – при температуре 27°С. Определите количество теплоты, прошедшее за 5 мин посредством теплопроводности от одной пластины к другой. Кислород находится при нормальных условиях.

Эффективный диаметр молекул кислорода считать равным 0,36 нм. Решение. Количество теплоты, перенесенное газом в результате тепло-

проводности от одной пластины к другой

Q = χ ∆∆Tx S t ,

где χ – коэффициент теплопроводности.

∆T = tD	−tD ;	χ = 1 ρ λ v .
2	1	3
		3

СV – удельная теплоемкость газа при постоянном объеме

CV = 2i MR ,

где i – число степеней свободы (для кислорода i = 5); ρ = m/V – плотность. Используем уравнение Менделеева – Клапейрона

pV = Mm RT ,

откуда

ρ = pR MT .

Средняя длина свободного пробега молекул газа

λ =	1	,
	2 π d 2 n

где n – концентрация газа.

Уравнение состояния идеального газа p = n k T ,

откуда

n = k pT .

205

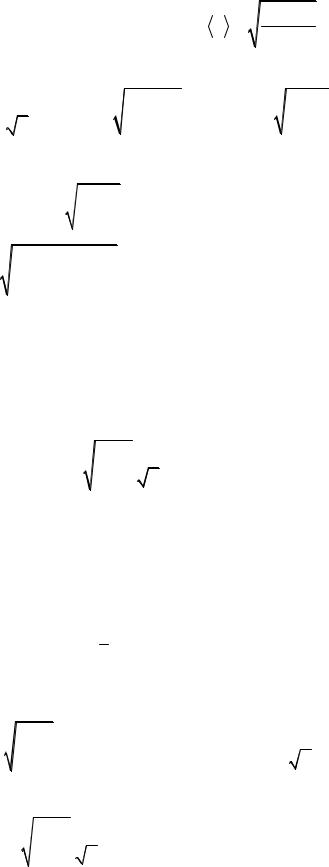
Средняя арифметическая скорость молекулы

8 R T .

π M

Тогда

χ = 1

R p M

k T

8 R T =

2 π d 2 p

π d 2

M R T

π M

Подставим это выражение в формулу количества теплоты:

(tD

−tD)

Q =

t ;

π d 2

π M

∆x

Q =

1,38 10−23

8,31 273

27 −17

15 10−3 300 = 76,4 (Дж) .

3,14 (3,6 10−10 )2

3,14 32 10−3

5 10−3

Ответ: Q = 76,4 Дж.

Пример 5.

Найти зависимость коэффициента диффузии от температуры при постоянномдавлении.

D =	1	υ		=	1	8RT	kT	.
			λ
	3				3
						πµ 2πσ2 p

Поэтомузависимостьимеетвид D = AT 32 припостоянномдавлениир.

Пример 6.

Найти зависимость коэффициента теплопроводности от температуры. Решение. Поскольку

χ= 13 υλСV ρ,

акаждая из величин определяется как

ρ =

pµ

;

υ =

8RT ;

C =

R ;

πµ

2µ

2πσ2 p

то подставив выражение

χ =

8RT RT pµ υ

R ,

πµ

2πυ2 p RT 2µ

получим

206

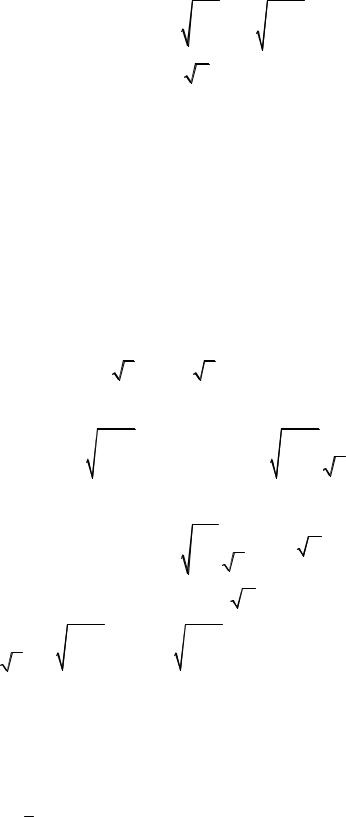
χ =	1	µ k	T	,

	3	πR πυ2	πµR

т.е. зависимость имеет вид χ = A T .

Пример 7.

Найти зависимость коэффициента внутреннего трения от температуры.

Решение. Поскольку η = 1 υ

λρ,

то согласно уравнению Менделеева – Клапейрона

pV = m RT ;

pµ

=ρ.

Длина пробега при этом может быть представлена в идее

λ =

, где p = nkT ,

2πυ2n

2πσ2 p

тогда

υ =

8RT ;

η = 1

pµ

8RT

πµ

3 RT

πµ 2πσ2 p

Окончательно получаем

η =

1 k 8R µ

= A T ;

3 R

πµ

σ2

η = A T ,

где A = 1

8µ

3πυ

2πσ2 π R

π R

Пример 8.

Найти коэффициент теплопроводности водорода, если известно, что коэффициент вязкости (внутреннего трения) для него при этих условиях

равен 8,6 10-6 нсек/м2.

η = 1 υ

λρ; χ = 1 υ

С ρ;

C =

; υ

3ηC

η R ;

λρ = 3η; χ =

2 µ

−6

−8

= 0,09 Вт/мК.

χ = 2 86 10

8,31

= 90 10

= 9

207

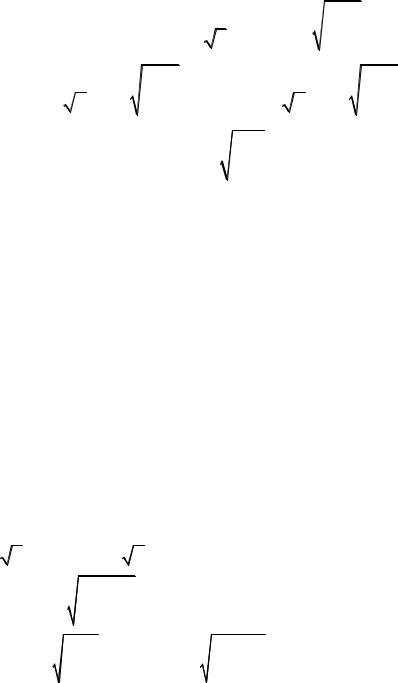
Пример 9.

Определите, во сколько раз отличается коэффициент динамической вязкости η углекислого газа и азота, если оба газа находятся при одинаковых условиях.

η = 1

pµ

; λ =

; υ =

8RT

;

λρ; ρ =

πµ

2πσ2 p

η1

1 pµ1

8RT

; η2

1 pµ2

8RT

;

3 RT

2πσ12 p

πµ1

2πσ22 p

πµ2

σ2

η2

µ2

σ12

Пример 10.

Цилиндрический термос с внешним радиусом r2 = 10 см и внутренним r1 = 9 см, высотой 20 см наполнен льдом. Температура льда 0° С, наружная температура 20° С.

1). При каком предельном давлении воздуха между стенками термоса коэффициент теплопроводности будет зависеть от давления? Температуру воздуха считать 10° С, диаметр молекул воздуха 3 10-10 м, µ = 29 г/моль.

2). Найти коэффициент теплопроводности воздуха при давлении:

а) 760 мм. рт. ст.;

б) 10–4 мм. рт. ст.

3). Какое количество тепла проходит за 1 мин через боковую поверх-

ность термоса средним радиусом 9,5 см за счет теплопроводности

а) 760 мм рт. ст.;

б) 104 мм рт. ст.

При

= d коэффициент теплопроводности начинает зависеть от

давления

p =

, p

= 7,37 10−3 мм рт. ст.

2πυ2 p

2πυ2d

а) χ = 1

С ρ =

и χ =13,1 10−6

Вт

;

πυ2

π µ

м К

б) χ= 1 dυρ C

= 1 d

8RT

pµ

=1,78 10−4

Вт

µ RT 2µ 6

π µ T

м К

Q = χ

∆T

∆S∆t, но ∆S = 2π rλ,

где r

r1 + r2

, Q = χ ∆T 2π rλ ∆t ;

∆x

∆T

тогда с учетом 2) получаем

б) Q2 = 2,55 Дж.

а) Q1 = 188 Дж;

208

3. УЧЕБНЫЙ БЛОК «ТЕРМОДИНАМИКА. АГРЕГАТНОЕ СОСТОЯНИЕ ВЕЩЕСТВА»

Введение

Раздел механики, в котором изучается законы движения жидкости и ее взаимодействия с телами, обтекаемыми средой, называется гидродинамикой. При изучении движения жидкости рассматривают ее как сплошную среду, отвлекаясь от молекулярного строения жидкости. В ряде случаев пренебрегают внутренним трением и рассматривают модель идеальной жидкости.

При изучении данного раздела студенты должны

иметь представление:

–об основных физических величинах: давлении, работе, кинетической и потенциальной энергии;

–об основных законах гидростатики: законе Архимеда, законе Паскаля. Знание гидростатического давления;

обладать навыками:

–примененияэлементовдифференциальногоиинтегральногоисчисления.

Учебная программа блока

Содержание программы	Форма	Литература
	подготовки
1. Первое начало термодинамики. Работа. Внут-		[2, § 9.1	– 9.3],
ренняя энергия. Теплота	лекция	[5, § 82 – 84],
		[6, § 14, 15]
2. Применение первого начала термодинамики к		[2, § 9.5	– 9.6],
изопроцессам. Зависимость теплоемкости иде-		[2, § 9.5	– 9.6],
изопроцессам. Зависимость теплоемкости иде-	лекция	[5, § 87	– 90],
ального газа от вида процесса. Адиабатный про-	лекция	[5, § 87	– 90],
ального газа от вида процесса. Адиабатный про-		[6, § 21]
цесс. Политропный процесс		[6, § 21]
цесс. Политропный процесс
3. Обратимые и необратимые процессы. Круговой		[2, § 11.1	– 11.2],
процесс (цикл). Цикл Карно	лекция	[5, § 105],
		[6, § 29 – 30]
4. Энтропия. Второе начало термодинамики. Вы-
числение энтропии идеального газа.	лекция	[2, § 11.3	– 11.6],
Статистическое толкование второго начала тер-	лекция	[5, § 104, 107]
Статистическое толкование второго начала тер-		[5, § 104, 107]
модинамики
5. Отступления от законов идеальных газов. Ре-		[2, § 12.1	– 12.3],
альные газы. Уравнение Ван-дер-Ваальса	лекция	[5, § 91],
		[6, § 97 – 98]

209

		Окончание табл.
6. Фазовые переходы I и II рода. Критическое со-		[2, § 12.3],
стояние.	лекция	[5, § 120, 123],
Уравнение Клапейрона – Клаузиуса		[6, § 111, 113]
7. Поверхностное натяжение. Формула Лапласа.	самост.	[5, § 115 – 119],
Капиллярные явления		[6, § 106 – 109]

Цели обучения

студент должен знать	студент должен уметь
– определения теплоты, внутренней энергии и работы	– вычислять изменение внут-
газа;	ренней энергии, работу газа и
– связь параметров состояния при различных про-	количество теплоты в различ-
цессах;	ных процессах;
– первый закон термодинамики. Смысл величин,	– определять КПД различных
входящих в него;	круговых процессов;
– понятие теплоемкости для различных процессов;	– вычислять изменение энтро-
– политропический процесс;	пии;
– КПД тепловых машин;	– находить связь критических
– цикл Карно;	параметров вещества и попра-
– определение второго начала термодинамики;	вок в уравнении Ван-дер-
– способы вычисления энтропии идеального газа;	Ваальса;
– статистическое толкование второго начала термо-	– определять температуру фа-
динамики;	зового перехода;
– уравнение Ван-дер-Ваальса. Смысл поправок для	– определять работу сил по-
давления и объема;	верхностного натяжения, лап-
– фазовое состояние вещества. Фазовые переходы I	лассово давление
и II рода. Критическое состояние;
– уравнение Клапейрона – Клаузиуса;
– причины возникновения поверхностного натяже-
ния, добавочного давления над искривленной по-
верхностью

3.1. Краткое содержание теоретического материала

Физические свойства макросистем, состоящих из большого количества частиц, изучаются взаимно дополняющими методами: статистическим и термодинамическим. Термодинамический метод основан на анализе условий и количественных соотношений при различных превращениях энергии, происходящих в системе. Внутренняя энергия термодинамической системы включает в себя кинетическую энергию движения частиц (поступательного и вращательного движения), а также потенциальную энергию их взаимодействия. В идеальном газе пренебрегают силами межмолеку-

210

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2021 / 2421 22 23 24 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.05.20152.29 Mб179УМК ЭП.doc
#
29.08.20191.5 Mб49УМК_1!!!!!!!!!!!!!!!!.doc
#
18.05.20152.61 Mб107умк_Андреева.pdf
#
29.08.20191.27 Mб39умк_Боброва_Анг.яз_для экон._2010.doc
#
18.05.20151.91 Mб149умк_Вабищевич_квант. физики.pdf
#
18.05.20151.9 Mб318умк_Вабищевич_Физика_ч.1.pdf
#
18.05.20152.19 Mб191умк_Вабищевич_Физика_ч.2.pdf
#
18.05.20153.54 Mб144умк_Галушков_Неорган химия_для ХТ.pdf
#
18.05.20153.15 Mб50умк_Галушков_Теорет. основы химии_ч.1.pdf
#
18.05.20152.09 Mб85умк_Галушков_Теорет. основы химии_ч.2.pdf
#
18.05.20151.22 Mб82умк_Гарбуль_Англ для неязыковых спец.pdf