
умк_Вабищевич_Физика_ч
.1.pdfОкончание табл.
12. Двеформыуравненияколебаний |
углубление и систе- |
практическое занятие |
2 |
|
матизация навыков |
|
|
13. Виды колебаний. Сложение |
формирование новых |
лекция |
2 |
колебаний. Резонанс |
знаний |
|
|
14. Механика материальной точки |
формирование новых |
|
|
(по графику из списка лаборатор- |
знаний |
лабораторное занятие |
4 |
ных работ) |
|
|
|
15. Вынужденные и затухающие |
формирование новых |
практическое занятие |
1 |
колебания. Сложение колебаний |
знаний |
|
|
16. Механика материальной точки |
занятие-проверка ре- |
итоговое занятие |
1 |
|
зультатов обучения |
||
|
|
|
|
11
1. УЧЕБНЫЙ БЛОК «КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ»
Введение
Кинематика – раздел механики, в котором изучается движение тел, но не рассматриваются причины, вызывающие это движение. Любое сложное движение может быть представлено совокупностью простейших движений: поступательного, колебательного и вращательного. При поступательном и в ряде случаев колебательного движений формой и размерами тела можно пренебречь, так как от них не зависят закономерности движения. В этом случае тела заменяются их моделью – материальной точкой, т.е. объектом, не имеющим размеров, но обладающим массой. В настоящем учебном блоке рассматриваются закономерности поступательного движения, поэтому они рассматриваются с использованием модели материальной точки (м.т.).
Представление движущегося тела материальной точкой возможно только в случае, когда все его элементы движутся по одинаковым траекториям. Это является признаком (критерием) поступательного движения.
Для описания движения используются системы координат. Программа данного учебного блока предусматривает получение навыков использования прямоугольной (декартовой) и сферической систем координат. Критерием выбора той или иной системы координат являются наибольшая простота получаемых уравнений движения и наименьшее их количество.
Для успешного изучения учебного материала данного блока учащийся должен в рамках программы средней школы
иметь представление:
–об основных кинематических характеристиках движения;
обладать навыками:
–использования прямоугольной системы координат;
–сложения и вычитания векторов;
–дифференцирования и интегрирования простейших функций.
Учебная программа блока
Содержание блока |
Форма |
Литература |
|
подготовки |
|||
1. Система сферических и прямоугольных координат. |
лекция, |
[4] |
|
Связь систем координат |
самост. |
||
|
|||
2. Траектория, путь, перемещение, уравнение траектории |
самост. |
[3], [4] |
|
3. Скорость: средняя, мгновенная |
самост. |
[3] |
12
|
|
|
|
|
|
|
|
|
|
Окончание табл. |
|||
|
4. Ускорение: среднее, мгновенное |
|
|
|
самост. |
|
[3] |
|
|||||
|
5. Криволинейное движение. Угловая скорость и угловое |
|
самост., |
|
[3], [4] |
|
|||||||
|
ускорение. Нормальное, тангенциальное, полноеускорения |
|
лекция |
|
|
||||||||
|
|
|
|
|
|||||||||
|
6. Принцип относительности и суперпозиция движений. |
|
лекция |
|
[2], [3], [4] |
|
|||||||
|
Сложение скоростей иускорений |
|
|
|
|
|
|
|
|||||
|
Цели обучения |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||
|
|
студент должен знать |
|
|
студент должен уметь |
|
|
||||||
|
– способы задания положения мате- |
|
– определять координаты точки по ее радиус- |
||||||||||
|
риальной точки в декартовой и сфе- |
|
вектору; |
|
|
|
|
||||||
|
рической системах координат; |
|
– определять радиус-вектор точки по ее коор- |
||||||||||
|
– основные кинетические величины, |
|
динатам; |
|
|
|
|
||||||
|
характеризующие движение мате- |
|
– находить значение скорости и ускорения мате- |
||||||||||
|
риальной точки: траектория, пере- |
|
риальной точки по известной зависимости от |
||||||||||
|
мещение, пройденный путь, ско- |
|
времени еерадиус-вектора; |
|
|
||||||||
|
рость |
и ускорение |
материальной |
|
– рассчитывать величину перемещения и прой- |
||||||||
|
точки; |
|
|
|
|
|
денного пути; |
|
|
|
|
||
|
– основные кинематические вели- |
|
– получать уравнение траектории движения |
||||||||||
|
чины, |
характеризующие |
движение |
|
материальной точки; |
|
|
|
|
||||
|
материальной точки по окружности: |
|
– использовать принцип независимости дви- |
||||||||||
|
угловое перемещение, угловая ско- |
|
жений при решении задач по движению тела; |
||||||||||
|
рость, угловое ускорение; |
|
– находить тангенциальное, нормальное, пол- |
||||||||||
|
– связь между линейными и угловы- |
|
ное ускорения тела и радиус кривизны траек- |
||||||||||
|
ми кинематическими величинами; |
|
тории при криволинейном движении; |
||||||||||
|
– принципы |
относительности и |
|
– находить угловую скорость, угловое, нор- |
|||||||||
|
суперпозиции |
движений: |
сложение |
|
мальное, тангенциальное и полное ускорения |
||||||||
|
перемещений, скоростей, ускорений. |
|
при круговом движении по зависимости от |
||||||||||
|
|
|
|
|
|
|
времени угла поворота радиус-вектора |
||||||
|
1.1. Краткое содержание теоретического материала |
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||
|
Положение |
материальной |
точки |
|
|
|
|
|
|||||
в пространстве в данный момент времени |
|
|
|
|
|
||||||||
задается с использованием системы коор- |
|
|
|
|
|
||||||||
динат |
относительно |
некоторой |
точки |
|
|
|
|
|
|||||
(тела) отсчета, которая является началом |
|
|
|
|
|
||||||||
системы координат. Отрезок, соединяю- |
|
|
|
|
|
||||||||
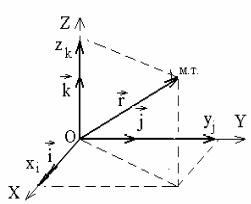
щий точку отсчета О (рис. 1.1) и матери- |
|
|
|
|
|
||||||||
альную |
точку (м.т.) и направленный |
|
|
|
|
|
|||||||
к м.т., |
называется |
радиус-вектором ( r ). |
|
|
|
|
|
||||||
|
Рис. 1.1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
13
Хотя rG определяет положение м.т., описать это положение с его помощью невозможно, т.к. для этого необходимо описать направление rG. Поэтому для описания положения м.т. используют системы координат, в частности прямоугольную (см. рис. 1.1). В этой системе проекции r на взаимноперпендикулярные оси координат x, y, z полностью определяют модуль и направление r
rG = xi + yjG + zk , |
(1) |
если выбраны (заданы) орты (единичные векторы) системы координат. В скалярной форме (1) запишется через координаты в виде
r = x2 + y2 + z2 . |
(2) |
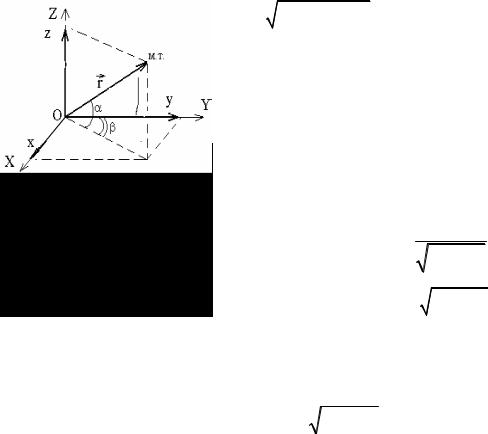
В ряде случаев, например – движения м.т. по сферической поверхности, удобно использовать сферическую систему координат, в которой параметрами являются модуль радиус-вектора – r, азимутальный угол – β и полярный угол – α (рис. 1.2).
При этом параметры прямоугольной и сферической систем координат связаны соотношением (2) и (3).
β = arccos |
x |
; |
(3) |
x2 + y2 |
|
α = arccos |
x2 |
+ y2 |
|
|
Рис. 1.2 |
|
r |
|||
|
|
|
|||
или |
|
|
|
|
|
|
z |
|
|
|
|
α = arccos |
|
. |
|
(4) |
|
x2 + y2 |
|
||||
Таким образом в любой выбранной системе координат достаточно трех параметров для описания положения материальной точки. Сферическая система координат в дальнейшем будет привлекаться только в тех случаях, где она более удобна, чем прямоугольная.
При движении материальной точки ее координаты и радиус-вектор изменяются со временем, а сама материальная точка (конец rG) описывает в пространстве линию, которая называется ее траекторией.
Законом движения или уравнением траектории в векторной форме
называется зависимость радиус-вектора материальной точки от времени
rG = rG(t) = x(t)i + y(t) Gj + z(t)k , |
(5) |
14
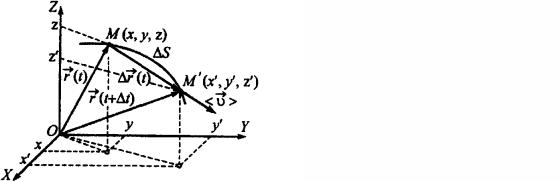
Это уравнение эквивалентно трем уравнениям для координат
x = x(t) ; |
y = y(t) ; z = z(t). |
(6) |
Для получения уравнения траектории материальной точки в явном виде из системы (6) необходимо исключить время t, т.е. получить зависимость координат друг от друга. По форме траектории бывают прямолинейными и криволинейными. Если при движении материальная точка находится все время в одной плоскости, то такое движение называется плоским. При этом можно использовать неполную систему координат, например хоу, хoz или zoy.
Вектор перемещения и отрезок пути материальной точки. Скаляр-
ную величину ∆S, равную расстоянию вдоль траектории, пройденному точкой за данный промежуток времени, называют отрезком пути материальной точки (путем). Путь положителен всегда и в процессе движения может только возрастать.
Пусть за время ∆t материальная точка переместилась из точки М в точку М*, пройдя вдоль траектории отрезок пути ∆S (рис. 1.3). Вектор ∆rG, проведенный из начальной точки М в конечную точку М*, называется вектором перемещения материальной точки за время ∆t
∆r = rG(t + ∆t) − rG(t) , |
|
или |
|
∆rG = ∆xi + ∆yjG + ∆zk , |
(7) |
где ∆x = x/ − x ; ∆y = y/ − y ; ∆z = z/ − z .
Из рис. 1.3 видно, что при криволинейном движении отрезок пути ∆S не равен величине вектора перемещения
∆rG |
|
= (∆x)2 + (∆y)2 + (∆z)2 . |
* |
|
Вектором средней скорости за время
∆t называется отношение вектора перемещения материальной точки ко времени, за
которое оно совершено
< υG >= ∆rG = ∆x iG + ∆y Gj + ∆z kG =< υx > iG+ < υ ∆t ∆t ∆t ∆t
Рис. 1.3 |
|
y > Gj + < υz > kG. |
(8) |
Направление вектора < υ > совпадает с ∆r (рис. 1.3), а абсолютная величина равна
15

G |
| ∆rG| |
= < υx > |
2 |
+ < υy > |
2 |
+ < υz > |
2 |
= |
|
∆x 2 |
|
∆y 2 |
|
∆z 2 |
|
|< υ >|= |
∆t |
|
|
|
|
|
+ |
|
+ |
|
. (9) |
||||
|
|
|
|
|
|
|
|
|
∆t |
|
∆t |
|
∆t |
|
|
Средней путевой скоростью за время ∆t называется отношение отрезка пути ∆S к ∆t:
υ |
= |
∆S . |
(10) |
ср |
|
∆t |
|
Средняя путевая скорость является скалярной величиной.
Так как ∆S = | ∆rG| только в случае движения с неизменной по направлению скоростью, то в общем случае средняя путевая скорость не совпадает с модулем вектора средней скорости: υср ≠|< υ >| .
Вектор скорости материальной точки υ(t) в данный момент времени t
определяется как предел, к которому стремится вектор средней скорости < υG > за время от t до t + ∆t при безграничном уменьшении промежутка времени ∆t
G |
G |
∆r |
G/ |
(t), |
υ(t) = lim |
< υ >= lim |
∆t |
= r |
|
∆t→0 |
∆t→0 |
|
|
где штрих означает производную по времени, которую принято записывать в виде
(11)
где drG – перемещение материальной точки за бесконечно малый промежуток времени dt . G
Заметим, что при ∆t → 0 вектор ∆r → dr и направлен в сторону движения по касательной к траектории материальной точки в момент времени t, а по абсолютной величине
|
drG |
|
|
|
|
|
|
|
|
|
|
|
| dr |= dS. |
|
|
|
|
|
|
|
|
|
|
(12) |
||
G |
= lim |
|
∆x G |
+ |
∆y |
G |
∆z G |
dx G |
|
dy G |
dz |
|
G |
G |
G |
G |
, (13) |
|||||||||
υ(t) = |
dt |
|
∆t |
i |
∆t |
j + |
∆t |
k = |
dt |
i + |
dt |
j + |
dt |
k |
= υxi |
+υy j |
+υzk |
|||||||||
|
∆t→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где проекции вектора скорости на оси декартовой системы координат |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
υx = dx , |
|
υy = dy , |
|
|
υz = dz |
, |
|
|
|
(14) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
dt |
|
|
|
|
dt |
|
|
|
|
|
|
|
а модуль вектора скорости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
υ = |
|
G |
|
= |
|
2 |
2 |
|
2 |
dx |
2 |
|
dy 2 |
dz |
2 |
|
(15) |
|||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
υ |
|
υx + υy |
+ υz = |
|
|
|
|
+ |
|
|
|
+ |
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
dt |
|
|
dt |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
16
Таким образом вектор скорости материальной точки υG(t) направлен
по касательной к траектории в сторону движения, его проекции на оси OX, OY, OZ определяются соотношениями (14), а абсолютная величина – выражением (15).
Модуль вектора скорости (используя (12)) также можно определить с помощью выражения
|
G |
|
|
|
dr |
|
|
dS |
, |
(16) |
|
|
|
|
|||||||
υ = |
υ |
|
= |
|
|
|
= |
dt |
||
|
|
|||||||||
|
|
dt |
|
|||||||
|
|
|
|
|
|
|
|
|
т.е., взяв производную от пути по времени.
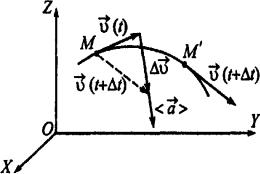
Пусть материальная точка, перемещаясь по своей траектории (рис. 1.4), находилась в момент времени t в точке М, а в момент времени t + ∆t –
в точке |
М*. |
Векторы скорости υ(t) |
|
|
|
|
|
|
|||
G |
|
* |
|
|
|
и υ(t + ∆t) в точках М и М направлены |
|
|
|||
по касательным к траектории. Если дви- |
|
|
|||
жение материальной точки криволиней- |
|
|
|||
ное, то, |
очевидно, направления υ(t) и |
|
|
||
G |
Gне совпадают. Перенесем начало |
|
|
||
υ(t + ∆t) |
|
|
|||
вектора υ(t + ∆t) , не изменяя его направ- |
|
|
|||
ления, в точкуGМ и соединим вектором ∆υ |
|
|
|
||
|
|
Рис. 1.4 |
|||
конец вектора |
υ(t) сконцомперенесенного |
|
|||
G |
|
|
|
|
|
вектора υ(t + ∆t) |
|
G |
|
||
|
|
G |
|
(17) |
|
|
|
∆υ = υ(t + ∆t) |
− υ(t). |
||
Вектором среднего ускорения за время ∆t называют отношение приращения вектора скорости ∆υ ко времени, за которое оно совершено
G |
|
∆υ |
|
< a |
>= |
∆t . |
(18) |
G |
|
|
G |
Направление вектора <a> совпадает с направлением ∆υ (см. рис. 1.4).
Выражение (18) при ∆t, стремящемся к нулю, определяет вектор ускорения материальной точки в момент времени t (мгновенное ускорение)
|
|
|
|
|
G |
|
|
∆υ |
|
|
G/ |
|
|
G |
|
|
|
||
|
|
|
|
|
= lim |
|
|
(t ) = |
d υ |
, |
|
(19) |
|||||||
|
|
|
|
|
a |
∆t |
|
= υ |
|
dt |
|
||||||||
G |
|
|
|
|
|
∆t →0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где dυ – приращение вектора скорости за бесконечно малый промежуток |
|||||||||||||||||||
времени dt. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выражение (19) можно записать в виде |
|
|
|
|
|
||||||||||||||
G |
|
d υ |
x |
G |
|
d υy |
G |
|
d υ |
z |
G |
|
G |
|
G |
G |
(20) |
||
a |
= |
|
i |
+ |
|
j |
+ |
|
|
|
k |
= axi |
+ ay j |
+ az k . |
|||||
dt |
|
dt |
|
dt |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
17

Следовательно, проекции вектора ускорения на координатные оси
ax = |
dυ |
x |
; |
ay = |
dυy |
; |
az = |
dυ |
z |
, |
dt |
|
dt |
dt |
|
||||||
|
|
|
|
|
|
|
|
а модуль вектора ускорения
|
|
G |
|
2 |
2 |
2 |
|
dυ |
x |
2 |
dυy 2 |
dυ |
z |
2 |
||||
|
|
|
||||||||||||||||
a = |
|
a |
= |
ax |
+ ay |
+ az |
= |
|
|
|
+ |
|
|
+ |
|
. |
||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
dt |
|
dt |
|
|
|
(21)
(22)
Следует отметить, что понятие, аналогичное υср (10), для ускорения не используется. Если речь идет о среднем ускорении, то имеется в виду
вектор среднего ускорения < a > (18).
Если траекторияG материальной точки лежит в плоскости XOY, то вектор ускорения a всегда можно разложить на две взаимно перпендикулярные составляющие (рис. 1.5)
(23)
где aGn – нормальное (или центростремительное) и aτ – тангенциальное (или касательное) ускорения материальной точки. Вектор aGn всегда направлен к центру кривизны траектории 0' в точке М, а вектор aGτ лежит на
касательной к траектории в точке М и может быть направлен как в сторону движения, так и в противоположнуюGсторону. Такое разложение вектора ускорения a часто необходимо в связи с тем, что вектор скорости материальной точки υ может изменяться как по направлению, так и по абсолютной величине. Нормальное ускорение an характеризует быстроту изменения
Рис. 1.5
an = aGn и aτ =
направления вектора скорости материальной точки. Тангенциальное ускорение aτ характеризует быстро-
туизменениямодуляскоростиматериальнойточки. Можно показать, что абсолютные значения
aGτ определяются соотношениями
a |
= |
υ2 |
(24) |
|
; |
||||
n |
|
R |
|
|
|
|
|
||
a |
= |
dυ |
, |
(25) |
|
||||
τ |
|
dt |
|
|
где υ = υG – модуль скорости материальной точки; R – радиус кривизны
траектории в данный момент времени.
18
Из (24) – (25) видно, что an ≥ 0 (причем an = 0 при прямолинейном движении: R → ∞), aτ > 0 при ускоренном движении материальной точки, aτ < 0 , если материальная точка движется замедленно, и aτ = 0 при равно-
мерном движении.
Из (23) и рис. 1.5 следует, что абсолютные значения величин a, an , aτ связаны между собой соотношением
a = |
|
aG |
|
= a2 |
+ a2 . |
(26) |
|
|
|||||
|
|
|
|
n |
τ |
|
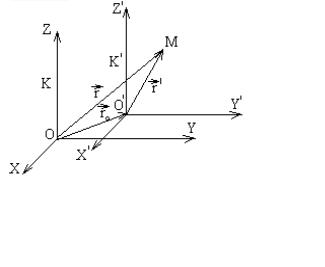
Понятия скорости и ускорения являются относительными и зависят от выбора системы координат. Пусть имеется неподвижная система отсчета
К и система отсчета К/, движущаяся посту- |
|
|
|
||
|
|
|
|||
пательно (углы между осями ОХ и О'Х', OY и |
|
|
|
||
O'Y/, 0Z и O'Z' остаются все время постоян- |
|
|
|
||
ными) относительно К (рис. 1.6). |
М |
|
|
|
|
Положение |
материальной точки |
|
|
|
|
в системах отсчета К и К' в один и тот же |
|
|
|
||
момент времени определяется радиус- |
|
|
|
||
векторами rG и rG/ |
соответственно. Из рис. 1.6 |
|
|
|
|
|
Рис. 1.6 |
|
|||
видно, что |
|
|
|
|
|
rG = rG + rG/ , |
|
|
|
|
|
|
|
(27) |
|||
|
0 |
|
|
|
|
где rG0 – радиус-вектор начала координат О' системы К' в системе К. Взяв производную по времени от левой и правой частей уравнения (27), получим
drG |
drG |
drG/ |
или |
G G G/ |
, |
(28) |
= |
0 + |
|
υ= υ + υ |
|||
dt |
dt |
dt |
|
0 |
|
|
где υG– скорость материальной точки относительно неподвижной системы
отсчета К; υG/ – скорость материальной точки относительно движущейся системы отсчета К/ – относительная скорость, υ0 – скорость поступа-
тельного движения системы отсчета К' относительно системы К – пере-
носная скорость.
Продифференцировав (28) еще раз по времени, получим
|
G |
|
G |
|
G |
/ |
|
|
|
|
|
dυ |
= |
dυ0 |
+ |
dυ |
|
или aG = aG |
|
+ aG/ , |
(29) |
|
|
|
|
|
|
|||||
|
dt |
|
dt |
|
dt |
0 |
|
|
||
|
|
|
|
|
|
|
|
|||
где aG – ускорение материальной точки в системе К; aG/ |
– ее ускорение в |
|||||||||
системе К/, aG |
– ускорение системы отсчета К' |
относительно К. Соотноше- |
||||||||
0 |
|
|
|
|
|
|
|
|
|
|
ние (28) представляет собой правило сложения скоростей.
19
Из полученных правил сложения скоростей (28) и ускорений (29),
в частности, следует, что если материальная точка участвует в нескольких |
|||||
G G |
G |
|
G |
G |
то резуль- |
движениях со скоростями, υ1, υ2 |
, υ3,... и ускорениями a1,a2 |
, a3,..., |
|||
G |
|
a материальной точки относительно |
|||
тирующие скорость υ и ускорение |
|||||
неподвижной системы отсчета К определяются выражениями |
|
||||
|
G |
G |
+... ; |
|
(30) |
υ1 + υ2 |
+ υ3 |
|
|||
a + aG |
+ aG |
+... . |
|
(31) |
|
1 |
2 |
3 |
|
|
|
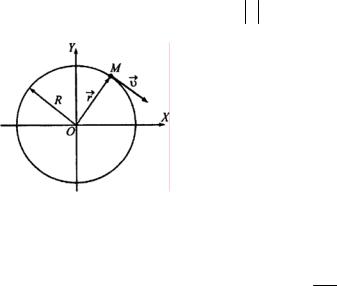
Кинематика движения материальной точки по окружности
Пусть материальная точка совершает движение по окружности радиусом R. Выберем систему координат, плоскость XOY которой совпадает
сплоскостью движения материальной точки, а начало координат совпадает
сцентром окружности, описываемой материальной точкой (рис. 1.7). Ско-
рость движения материальной точки υ, направленная по касательной к траектории, всегда перпендикулярна радиус-вектору материальной точки rG, а величина радиус-вектора r = R не меняется со временем.
При движении материальной точки по окружности, кроме скорости υ, которую часто называют линейной скоростью, удобно использовать поня-
тие угловой скорости материальной точки ω.
Средней угловой скоростью <ω> материальной точки на данном участке движения называется величина, равная отношению угла поворота ∆ϕ
Рис. 1.7 радиус-вектора точки за некоторый промежуток времени ∆t к этому промежутку времени:
<ω>= ∆∆ϕt ,
аугловую скорость ω определим, как предел, к которому стремится <ω> при ∆t → 0:
ω= lim |
< ω>= lim |
∆ϕ |
= dϕ |
, |
(32) |
∆t→0 |
∆t→0 |
∆t |
dt |
|
|
где dϕ – угол, на который поворачивается радиус-вектор материальной точки rG за бесконечно малый промежуток времени dt.
20
