6.10. Правило эквивалентности прямой последовательности

Обращаясь к полученным выражениям для симметричных составляющих токов и напряжений в месте несимметричного КЗ (табл. 6.3), замечаем, что токи и напряжения обратной и нулевой последовательностей пропорциональны току прямой последовательности в месте КЗ. Следовательно, задача расчета любого несимметричного КЗ прежде всего состоит в нахождении тока прямой последовательности в месте рассматриваемого вида КЗ.

Величина тока прямой последовательности определяется так:

- при двухфазном КЗ (6.18):

;

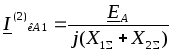- при однофазном КЗ (6.24):

;

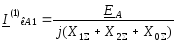- при двухфазном КЗ на землю (6.29):

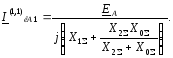
Структура приведенных выражений позволяет ток прямой последовательности особой фазы (А) при любом (n) виде несимметричного КЗ выразить в общем виде:

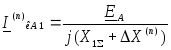, (6.34)

где ΔХ⁽ⁿ⁾ – дополнительная реактивность, величина которой для каждого вида КЗ определяется только значениям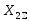и и.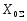

Кроме того, согласно выражениям (6.15), (6.20), (6.30), абсолютная величина полного тока поврежденных фаз в месте КЗ пропорциональна току прямой последовательности, что позволяет записать общее выражение:

,

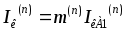где m⁽ⁿ⁾ – коэффициент пропорциональности, зависящий от вида КЗ.

Значения ΔХ⁽ⁿ⁾ и m⁽ⁿ⁾ для различных видов КЗ приведены в табл. 6.3.

• Таблица 6.3

  Определяемая величина	Виды КЗ
  	К(2)	К(1)	К(1,1)
  Токи в месте КЗ а. Прямой последовательности в фазе А IкА1 б. Обратной последовательности в фазе А IкА2 в. Нулевой последовательности IкА 0	ЕА / j(Х1+Х2) -IкА1 0	ЕА / j(Х1+Х2+Х0) IкА1 IкА1	ЕА / j(X1+Х2║Х0) -IкА1Х0/(Х0+Х2) IкА1Х2/(Х0+Х2)
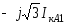
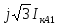
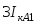
  Полный ток КЗ а. В фазе А IкА б. В фазе В IкВ в. В фазе С IкС	0	0 0	0 IкА1 ((a²-(Х2+аХ0) / (Х2+Х0)) IкА1 ((а-(Х2+а2Х0) / (Х2+Х0))
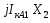
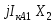
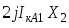
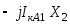
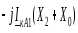
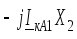
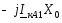
  Напряжения в месте КЗ а. Прямой последовательности UкА1 б. Обратной последовательности UкА2 в. Нулевой последовательности UкА0 г, Фазы А UкА д. Фазы В UкВ е. Фазы С UкС	0	0 IкА1j[(а²-а) Х2+(а²-1)Хо] IкА1j[(а-а²) Х2+(а-1)Хо]	jIкА1 Х2׀׀Х0 jI кA1 Х2 ׀׀Х0 jIкА1 Х2׀׀Х0 3jIкА1Х2׀׀Х0 0 0
  Дополнительное сопротивление ΔХ(n)	Х2	Х2+Х0	Х2//Х0
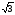
  Коэффициент m(n)		3

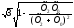
Обобщенная запись выражения (6.34) позволила Н.Н. Щедрину впервые сформулировать важное положение, которое называют правилом эквивалентности прямой последовательности.

Ток прямой последовательности любого несимметричного КЗ может быть определен как ток при трехфазном КЗ в точке, удаленной от действительной точки КЗ на дополнительное сопротивление ΔХ⁽ⁿ⁾, которое не зависит от параметров схемы прямой последовательности и для каждого вида КЗ определяется результирующими сопротивлениями обратной последовательности Х_2Σ и нулевой последовательности Х_0Σ относительно рассматриваемой точки схемы.

Сопоставляя множители перед током 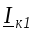в выражениях для напряжения прямой последовательности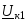со значениями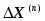можно записать в общем виде:

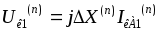
. (6.35)

Установленная идентичность между токами прямой последовательности (табл. 6.3) несимметричного КЗ и током при некотором эквивалентном трехфазном КЗ указывает, что все полученные ранее выражения для тока трехфазного КЗ и практические методы его расчета можно распространить на случаи несимметричных КЗ, т. е. для расчета последних не нужно создавать какие-либо специальные методы.