
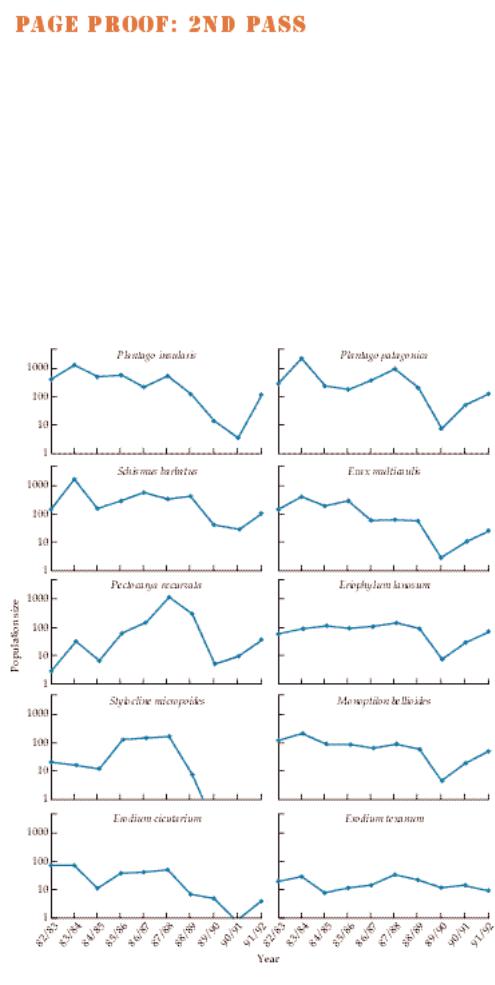
ronments, for example, have highly variable rainfall. In a 10-year study of winter annuals in the Sonoran Desert, Lawrence Venable and Catherine Pake (Venable and Pake 1999) documented major variation from year to year in the realized fecundity (the chance of surviving to maturity times the fecundity of survivors) of ten species of these plants (Figure 7.14). This variation underlies fluctuations in the population sizes of these species (Figure 7.15). Interestingly, years in which realized fecundity is high appear to be associated with El Niño events (Venable and Pake 1999; see Chapter 18).
Second, in the case of demographic stochasticity, the chance variation in the fates of individuals reduces the average long-term growth rate of the population. Con-
Population Structure, Growth, and Decline 137
sider a population of eight plants with a probability P = 0.25 of an individual surviving until next year. There is a fair chance that next year’s population will not be two, the product of P and n (this year’s population). (For further insight, see the discussion of genetic drift in Chapter 5, with which demographic stochasticity shares many properties.)
Some important features of demographic stochasticity are shown in Figure 7.16. Figure 7.16A shows the observed number of survivors in a hypothetical population in which individuals have a probability of 0.25 of surviving. You might notice that there are more extremely low values than extremely high values. There is a reason for this: Even in a population of 1000 plants,
Figure 7.15
Fluctuations in population size in ten species of Sonoran Desert winter annuals. (After Venable and Pake 1999.)

138 Chapter 7
Figure 7.16
The effect of demographic stochasticity on survival in a hypothetical population with a survival probability of 0.25.
(A) The observed number of survivors given a population size of N where survivorship rates were determined by the average survival probability plus a deviation due to random chance. The line shows the expected number of survivors: 0.25 times the population size. (B) The relative size of the departure from the expected value: (number of survivors – expected survivors)/expected survivors.
it is possible that, by chance, no plants will survive—but it is never possible for more than 1000 to survive. Figure 7.16B shows the relative departure from the expected number of survivors, which tends to be greater in small populations.
Both forms of stochasticity occur in all populations. Environmental stochasticity can have substantial effects in populations of any size. As the examples above suggest, demographic stochasticity is important mainly in small populations.
Long-Term Growth Rates
Imagine a population of annual plants (without a seed bank) that grows, in good years, at the rate λg = 1.01, and in bad years, at the rate λb = 0.99. To keep things simple, imagine that good and bad years alternate. It may surprise you to realize that this population is slowly going extinct! How can this be, when the average rate of growth is obviously 1? It is because the long-term growth rate is not an ordinary arithmetic average, but is equal to the square root of 1.01 × 0.99, which is less than 1. Why? Population growth is a multiplicative process: seeds produced in good years then germinate in bad years, and vice versa. The square root thus gives us the appropriate average over time.
Given an average rate of population growth, variation in that rate among years reduces the long-term rate of population growth. Consider a group of unstructured populations—such as annual plants without seed banks—having the possible values of λ that are given in the second column of Table 7.4, and assume that these values occur with equal probability. The average value of λ is the same for populations 1–3, but λ varies more in population 3 than in population 2, and it does not vary at all in population 1. The average value of λ is called the arithmetic mean and is symbolized λ . The arithmetic mean of n numbers is their sum divided by n (see the Appendix).
Although populations 1–3 all have the same average growth rate, their long-term growth rates differ, because population growth is a multiplicative process. Next year population 1, whose growth rate does not vary, will be 1.03 times its current size, and in 8 years it will be 1.038 = 1.267 times its current size. If the two different values of λ occur for population 2 with equal probability, that population will grow at some different rate, such as 1.05 × 1.01 × 1.01 × 1.01 × 1.05 × 1.01 × 1.05 × 1.05. In this example, population 2 will be about 1.264 times its current size in 8 years—it will have grown less than population 1.
The long-term growth rate of an unstructured population is given by the geometric mean of the annual λ’s, symbolized as a in the fifth column of Table 7.4. (The geometric mean of n numbers is the nth root of their product.) The geometric mean has an important property: it is guaranteed never to exceed the arithmetic mean, and is equal to the arithmetic mean only if the n numbers are all the same—in other words, if the variance of λ is 0 (see the Appendix for a discussion of variance). For a given average growth rate λ , then, increasing the variance of λ always reduces the long-term growth of the population.
This discussion might be interpreted to mean that increasing the variance of λ always reduces a, but this is true only if the average growth rate λ stays constant. Population 4 has a larger arithmetic mean and a larger

Population Structure, Growth, and Decline 139
Table 7.4 Relationship between annual and long-term population growth rates in a variable environment
|
Values |
Arithmetic |
Variance |
Geometric |
Population |
of λ |
mean (λ) |
(σ 2 ) |
mean a |
|
|
|
λ |
|
1 |
1.03 |
1.03 |
0 |
1.03 |
2 |
1.01, 1.05 |
1.03 |
0.0008 |
1.0298 |
3 |
1, 1.01, 1.05, 1.06 |
1.03 |
0.0009 |
1.0297 |
4 |
1, 1.01, 1.05, 1.07 |
1.0325 |
0.0011 |
1.0321 |
5 |
0.9, 1.01, 1.05, 1.17 |
1.0325 |
0.0124 |
1.0280 |
Note: The long-term growth rate depends on the mean and variance of yearly rates. In unstructured populations, the long-term rate is the geometric mean of the yearly rates.
variance in λ, and its long-term growth rate is larger than any of populations 1–3. On the other hand, population 5 has still greater variance in λ, and its long-term growth rate is the smallest of the five populations.
These examples should help to convince you that both the average conditions and their variation are important in determining long-term rates of population growth. There are few studies on this kind of long-term variation. There are many anecdotal accounts of plants in highly variable environments (such as desert annuals) that usually have high mortality and low fertility, but in an occasional “good year” produce vast quantities of seed. Thus it is possible for a plant population to have positive growth in the long run, but be declining in numbers during most years (Venable and Pake 1999).
These general ideas hold for ageand stage-struc- tured populations as well. To study population growth in a stochastic environment, we use the stochastic growth rate a rather than λ1. In structured populations, a is the long-term average growth rate of the population. Generally, a must be estimated by simulation. Because matrix multiplication is not commutative, a is not a simple geometric mean of the estimate annual growth rates (see Caswell 2001 for a discussion of methods for estimating a). Just as the geometric mean of a sequence of numbers is smaller than the arithmetic mean, a is less than λ1 unless there is no stochasticity, in which case the two quantities are equal. Calculations of the long-term growth rate are actually done with logarithms analogous to r = ln(λ).
Studying Variable Population Growth
To study the effects of environmental stochasticity, one needs the same kinds of data used to estimate average population growth rates, recorded over enough years to estimate the variances and covariances of the matrix elements—the survivorship and fecundity rates. Given such data, one can perform computer simulations of population growth that is subject to random variation. There are many studies reporting variation in matrix elements (e.g., Horvitz and Schemske 1990; Bierzychudek 1982).
Few of these studies, however, are of sufficient length to provide good estimates of variance, and fewer still provide estimates of the covariance among matrix elements.
Even a population with a > 1 can sometimes go extinct due to random variation. A population’s extinction probability is estimated as the fraction of replicate populations that can be expected to go extinct. This value is estimated by simulation. Extinction probabilities for several California species of Calochortus (mariposa lily, Liliaceae) are shown in Figure 7.17. Note that extinction probabilities increase as the amount of environmental stochasticity increases, and that this increase is fastest for populations with the smallest value of λ.
An idea that is very closely related to extinction probability is the minimum viable population (MVP). The MVP is the minimum size necessary to give a population a probability x of surviving t years. Typically the probability is taken as 0.95, and the time as 50 or 100 years. Plans for the management of endangered species increasingly require estimates of MVP. Eric Menges (1992) conducted simulations to estimate the MVP for the Mexican palm Astrocaryum mexicanum (chocho, Arecaceae), using published matrices from the extensive study of Piñero et al. (1984); the results are shown in Figure 7.18. Populations subject to only demographic stochasticity could begin with only 50 plants and still have a 95% chance of persisting 100 years. Populations subject to environmental stochasticity required larger initial sizes to have this chance of persisting. As environmental stochasticity became large (i.e., there was more year- to-year variation), the chance of a population going extinct increased rapidly in smaller populations.
Most demographic studies of plants have lasted only a few years, and consequently have focused on
average values of growth rates λ .These are useful quan-
tities, but it is important to realize that λ overestimates
a (just as the arithmetic mean is always larger than the geometric mean, unless the variance is zero). There have been few attempts to estimate a in plant populations. Hal Caswell (2001) estimated a for two populations of

140 Chapter 7
(A)
Figure 7.17
(A) Calochortus howellii (Mariposa lily, Liliaceae), which is endemic to southwestern Oregon, especially serpentine areas. (Photograph courtesy of J. Sainz.) (B) Extinction probabilities of several California populations of Calochortus spp. Environmental stochasticity was modeled by taking 1% of the variance/
mean for seed production, and 0.01% of the variance/mean for other vital rates, and then multiplying these values by the numbers shown on the horizontal axis. (After Menges 1992.)
Figure 7.18
Results of a simulation conducted to estimate the minimum viable population (MVP) size for a population of the Mexican palm Astrocaryum mexicanum (chocho, Arecaceae) under different levels of environmental stochasticity (ES). Environmental stochasticity was modeled using the methods described in Figure 7.16. MVP is the smallest number giving an extinction probability of 5% or less in 100 years. (After Menges 1992.)

Arisaema triphyllum (jack-in-the-pulpit, Araceae) in New York state studied by Paulette Bierzychudek (1982). In this study, a and its 95% confidence intervals were 1.2926
± 0.0025 in the Fall Creek population, and 0.8979 ± 0.0028 in the Brooktondale population.
Summary
Studies of change in plant populations require defining an “individual.” In many plants, unlike most animals, genetic and physiological individuals are different because many genetic individuals can reproduce vegetatively as well as sexually. The “right” kind of individual to study depends on the questions being asked.
Survival and reproductive rates in plants usually depend much more on stages (size, life history stage, physiological status) than on ages. An important goal of plant population studies is identifying the factors causing variation in survival and reproductive rates. Most population models use stages to study changes in population size.
Additional Readings
Classic References
Harper, J. L. 1977. Population Ecology of Plants. Academic Press, London.
Hartshorn, G. S. 1975. A matrix model of tree population dynamics. In Tropical Ecological Systems, F. B. Golley and E. Medin (eds.), pp. 41–51. Springer-Verlag, New York.
Contemporary Research
Horvitz, C. C. and D. W. Schemske. 1990. Spatiotemporal variation in demographic transitions for a tropical understory herb: Projection matrix analysis. Ecol. Monogr. 65: 155–192.
Platt, W. J. and S. L. Rathbun. 1993. Dynamics of an old-growth longleaf pine population. In The Longleaf Pine Ecosystem: Ecology, Restoration and Management, S. M. Hermann (ed.), pp. 275–297. Proceedings of the Tall Timbers Fire Ecology Conference, No. 18.
Population Structure, Growth, and Decline 141
Matrix models are useful tools for studying change in population size and composition. They make it possible to estimate the population’s eventual growth rate and composition—an important way of examining the consequences of current demographic conditions. Reproductive value, which can be calculated from a transition matrix, is useful in comparing the importance of different stage classes for future population growth. It is now possible to calculate age-based quantities (such as the average age of first reproduction) from stage-based data.
Plant populations vary in their growth rates. One cause of this variation is random variation in the environment, which affects all plant populations. Variation in population growth rates is also caused by random events involving individuals. This kind of random variation is most important in small populations. Generalizations of matrix modeling approaches make it possible to estimate long-term population growth rates, extinction probabilities, and minimum viable population size.
Kalisz, S. and M. A. McPeek. 1992. Demography of an age-structured annual: Resampled projection matrices, elasticity analyses, and seed bank effects. Ecology 73: 1082–1093.
Additional Resources
Caswell, H. 2001. Matrix Population Models. 2nd ed. Sinauer Associates, Sunderland, MA.
Cochran, M. E. and S. Ellner. 1992. Simple methods for calculating age-based life history parameters for stage-structured populations. Ecol. Monogr. 62: 345–364.
Easterling, M. R., S. P. Ellner and P. M. Dixon. 2000. Size-specific sensitivity: Applying a new structured population model. Ecology 81: 694–708.
