Задание 15 |
Какие из следующих утверждений верны? |
|
|
(№ 169933) |
|
Если катет и гипотенуза прямоугольного 1 треугольника равны соответственно 
то второй катет этого треугольника
2Любые два равнобедренных треугольника о! подобны. Неверн
3Любые два прямоугольных треугольника о! подобны. Неверн
4Треугольник ABC, у которого АВ=3, является тупоугольным.
|
|
|
|
|
! |
|
|
|
|
о |
|
|
|
|
н |
|
|
|
|
р |
|
|
|
|
е |
|
|
|
|
ев |
|
|
|
|
|
Н |
|
|
|
|
|
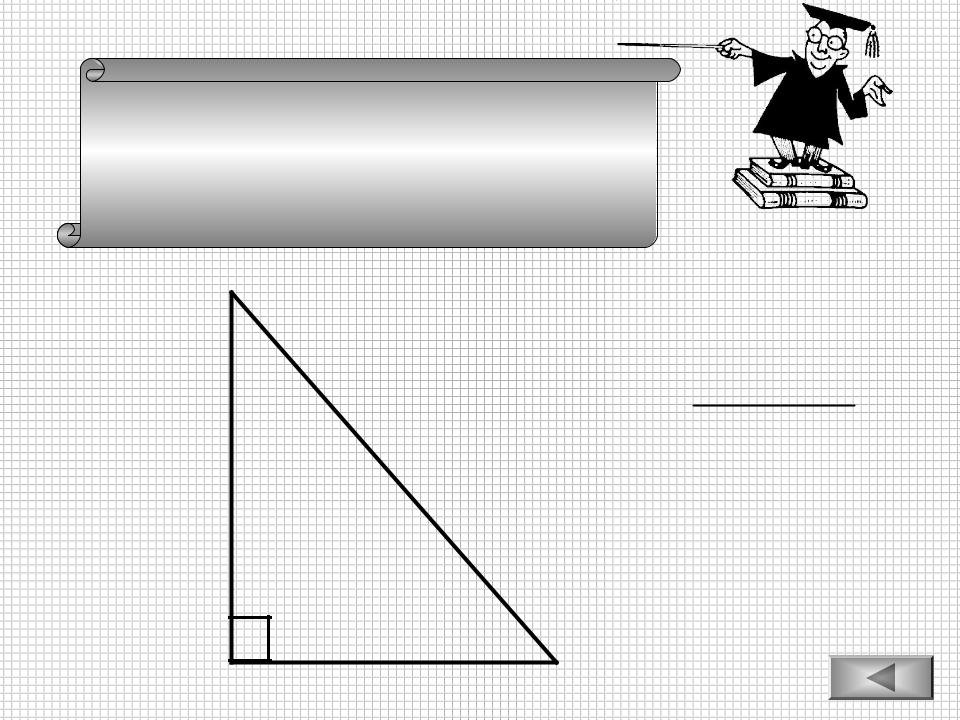
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
А
К а т е т
С
b
Г |
|
и |
|
п |
|
о |
|
|
т |
|
е |
c |
н |
з |
|
|
у |
|
а |
a
К а т е т
c2 a2 b2 a 
с2 b2
В
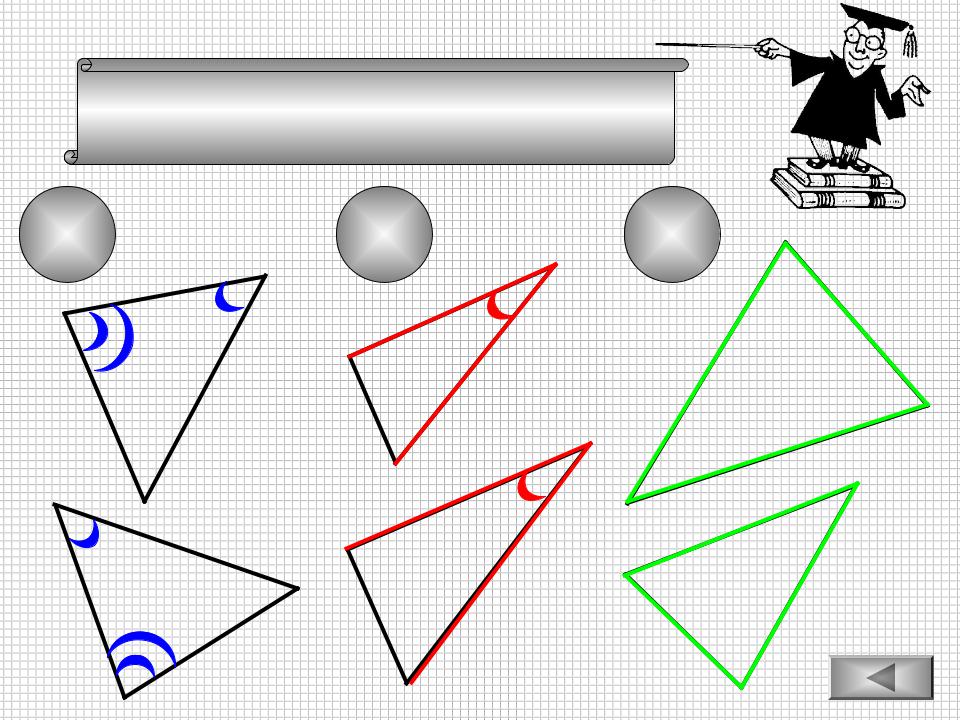
Вспомним признаки подобия треугольников
1 |
2 |
3 |
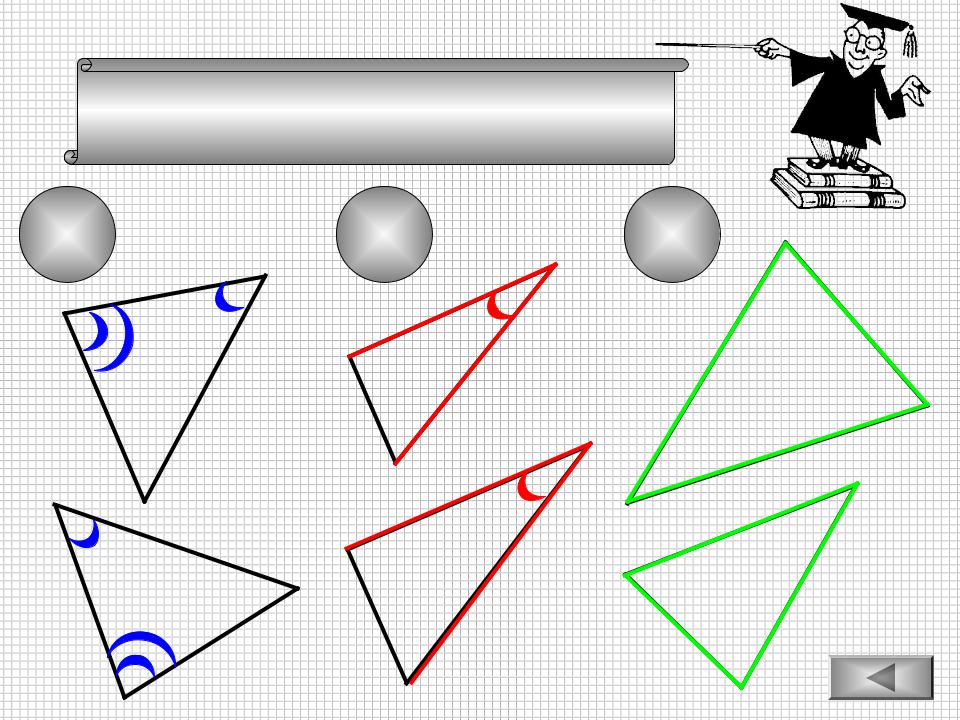
Вспомним признаки подобия треугольников
1 |
2 |
3 |
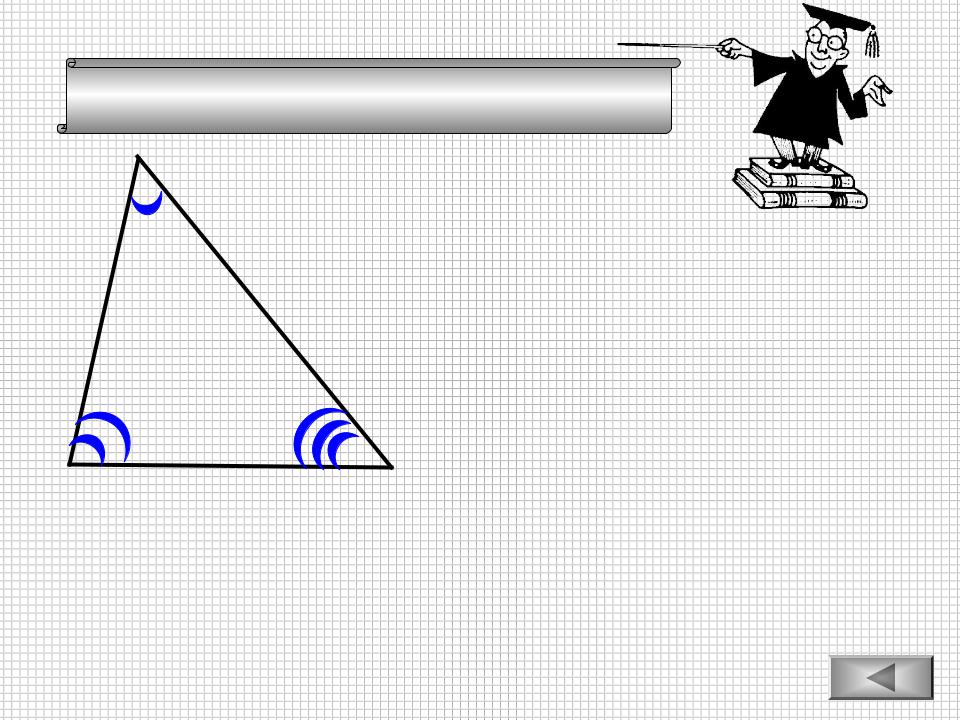
Теорема косинусов
А
c b
В |
a |
|
cos 0 |
cos 0 cos 0
c2 a2 b2 a2 c2 b2 b2 a2 c2
2abcos C
2cbcos A
2ac cos B
С
-угол острый
-угол прямой
-угол тупой
Задание 15 |
Какие из следующих утверждений верны? |
|
|
(№ 169935) |
|
1
Квадрат любой стороны тр-ка равен сумме
квадратов двух других сторон без |
|
|
|
! |
|
|
рно |
||
|
|
е |
|
|
|
ев |
|
|
|
произвед-ия этих сторон на sin угла |
Н |
|
|
|
|
|
|
|
|
2Если катеты прямоугольного треугольника . равны 5 и 12, то его гипотенуза равна Верно
3Треугольник ABC, у которого АВ=5, является остроугольным.
|
|
|
|
. |
|
|
|
о |
|
|
|
н |
|
|
|
р |
|
|
|
е |
|
|
|
|
В |
|
|
|
|
В прямоугольном треугольнике
4квадрат катета равен разности квадратов рно. гипотенузы и другого катета. Ве
Теорема косинусов
А
|
b |
c2 |
a2 |
|
c |
a |
2 c2 |
||
|
b2 a2
b2 2abcos C
b2 2cbcos A
c2 2ac cos B
В a
С
Теорема синусов
a |
|
b |
|
c |
|
|
|
||
sin A |
sin B |
sin C |
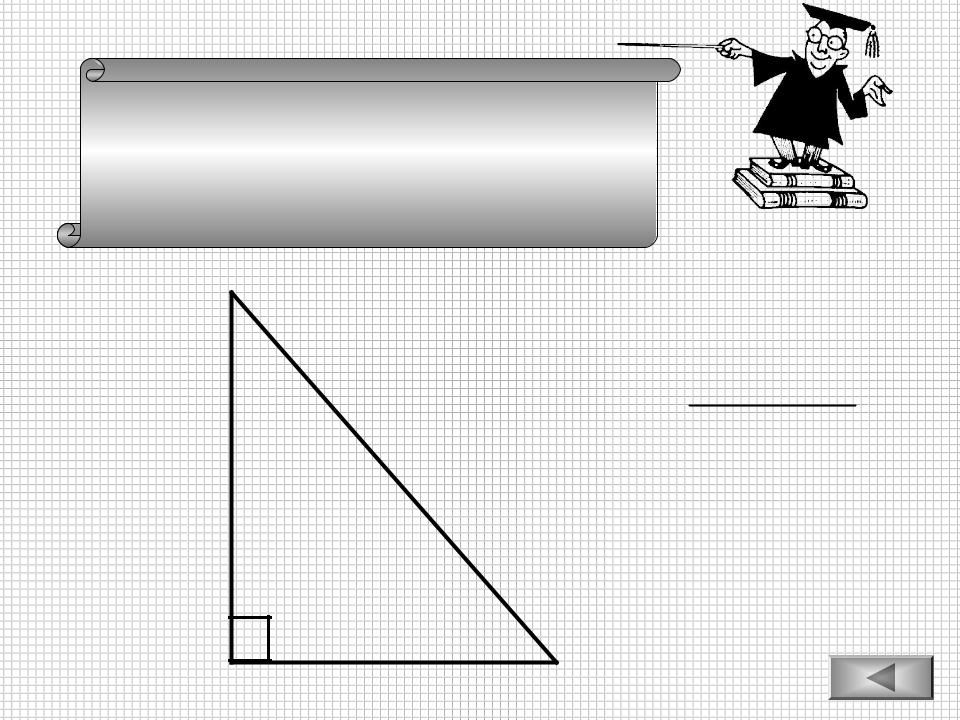
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
К а т е т
С
b
Г |
|
и |
|
п |
|
о |
|
|
т |
|
е |
c |
н |
з |
|
|
у |
|
а |
a
К а т е т
c2 a2 b2 с 
a2 b2
В
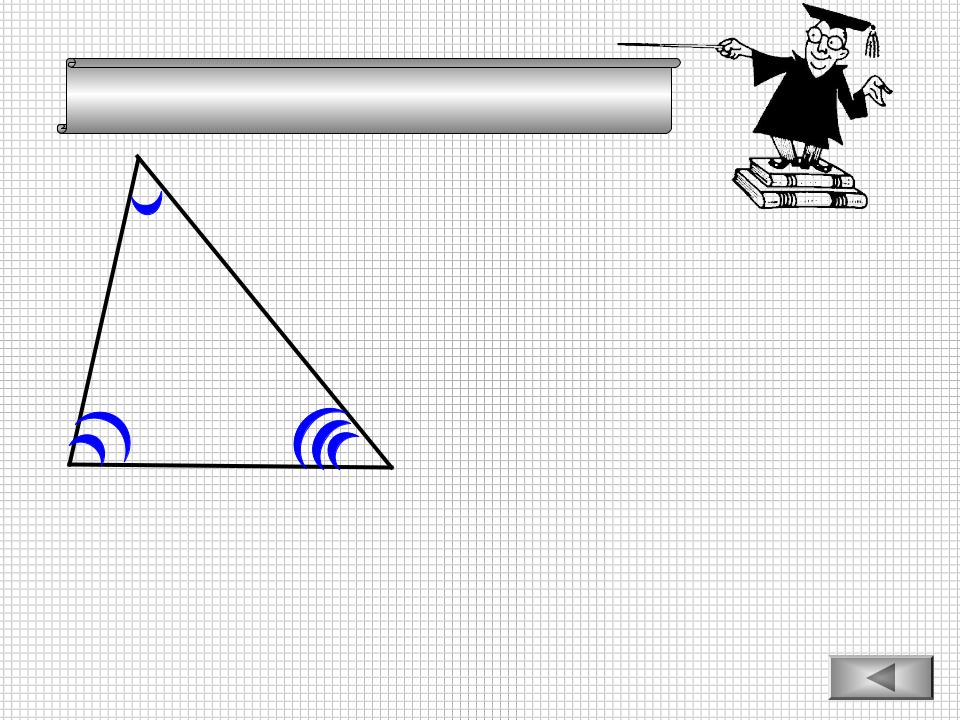
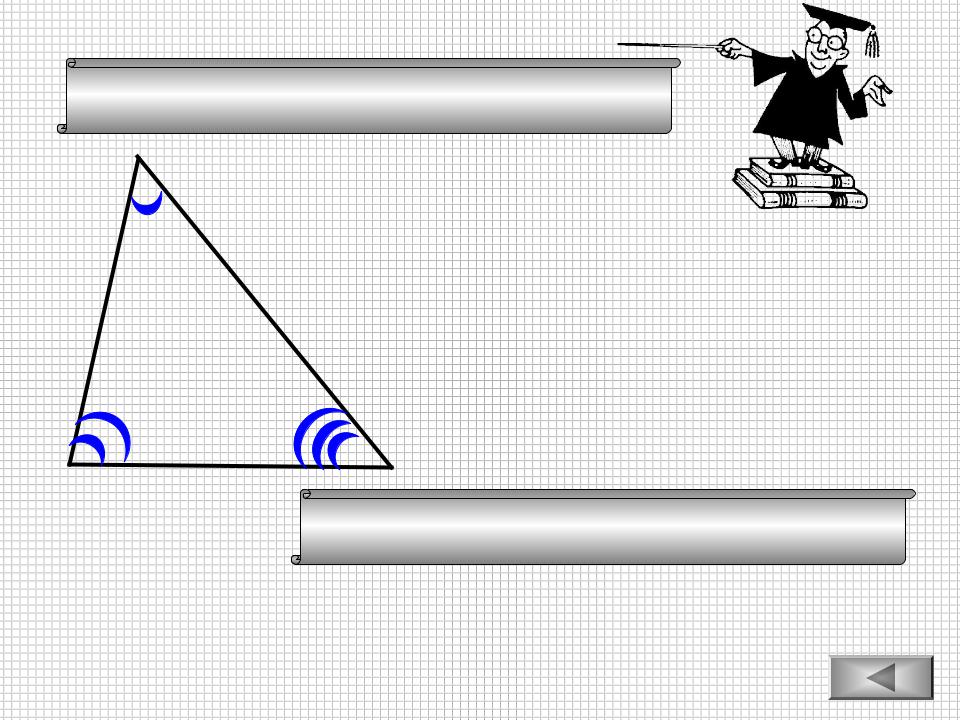
Теорема косинусов
А
c b
В |
a |
|
cos 0 |
cos 0 cos 0
c2 a2 b2 a2 c2 b2 b2 a2 c2
2abcos C
2cbcos A
2ac cos B
С
-угол острый
-угол прямой
-угол тупой
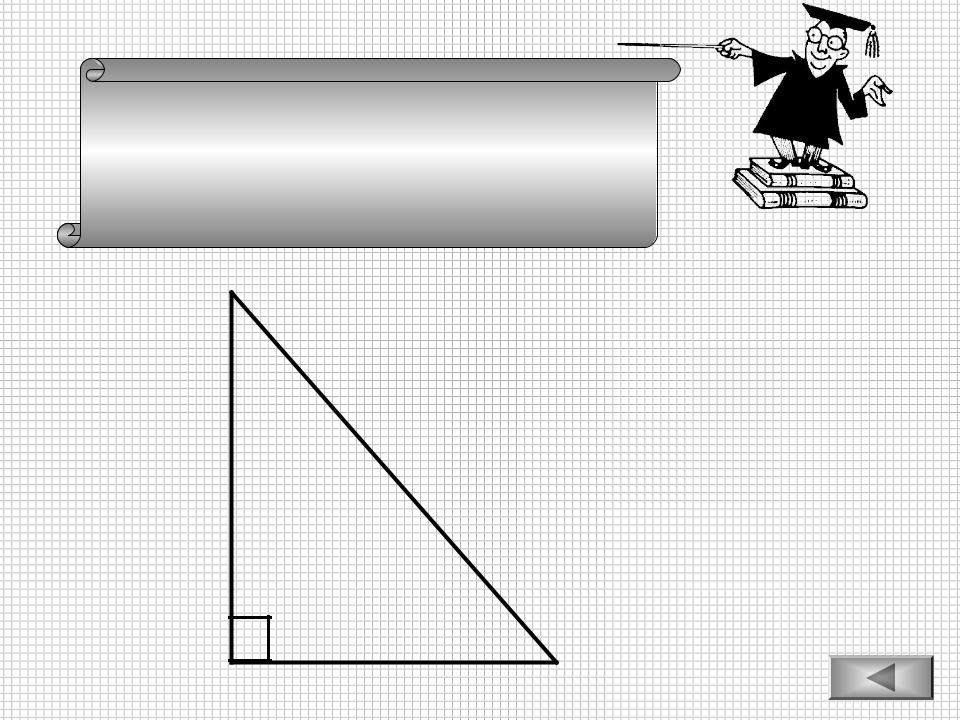
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
А
К а т е т
С
b
Г |
|
и |
|
п |
|
о |
|
|
т |
|
е |
c |
н |
з |
|
|
у |
|
а |
a
К а т е т
c2 a2 b2 a2 c2 b2
В