Вертикальными углами называются углы, стороны которых являются продолжением друг друга. Вертикальные углы равны.
Сумма углов четырехугольника равна 360°
33 |
|
Е В23 |
А |
?D |
41 С |
Повторение |
(2) |
ЕАD= DАС по условию, АЕ=АС по условию, АD - общая
∆ЕАD=∆DАС АЕD= АСD=41
ЕАD – внешний для ∆DВЕВDЕ=41 -23 =18
Ответ: 18.
34
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
35 |
D |
|
|
Найдите ВDЕ. |
? |
В |
|
Повторение |
Е |
104 |
|
(3) |
С |
10 |
А |
СВD и АВС СВD=180 -
ЕСВ – внешний для104∆АВС=76 ЕСВ=104 +10 =114
DСВ =½ЕСВ=57
По сумме углов тр-ка СDВ =180 -76 -57 =47 ∆СDЕ=∆СDВ ЕDВ =2 СDВ=2∙47 =94
Ответ: 94.
36
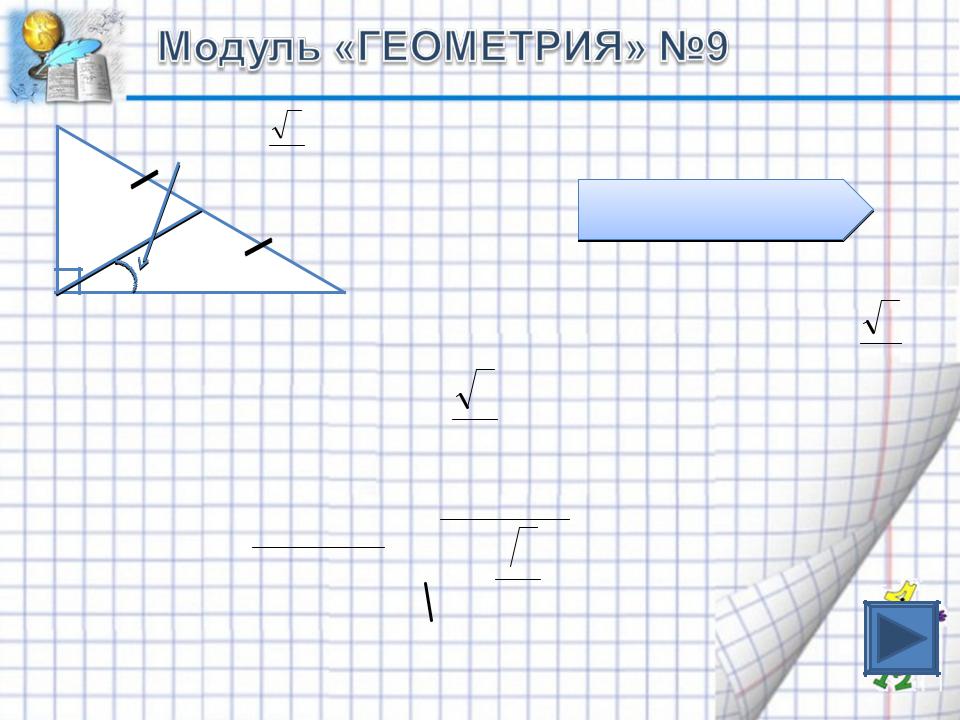
Если в треугольниках две стороны и угол между ними равны, то треугольники равны
В равных треугольниках соответственные углы равны
Если угол разбит на части, то его градусная мера равна сумме градусных мер его частей
37 |
В |
sin A=0,8. |
С
А
Найдите sin B.
Повторение |
(2) |
sin À cos  0,8 sin2 cos2 1
sin  
1 cos2 B 
1 0,82 0,6
Ответ: 0,6.
38
В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла
Основное тригонометрическое
2тождество:2
sin cos 1
39 |
В |
sin ÀÑÌ |
3 |
Найдите sin B. |
|
|
|
М |
2 |
|
Повторение |
|
С |
|
|
А |
(4) |
|
|
|
А+ В=90° |
|
||
|
|
|
|
3 |
|
Так как С= А+ В, то А= АСМ sin ÀÑÌ sin À |
|||||
|
|
|
|
3 |
2 |
|
sin À cos  |
|
|||
|
|
|
|
2 |
|
sin2 cos2 1
sin  
1 cos2 B 
1 (
23)2 12 0,5
Ответ: 0,5.
40 |
В прямоугольном треугольнике сумма острых углов равна 90
В равнобедренном треугольнике углы при основании равны
В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла
Основное тригонометрическое
тождество:
sin2 cos2 1
41 |