5.1.3. Цели и результаты обучения решению задач и использования задач в обучении младших школьников

Цели и результаты использования задач как средства обучения — это цели и результаты изучения тех понятий и способов действий, которые формируются с помощью задач. Они представлены в со­ответствующих главах. Цели и результаты использования задач как средства развития, воспитания, контроля реализуются одновременно с реализацией роли задач как средства обучения и как цели обучения. Поэтому остановимся на цели и результатах использования задач как цели обучения, т.е. цели формирования умения решать задачи.

Эффективно обучать сложному действию, каким является уме­ние решать задачи, можно в случае, если определены и описаны его компоненты так, что можно выстроить конструктивные программы обучения. Исследование этой проблемы позволило выделить два вида умения решать задачи: 1) общее умение решать задачи и 2) умение решать задачи определенного вида, а также конструктивных ком­понентов данных умений. (Ранее использовались термины «общие подходы к решению задач», «общие приемы решения»)

Общее умение решать задачи. Умение проявляется при решении задачи, способ решения которой решающему неизвестен. По харак­теру поведения при встрече с такой задачей решающих можно раз­делить на две группы. Решающие первой группы, обнаружив, что способ решения им неизвестен, никаких действий не совершают на том основании, что «мы такие задачи не решали и потому решить эту задачу я не смогу». Общее умение решать задачи у них заблоки­ровано общей установкой, поэтому не проявляется. При этом они

200

могут владеть некоторыми его компонентами и умением решать за­дачи определенных видов.

Решающие второй группы в той же ситуации начинают анализи­ровать, преобразовывать задачу, применяя общие приемы, доводят решение до выполнения требования или до обоснования отсутствия решения (что тоже является решением), либо после выполнения не­которой его части делают вывод о причинах неуспеха в решении, например: «Я не могу решить эту задачу, так как не знаю, что такое … …так как для решения нужно …, а я не умею это делать». Такие решающие владеют общим умением решать задачи.

Как уже отмечалось: «цель нельзя достичь, не имея критериев ее  достижения»¹, поэтому важным понятием методики обучения реше­нию задач являются понятия «критерии»² (признаки, показатели) сформированности у учащихся умения решать задачи, содержа­ние» и способы выявления уровня умений решать задачи». Такие критерии зададим для каждого вида умения решать задачи.

Критериями уровня общего умения решать задачи будем счи­тать адекватность задаче характера действий решающего и ис­пользуемых в процессе решения метода(ов), способа(ов) решения и уровень сложности успешно решенных задач.

Механизм общего умения решать задачи состоит в том, что ре­шающий при ознакомлении с задачей обнаруживает отсутствие в его памяти информации об опыте, методах, приемах и средствах реше­ния этой и подобных ей задач и потому применяет наиболее общие инструменты, помогающие восприятию и осмыслению содержания задачи, вычленению в исходной задаче серии подзадач. Эта работа проводится до вычленения подзадач, которые идентифицируются как задачи известных видов. Далее включается механизм работы умения решать задачи определенных видов.

Выделим показатели, по которым можно судить об уровне общего умения решать задачи:

а) отношение к процессу решения и задаче, способ решения ко­ торой неизвестен;

б) владение общими приемами, помогающими решению задач, методами, способами решения; адекватность их выбора конкретной задаче и собственным особенностям и возможностям;

в) уровень сложности и трудности незнакомых задач, которые правильно решает диагностируемый.

По показателю а) определяется понимание процесса решения задачи. Если он понимается как выполнение некоторой последова-

¹ Витяев Е. Е. Извлечение знаний из данных. Компьютерное познание. Мо­ дели когнитивных процессов: Монография. — Новосибирск, 2006. — С. 20.

² «Критерий … Признак, на основании которого производится оценка, опре­ деление или классификация чего-л.» (Ефремова Т. Ф. Современный толковый словарь русского языка: В 3 т. — Т. 1. — М., 2006.).

201

тельности арифметических действий по данному учителем образцу, то это препятствует овладению общим умением решать задачи. На­личие у учащегося убеждения в том, что решать можно только зада­чи, способ решения которых кем-то показан, которые уже решали с учителем, полностью блокирует становление общего умения. Это убеждение формируется только в процессе неправильного обучения. Проявлением этого убеждения является отказ учащегося от решения незнакомой задачи только на том основании, что «мы такие задачи не решали»¹.

По показателю б) определяется, какие приемы, методы и спосо­бы решения известны учащимся, что они знают о них, какие из них умеют успешно применять самостоятельно, какие могут применять с небольшой помощью учителя (зона ближайшего развития).

Для определения значения показателя в) необходимо охаракте­ризовать понятия сложность задачи и трудность задачи. Под слож­ностью задачи понимается объективная характеристика задачи, зависящая от количества и характера связей между элемента­ми содержания задачи, количества и характера определяемых ими операций, необходимых для решения. В решении может быть задействована бо#льшая или меньшая часть этих связей в зависи­мости от метода и способа решения. В информатике «сложностью задачи называют выраженную в виде функции от размерности вход­ных данных верхнюю границу числа операций, необходимых для вы­полнения этой задачи. Если задача формализована, то ее сложность можно определить как сложность наилучшего известного алгоритма для ее решения»².

Трудность задачи — это субъективная характеристика, зави­сящая от уровня подготовленности решающего к решению задач такого уровня сложности, как данная. Одна и та же задача для одного учащегося может быть очень трудной и потому не решаемой им, а для другого — легкой. Требования ФГОС НОО и Примерной основной образовательной программы задают базовый уровень слож­ности задач, умение решать которые входит в планируемые, требуе­мые результаты. Повышенный и высокий уровень в реальном обра-

¹В одном исследовании каждому учащемуся первого класса в индивидуальном порядке была предложена задача. В ней легко выделялись три подзадачи, реше­нию которых дети были хорошо обучены. После прочтения задачи все учащиеся говорили, что не смогут ее решить. Некоторые обосновали свой вывод так: «эта задача в три действия, а мы в три действия не решали». И когда экспериментатор просил назвать действия, то дети их называли и с помощью экспериментатора с удивлением узнавали, что задачу они решили.

² Воронов В. И. Информационные технологии в коммерческой деятельности / В.И.Воронов, В.А.Лазарев; ред. Л.В.Моисеева // Сайт цифровых учебно-ме­тодических материалов ВГУЭС [abc.vvsu.ru. http://abc.vvsu.ru/Books/u_Inf_teh/ page0025.asp] Дата обращения 03.09.2012.

202

зовательном процессе определяются Образовательной программой образовательного учреждения, педагогическим мастерством учителя и математическими способностями учащихся.

Приведем примеры заданий для выявления уровня общего уме­ния решать задачи.

Задания. •·1. Среди данных задач, выбери те, способы решения которых тебе неизвестны. Обрати внимание на задачи со «звездоч­ками», это задачи с «хитринками», «ловушками». Попробуй решить выбранные задачи. • 2. Вспомни методы решения задач, которые ты знаешь (арифметический, геометрический, с помощью уравне­ний, …). Для каждого метода выбери задачу, которую ты сможешь решить этим методом, реши ее. • 3. Реши данную задачу разными арифметическими (алгебраическими, геометрическими, практиче­скими, …) способами. • 4. Переформулируй данную задачу и запиши ее кратко. • 5. Построй геометрическую (табличную, предметную) модель данной задачи. • 6. Ознакомься с данными задачами. Опре­дели самую трудную, которую ты можешь решить. Для этого решай их в порядке возрастания трудности.

Умение решать задачи определенного вида. Умение проявляет­ся в узнавании задачи и применении к ней средств решения (методов, способов, приемов), наиболее адекватных этому виду (типу) задач.

Механизм умения решать задачи определенного вида таков. После узнавания задачи припоминается либо ситуация решения подобной задачи («Это такая же задача, как мы решали вчера, значит нужно как и там, вначале узнать сколько во второй коробке, а затем сколько в двух»), либо способ решения («Это задача на сравнение по вопро­су «на сколько больше». Такие задачи решаются вычитанием: нужно из большего числа вычесть меньшее»), либо подходящие средства решения («Это задача на движение. Решению таких задач помогает чертеж. Изобразим длину пути отрезком, скорость …»).

Показателями умения решать задачи определенного (заданного) вида назовем: а) знание признаков задач данного вида, проявляю­щееся при выборе задач этого вида из нескольких задач разных видов, схожих по сюжету (знание названия вида не учитывается); б) слож­ность правильно решенных выбранных задач данного вида.

Примеры заданий: «Выберите задачи, которые знаете как решать, и решите их», «Выберите задачи на движение и решите их». Если ре­шающий выполняет задание, значит, он владеет соответствующим умением. Его уровень и качество определяются степенью сходства выбираемых задач с образцами задач данного вида, уровнем слож­ности решенных задач, характером методов и способов решения.

Чтобы формировать умения решать задачи, нужно знать состав каждого умения. Определим его следующим образом.

Общее умение решать задачи состоит: из знаний о за­дачах, структуре задач, процессе решения, этапах решения (дей­ствиях по решению), методах, способах и приемах решения; уме-

203

ний применять названные знания в процессе решения конкретной задачи. Умение применять знания — это умения выполнять каждый из этапов решения любым из приемов его выполнения при решении любым из освоенных методов и способов решения, доводя этот про­цесс до выполнения требования задачи, доказательства невозможно­сти решения или до обнаружения, осознания препятствия, которое данному решающему не позволяет довести решение до выполнения требования.

Умение решать задачи определенных видов скла­дывается: из знания видов задач (знание называний вида не обяза­тельно), способов решения задач каждого вида; умений узнавать задачу данного вида среди других, выбирать соответствующие виду метод(ы), способ(ы), приемы решения и реализовать их при решении конкретной задачи этого вида.

В Примерной основной образовательной программе начально­го общего образования (2011. С. 103) подчеркнута направленность обучения решению задач на достижение метапредметных результа­тов, в частности «познавательных универсальных действий, в пер­вую очередь — логических и алгоритмических», а также действий «планирования последовательности шагов при решении задач; раз­личения способа и результата действия; выбора способа достижения поставленной цели; использования знаково-символических средств для моделирования математической ситуации, представления ин­формации; сравнения и классификации …. Особое значение имеет математика для формирования общего приема решения задач как универсального учебного действия…..» (выделено СГ.Царевой). Что такое «общий прием решения задач» не поясняется. Будем считать, что «формирование общего приема» это то же, что «формирование общего умения решать задачи».

Предметные результаты работы с задачами — умение решать задачи заданных уровней сложности и видов, в частности тексто­вые задачи, решаемые с помощью одного — двух арифметических действий. Важным предметным результатом будет также совершен­ствование умений решать другие виды математических задач: вы­числительные, геометрические, задачи на сравнение, преобразова­ние, измерение и т.д. Метапредметные результаты — овладение компонентами общего умения решать задачи, применимыми к ре­шению задач не только математических, но и из других учебных предметов.

Чтобы подготовиться к обучению решению задач и обучению с по­мощью задач, необходимо узнать содержание компонентов умений решать задачи, способы и формы организации обучения, учиться применять их. Этому посвящены следующие подразделы настоящей главы.

204

5.2. формирование умения решать задачи у учащихся начальной школы

5.2.1. формирование умения решать задачи: характеристика понятия

Решение задач это вид деятельности. Тогда формирование уме­ния решать задачи это формирование деятельности. Отнеся харак­теристику формирования учебной деятельности, данную В. В. Да­выдовым и А. К. Марковой, к деятельности решения задач и науче­ния решению задач, получим следующее понимание формирования умения решать задачи: формирование умения решать задачи есть «управление взрослым процессом становления этой деятельности, предполагающее отработку у школьника каждого компонента деятельности, их взаимосвязи, постепенную передачу отдельных компонентов этой деятельности самому ученику для самостоя­тельного осуществления без помощи учителя»¹.

Формирование общего умения решать задачи это: • формирова­ние знаний о задачах, процессе решения задачи, этапах (действиях) этого процесса, их назначении и содержании, приемах выполнения каждого этапа, методах и способах решения; • выработка умения при­менять указанные знания, методы и способы в решении задач.

При формировании общего умения решать задачи предметом изучения и овладения, содержанием обучения являются сведения о задачах (в широком понимании) и процессах решения задач, спо­собы действий по решению задач — приемы, помогающие выполне­нию каждого этапа и процесса решения в целом, методы и способы решения.

Формирование умения решать задачи определенного вида пред­полагает изучение и освоение сведений о возможных различиях задач, приводящих к различиям в способах решений; основных видах задач (на уровне узнавания); наиболее подходящих способах и методах их решения; приемах — общих способах действий, применение которых к задачам данного вида наиболее эффективно.

Указанное содержание может осваиваться в ходе специальных видов работы с задачей, в которых деятельность учащихся направ­лена на овладение умением решать задачи в целом и отдельными его компонентами в частности. Среди этих видов работы есть и должно быть и решение задач. Но решение не для получения «ответа», а для овладения способами, методами, приемами решения, приемами на­хождения разных способов решения задач и т. п. Такое решение никогда не заканчивается выполнением требования задачи. Одна-

¹ Давыдов В. В. Концепция учебной деятельности / В. В. Давыдов, А. К. Мар­кова // Вопросы психологии. — 1981. — № 6. — С. 19.

205

ко обучение решению задач, в особенности решению текстовых за­дач, зачастую отождествлялось и отождествляется с решением задач в процессе обучения.

5.2.2. обучение решению задач и решение задач в процессе обучения

Можно предположить, что причины отождествления названных понятий «решение задач» и «обучение решению задач» лежат в под­ходах к обучению математике, а также в особенностях самих тек­стовых задач. В первых массовых школах учили репродуктивными методами. Учитель показывал образец решения, учащиеся выучива­ли его и воспроизводили при решении подобных задач. При показе образца решения вычислительных, измерительных и других чисто математических задач через образец задавался алгоритм вычисления или измерения, т. е. общий способ решения. Выучивание решений таких задач постепенно было заменено выучиванием алгоритмов — общих способов.

С образцами решений текстовых задач такой переход на общий способ не случился, так как в целом процесс решения текстовой за­дачи — процесс не алгоритмический. Основная часть решения тек­стовой задачи — процесс построения математической модели задачи и этот процесс не алгоритмический ввиду многообразия сюжетов и текстов и многозначности слов естественного языка. Выделение типов текстовых задач и способов их решений не спасло положе­ние. Оставалось только решать, решать и решать. Однако решение задачи и обучение решению задачи — существенно разные виды деятельности.

Решение задачи — деятельность, направленная на задачу как на свой предмет; ее цель достигнута, когда выполнено требование. Обучение решению задач — взаимодействие учителя и учащихся, направленное на учащихся: они учатся решать, а учитель помогает им в этом.

В табл. 5.1 показаны различия деятельности учащихся при реше­нии задачи в процессе обучения и при обучении решению задач, в котором учащийся выполняет учебную деятельность.

Таблица 5.1

	Деятельность учащегося
Критерии оценки	Решение задачи	Овладение умением решать задачи
Субъект	Учащийся	Учащийся
Предмет	Задача	Учащийся

206

Продолжение табл. 5.1

	Деятельность учащегося
Критерии оценки	Решение задачи	Овладение умением решать задачи
Цель	Выполнить требова­ние задачи: найти значение величины, объект, число, отно­шение, обосновать истинность утвержде­ния, построить объ­ект и т.д. — цель внешняя	Изменить себя: овладеть знаниями о задачах и процессе решения за­дач, способами действий, обеспечивающими воз­можность успешно ре­шать задачи новых видов и (или) более высокого уровня сложности, чем решаемые им до выпол­нения данной деятельно­сти, усовершенствовать, увеличить степень владе­ния уже присвоенными способами действий — цель внутренняя
Действия	Восприятие и осмыс­ление задачи, поиск и составление плана решения, выполнение плана, проверка. Или подбор и угадывание ответа, присвоение чужого ответа и реше­ния	Наблюдение за собствен­ным решением задачи, рефлексия при решении и выполнении иных дей­ствий с задачами: сверну­том, интуитивном, логиче­ски развернутом решении, решении методом проб и ошибок, с применением разных методов, приемов, способов, средств; само­стоятельное и групповое; работа с информацией о задачах, процессах реше­ния задач; выполнение ча­сти решения, сравнение, преобразование задач и решений и т.д.
Условия прекра­щения действий	Получение ответа на вопрос задачи, по­строение требуемого объекта, вывода, от­ношения	Не существует, так как нет предела совершен­ствованию умения решать задачи. Прекращение де­ятельности может проис-

207

Окончание табл. 5.1

	Деятельность учащегося
Критерии оценки	Решение задачи	Овладение умением решать задачи
		ходить по причине: исте­чения времени, выделен­ного на эту деятельность; усталости; потери интере­са, в частности вслед­ствие переживаемого неу­спеха; внешних обстоя­тельств; признания доста­точности имеющегося уровня умения решать за­дачи
Результат	Заявленный в требо­вании задачи объект	Внутренние новообразо­вания: владение новыми способами действий, но­выми умениями, интел­лектуальное и эмоцио­нальное развитие и др.
Предмет контроля	Решение задачи, от­вет	Внутреннее состояние субъекта, уровень умения решать задачи
Предмет оценки	Качества решения	Уровень и качество уме­ния обучающегося — вну­тренние качества субъек­та
Возможность, при­знаки достижения цели. Сохранение результата	Выполненное требо­вание, устно (пись­менно) изложенный способ решения. Ре­зультат сохраняется	Полное и абсолютное до­стижение цели «научить­ся решать задачи» невоз­можно: нет предела со­вершенствованию и раз­витию умения решать за­дачи. Возможно достижение цели на неко­тором уровне. Сохране­ние умения и его совер­шенствование возможны только в специальной де­ятельности, включающей решение задач

208

5.2.3. формирование представлений о задачах и процессе решения задач

Основные понятия, представляющие задачи и деятельность че­ловека, направленную на выполнение требования задачи — это по­нятия задача, процесс решения задачи и решение задачи, решить и решать задачу, методы, способы и формы решения задач, при­емы выполнения этапов решения (приемы, помогающие решению) любых задач и задач определенных видов. Раскрыть их содержа­ние, значит ответить на вопросы: • Что такое задача? • Что зна­чит решить задачу; решать задачу? Что такое решение задачи?

• Из чего может состоять процесс решения задачи? • Какие суще­ ствуют приемы, способы, методы, формы решения задач? • Когда задача может считаться решенной? (Будем говорить о любых за­ дачах, уделяя основное внимание в примерах и в некоторых других случаях текстовым задачам.)

Задача. Это широкое общенаучное понятие. Слово «задача» в рус­ском языке имеет несколько значений и используется в речи в повсед­невном и профессиональном общении, при обучении всем учебным предметам. Дети задолго до школы слышат это слово в речи взрослых, встречают его в сказках, в произведениях других жанров, которые им читают взрослые, оно может быть в лексике дошкольника.

Понятию задача ввиду его широты нельзя дать строгое опреде­ление, поэтому его характеризуют через выделение общих и отличи­тельных признаков соответствующих объектов. Сделаем это и мы.

Вспомните несколько задач, которые вы когда-либо решали.

Педагогическая ситуация (С. Е. Царева). Первоклассникам задан во­прос: «Как вы думаете, взрослые решают задачи?» и дети дружно и по­чему-то радостно «выдохнули»: «Нет». В беседе выяснилось: они убежде­ны, что задачи есть только в школе и только на уроках математики. Что­бы изменить это мнение, говорю о задачах, которые только что решала: «На дворе ясно. По прогнозам — возможен дождь. Брать или не брать зонт?»; «От моей остановки до школы я могу доехать на маршрутном так­си за 10 — 15 мин. На путь до остановки из дома и от остановки до школы, на подготовку к уроку мне нужно еще 30 мин. За сколько минут до начала урока мне нужно выйти из дома?». Потом и дети привели примеры задач, которые решают не только дети, и не только на уроках в школе.

Задачи. • 1. (Шуточная задача.) Представьте себе, что вы маши­нист электропоезда. Поезд идет 2 ч со скоростью 60 км/ч, делая пять остановок по 2 мин. Сколько лет машинисту? • 2. Вычисли: 329 : 4.

• 3. Построй квадрат со стороной 5 см. • 4. Реши уравнение 7 + х = 10.

• 5. (Педагогическая задача.) Идет урок, изучается прямой угол. Вдруг Костя говорит: «А я не согласен, что это прямой угол. Какой же он пря­мой, если у него вон какой изгиб? Прямой — это когда без изгибов!» Как реализовать развивающий потенциал этой реплики?»

209

Что общего во всех задачах? Чем они похожи? Что есть в каждой задаче? Это вопросы и для обсуждения с учащимися на уроках, где понятие задачи будет предметом изучения.

Любая задача, реально возникшая у человека, зафиксированная в тексте или представленная другим образом (наличной ситуацией, рисунком, таблицей и т.д.), содержит в себе некоторую информа­цию о какой-либо ситуации из некоторой области действитель­ности и требование получить новую информацию об определен­ных компонентах той же ситуации, либо построить на основе данной информации новый объект, способ действия, установить, подтвердить или опровергнуть истинность некоторого утверж­дения.

Одну часть задачи, в которой задана информация, принято на­зывать условием задачи, другую — в которой указывается, что тре­буется найти, узнать, построить, сделать, доказать — требованием задачи.

Условие задачи содержит информацию о том, о чем спрашива­ется в требовании задачи — данные, может содержать неизвестные. Информация может быть представлена явно и (или) неявно. Текст: «Покупатель приобрел два пирожных по 20 руб. каждое. Какова площадь магазина?» не является задачей, так как заданная в тексте информация не связана с тем, что требуется узнать. Соотнесенность условия и требования задачи не всегда очевидна. Текстовые задачи часто потому и трудны, что связь условия и требования непрямая, скрытая, сложная.

В требовании характеризуется искомое, требуемое. Требование задачи может быть выражено побудительным или вопросительным предложением, вопросом: «Найти площадь квадрата», «Чему равна площадь квадрата?»; «Найдите способы поиска бракованной детали», «Как найти бракованную деталь?»; «Найти кратчайший путь от шко­лы до дома», «Какой путь от школы до дома кратчайший?»

В тексте задачи условие и требование могут находиться в разных предложениях или в одном. Обычно требование завершает текст за­дачи. Однако оно может находиться и в начале, и в середине текста. Умения выделять условие и требование в каждой задаче — компо­нент общего умения решать задачи. Формирование этого умения — составная часть формирования общего умения решать задачи.

Основные виды заданий: 1) выдели в данном тексте задачи условие и требование. (Полезно предлагать тексты с разным расположением требования; тексты задач, которые дети могут решить, и которые им еще не по силам, задачи текстовые и вычислительные, уравнения и другие, задачи по другим учебным предметам.); 2) к данному усло­вию подбери (составь) требование; 3) к данному требованию подбе­ри (составь) условие; 4) преобразуй текст задачи, поместив условие и требование в одно предложение; разные предложения, условие впереди (после) требования.

210

(1) У Оли О О CJ, у Саши а Ш. Сколько грибов у Оли и Саши вместе?

ft ft

2. У Оли L_ — 3, у Саши L. — 2 . Сколько грибов у Оли и Саши вместе?

3. У Оли 3 гриба, у Саши — 2 гриба. Сколько грибов у Оли и Саши вместе?

4. У Оли 16 грибов, у Саши — 7 грибов. Сколько грибов у Оли и Саши вместе?

Рис. 5.1

Необходимо также различать понятие задачи, определяемое фор­мальными признаками, и задачи как психологического понятия, как задачи для воспринимающего субъекта. Текст, содержащий фор­мальные признаки задачи не всегда является задачей для конкретного человека. Например, текст «На тарелке 2 красных яблока и 1 зеле­ное. Сколько яблок на тарелке?» для большинства первоклассников и взрослых не является задачей, потому что еще до прочтения во­проса мы преобразуем 2 и 1 в 3, вопрос сразу же заменяется ответом на него: «На тарелке 3 яблока». Задача решена, снята, ее нет.

Задача в психологическом смысле¹ — это текст (или ситуация), содержащий информацию и соответствующее требование (вопрос), которое воспринимающий задачу субъект не может «сходу» выпол­нить, не знает ответ на вопрос. Если по ходу восприятия текста или ситуации субъект выполняет требование, «видит» ответ на вопрос, то такой текст или ситуация задачей для него не является.

Дети все воспринимают психологически. У них еще нет опыта фор­мальных договоренностей. Если задача представлена так, что ответ на вопрос виден ребенку, то задачи для него нет. Особенно важно учи­тывать это при первом разговоре с детьми о том, что такое задача.

На рис. 5.1 одна и та же задача (в последнем варианте изменены только числовые данные) представлена в четырех видах.

Текст (1) для старших дошкольников и первоклассников задачей не является. Они видят все грибы и легко отвечают на вопрос, пока­зывая все грибы, а большинство могут дать и полный ответ: «У Оли и Саши вместе пять грибов».

Если первый разговор о задачах провести на примере текста (1), то нам не удастся обеспечить понимание смысла этого понятия. Ведь ответ на вопрос задачи дети видят, едва взглянув на рисунок. Для них — вижу, значит — знаю. Задачная ситуация исчерпана, задачи нет! А учитель говорит, что общее число грибов неизвестно, что это вопрос задачи, на который нужно искать ответ, что задачу нужно решать?!

Поставьте себя на место первоклассника. Он много раз отвечал на вопросы «Сколько у тебя игрушек (кукол, конфет и т. п.)?», пока­зывая предметы или называя их число. И все понимали и принимали.

Гурова Л. Л. Психологический анализ решения задач. — Воронеж. 1976.

211

А теперь обнаруживается: то, что он видит и знает — это неизвестное, которое надо найти, а для этого нужно еще и что-то рисовать, писать. И только потом говорить то, что знал с самого начала. Что чувству­ет ребенок?! И что он поймет? Что решать задачу — это некоторый набор действий, который просто нужно запомнить и выполнять, он никакого отношения не имеет к ответу на вопрос?

Тексты (2)—(4) больше могут претендовать на роль задачи при первом обсуждении вопроса о том, что такое задача.

Текст (1) не являясь задачей в психологическом смысле, может быть полезен для эффективной работы по исследованию способов и форм передачи информации о количестве предметов («штук»). — Как нам сообщается в этом тексте, сколько грибов у Оли и Саши? (Рисунком.) — Только ли рисуя грибы, можно в рисунке сообщить об их количестве? (Нет, можно нарисовать такое же количество кру­жочков, палочек, черточек, поставить столько же точек, т.е. услов­ным рисунком.) — Можно ли отрезком показать количество грибов? (После обсуждения: да, для этого нужно провести отрезок, который состоит из стольких мерок (такой длины при измерении выбранны­ми мерками), сколько грибов.) — Можно ли устно кому-то сказать, сколько грибов? (Да. Нужно назвать число, числа: «У Оли три гриба, у Саши два гриба. Всего грибов пять.») — Как это записать? (Цифра­ми: 3, 2 и 5.) — Как в записи показать, что 3 и 2 гриба объединены, что 5 грибов — это 3 и 2 гриба вместе? (3 + 2 = 5). — Итак, сколько способов мы нашли для того, чтобы представить, передать инфор­мацию о количестве грибов? (Дети перечисляют способы.)

Иногда общее понятие «задача» наделяется свойствами только понятия «арифметическая задача» (задача, ответ на вопрос которой находится с помощью арифметических действий) без использования слова «арифметическая». Такая подмена затрудняет формирование умения решать задачи, снижает образовательный и развивающий потенциал и самих арифметических задач.

Еще одна ошибка в характеристике понятия задачи заключает­ся в том, что в число структурных компонентов задачи включают элементы процесса решения задачи, например, такие как решение, ответ и другие. Структурных компонентов задачи два: условие и требование (вопрос), в которых, в свою очередь, выделяют их элементы (рис. 5.2).

Задача

Условие Требование

_{/ \ I}

Данные Неизвестные Искомое, требуемое

Рис. 5.2

212

Задача

Математические Нематематические

«Чисто Прикладные Психологические Химические Физические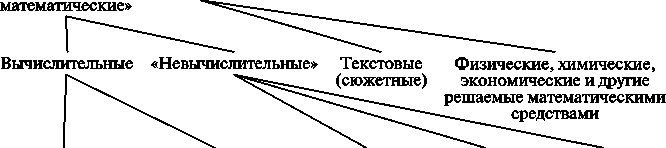

На выполнение На нахождение Преобразование Уравнения Геометрические одного действия значений выражений выражений и неравенства задачи в два и более действий

Рис. 5.3

Важный аспект понятия задачи — его вариативные свойства. Напомним: любое понятие тогда «работает» на образование, когда обу­чающиеся обсуждают не только общие свойства объединенных в нем объектов, но и вариативные, позволяющие различать представителей понятия — элементы объема понятия, образовывать новые, видовые понятия. Вариативные свойства понятия «задача» — это ответы на во­просы: «Чем может отличаться одна задача от другой?»; «Какие задачи возможны («бывают», существуют)?» Нужно, чтобы эти вопросы воз­никали у учащихся, чтобы было организовано их обсуждение.

Задачи могут отличаться друг от друга содержанием. По этому признаку выделяют группы задач: математические, лингвистические, психологические, кулинарные, педагогические, коммуникативные и др., а внутри каждой группы — подгруппы. Математические задачи подразделяют на две группы: прикладные и собственно математиче­ские. Текстовые задачи относятся к прикладным задачам (рис. 5.3).

В начальной школе дети обучаются умению решать математиче­ские задачи (вычислительные, геометрические, на преобразование математических выражений, на обоснование правильности утвержде­ний, уравнения и т. п.) и задачи прикладные математические — тек­стовые сюжетные задачи. Обучение решению задач первой группы происходит в связи с изучением соответствующих тем. Термин «за­дача» к такого рода задачам долгое время применялся только в основ­ной и старшей школе. Сегодня и в начальной школе оправдано и це­лесообразно использование термина «задача» ко всем видам задач.

Задачи могут отличаться характером требования. По этому при­знаку выделяют задачи на нахождение искомого, на построение, на конструирование (материального или идеального объекта, спо­соба действия и т.д.); на доказательство; на сравнение — на уста­новление сходства и различий, на определение вида отношения и др.

213

Существует классификация по предпочтительным методам и спосо­бам решения. В ней задачи делят на арифметические, алгебраические, геометрические, логические, практические; на нахождение четверто­го пропорционального, «на части», на «приведение к единице» и т.п. Возможны классификации и по многим другим основаниям.

Приобретение знаний о задачах учащимися начальной школы наиболее эффективно, когда идет от накопления опыта решения разнообразных задач к осознанию характеристик задач и процесса решения задач; от применения или наблюдения за применением об­щих приемов и методов на интуитивном уровне к осознанию и обоб­щению их, к учебной деятельности по овладению ими.

Ребенок, поступающий в школу, уже имеет опыт решения задач, в том числе и простейших арифметических, на основе интуитивной догадки, с помощью предметных действий. У одних детей этот опыт богаче, у других — беднее. В большинстве случаев он не осознан ими. Начинать обучение нужно с обогащения этого опыта. Важное место при этом занимает операция сравнения. С первых уроков детей нужно учить наблюдать мир, сравнивать предметы и группы предметов по са­мым разнообразным свойствам, классифицировать объекты окружаю­щего мира, организовывать обсуждение способов обозначения свойств, сходства и различий, установленных по какому-либо признаку отно­шений равенства и неравенства, отношений целого и части.

Основная цель первого периода обучения решению задач — фор­мирование у учащихся основных познавательных действий, пред­ставлений о ключевых отношениях мира: целого и части, равенства и неравенства, числах и действиях с ними.

Если учитель (а вслед за ним и учащиеся) будет использовать сло­во «задача» с первых уроков обучения математике, то через некото­рое время можно будет ввести и понятие, как обобщение тех задач, которые дети уже встречали на уроках и даже решали перечнем сле­дующих вопросов: • Знакомо ли вам слово «задача»? (Да.) • В каких ситуациях мы им пользовались? …• Сегодня в начале урока вы ре­шали такую задачу: …• Какие еще задачи вы помните? …• Что есть в каждой задаче? …

При таком введении понятия «задача» учащиеся сами в результа­те сопоставления задач смогут выделить части задачи. Учитель лишь должен сообщить общепринятые названия частей — условие и тре­бование (вопрос).

Решение задачи. Термин решение задачи употребляется в четы­рех разных значениях¹: 1. Процесс перехода от условия к выполнению требования задачи (к ответу на вопрос задачи). 2. Запись результата процесса решения. (Покажи мне свое решение.). 3. Ответ на вопрос задачи или вывод о выполнении требования (Назови свое решение).

¹ Фридман Л.М. Логико-психологический анализ школьных учебных за­дач. — М.: Педагогика, 1977.

214

4. Способ, метод перехода от условия к выполнению требования за­дачи (Какое красивое решение найдено!). Значение термина обычно ясно из контекста. В обучении младших школьников этот термин нужно использовать так, чтобы его смысл был ясен.

Процесс решения задачи может проходить развернуто с обо­снованием каждого шага или свернуто; вербально (со словесным оформлением) или не вербально (без словесного выражения); путем последовательного логического вывода или на основе интуиции, когда ответ на вопрос возникает в результате озарения (догадки).

Невербальное решение осуществляется на основе зрительных, слу­ховых, осязательных или кинестетических образов. Такое решение не всегда удается описать, но его нужно признавать, учить рефлексии, учить выражать в слове, рисунке, математической записи, учить на­ходить другие решения, лучше поддающиеся представлению вовне.

В начальной школе необходимо обеспечить учащимся возможность решения с любыми названными характеристиками. Это позволит развивать соответствующие способности детей. Можно, например, проводить специальные уроки обучения умению представлять способ решения устно, письменно, графически, «предметно» (через действия с предметами), конкурсы на самое лучшее устное, письменное, пред­метное, графическое представление способа решения. Полезно про­водить «блиц-решения» (Л. Г. Петерсон) — быстрые решения.

Для изучения процесса решения задачи исследователи наблюдали за своими решениями и решениями других, за процессом обучения решению задач. Одним из результатов было выделение этапов (дей­ствий) решения задачи. Известно несколько перечней этапов, раз­личия между которыми состоят в мере дробления процесса решения, в определении границ между этапами.

Исходя из особенностей решения задач учащимися начальной школы и целей формирования у них умения решать задачи; выде­ляют пять этапов: 1) восприятие и осмысление (анализ) задачи; 2) поиск путей решения и составление плана решения; 3) выполнение плана решения, формулирование вывода о выполнении требования задачи (ответа на вопрос задачи); 4) проверка, обоснование реше­ния; 5) формулирование вывода о выполнении требования задачи (ответа на вопрос задачи).

Отметим, что выделение этапов является условным. В реальном процессе решения нет четко обозначенных границ между этапами. Он только начинается всегда с восприятия ситуации (на основе которой формулируется задача), а далее может проходить в любом порядке, например продолжиться подбором ответа и его проверкой. Составле­ние плана решения часто происходит одновременно с осмыслением (анализом) задачи и выполнением плана, а проверка наиболее эф­фективна, когда она предваряет и сопровождает решение.

При контроле решения часто возникает вопрос: когда считать задачу решенной. На этот вопрос имеется два ответа:

215

1. задача считается решенной, если выполнено требование за­дачи (дан ответ на вопрос), соответствующий условию задачи и исчерпывающий все возможные варианты. Если задача допуска­ет несколько или много разных ответов, удовлетворяющих задаче, то она считается решенной, когда найдены все ее решения. Зада­чу можно считать частично решенной, если найдены не все реше­ния. Задача: «Какой улов мог быть у Коли, если он был больше чем у Димы, но меньше чем у Олега, которые поймали соответственно 5 рыб и 9 рыб?» Полный ответ: «Улов Коли мог составить 6, 7 или 8 рыб. Частичное решение: «Улов Коли мог составить 7 рыб»;

2. задача считается решенной, когда представлен и обоснован способ ее  решения и результат.

Второй ответ характерен для математики, так как математика представляет собой ту сферу деятельности, где разрабатывают спосо­бы решения. В математике важен способ решения, а не ответ на во­прос конкретной задачи. Потому в математике и существует дого­воренность: считать задачу решенной только при представлении обоснованного способа решения. Знакомить с таким пониманием понятия «решить задачу» нужно именно как с договоренностями. И обсуждать причины, по которым эти договоренности возникли. Необходимо обсуждать также вопросы о том, когда при изучении математики решение задачи нужно оформлять и представлять раз­вернуто, с обоснованием, а когда полезным и эффективным для формирования умения решать задачи будет решение без письмен­ного оформления. (Так, устное решение без оформления способа решения может быть полезно для развития интуиции, обнаружения трудностей решения, открытия новых решений.)

Научить учащихся решать задачи — значит ознакомить их с эта­пами и инструментарием решения любых задач и задач некоторых ба­зовых видов, приемами, помогающими решению, с методами и спо­собами решения, создать условия для овладения каждым учащимся в соответствии с его особенностями и возможностями достаточным количеством таких приемов, методов и способов.

Средством формирования представлений о процессе решения, знаний об этапах решения любой задачи может быть рефлексивный анализ учащимися собственного процесса решения. Для его органи­зации учитель периодически заставляет учащихся проводить анализ того, что они сделали, как сделали и в каком порядке делали, чтобы решить задачу. Это помогает учащимся понять и процесс решения задачи, и себя в нем.

После накопления впечатлений и информации от проведенного анализа, полезно проведение специальных уроков по теме «Как мы решаем задачи». Предметом обсуждения и осознания на таких уроках является процесс решения задачи: дети ищут ответ на вопрос темы урока. Форма проведения уроков — диалоговая. Здесь важен процесс обсуждения, попытки каждого ребенка развернуть исходный вопрос

216

в другие: «Почему одни задачи решаются, а другие — нет?», «Чем отличается процесс успешного решения от неуспешного?», «С чего нужно начинать решение задачи?» и др. Нужно каждому предоставить возможность сформулировать свои вопросы, свои версии ответов.

В результате обсуждения учащиеся приходят к выводу: для того что­бы решить задачу, нужно: • понять ее (понять смысл каждого слова, зна­ка в тексте задачи; понять, что о чем и как сказано, что от чего зависит; о чем задача, что спрашивается, что про это известно и неизвестно); • наметить что и в какой последовательности делать, чтобы ответить на вопрос задачи; • выполнить намеченный план, ответить на вопрос (сформулировать вывод о выполнении требования) задачи; • проверить правильность результата и хода решения; • сделать вывод.

При выделении этапов решения важно понять задачу, понима­ние является необходимым, а иногда и достаточным условием успеш­ности наших усилий по решению задачи. Вне понимания решение не может быть успешным, поэтому, приступая к решению задачи, полезно задать вопросы: «Что это за задача? О чем она? Что обо­значает слово …, число …, словосочетание…, предложение …? Что спрашивается?» и др.

Значимый ракурс понимания решения задачи заключается в со­поставлении вопросов: «Что значит решить (решать) задачу?» и «Как можно решить (решать) задачу?» и ответов на них. Лишь ответив на вопросы первой группы, можно перейти к вопросам «Как решить эту задачу?» и «Что делать и в какой последовательности, чтобы выполнить требование?»

Ответы на первую группу вопросов характеризуют смысл про­цесса решения задачи. Этот смысл остается неизменным для всех задач, методов и способов решений: решить задачу — значит най­ти ответ на вопрос (выполнить ее  требование) и способ решения. На вопрос «Как решить (решать) задачу?» однозначного ответа нет. Путей, методов, способов, приемов перехода от условия к вы­полнению требования задачи существует много для любой задачи. Различие вопросов «Что это?» и «Как действовать?» нужно донести до каждого учащегося.

Возможность разных ответов на вопрос: «Как решать задачу?» по­буждает детей к экспериментированию, догадкам, идеям решений, изобретению способов решения. Если знаешь, что существует много путей решения, стоит ли огорчаться, что забыл один путь? Что зна­чит один забытый путь в сравнении со многими другими, которые можно найти самому! Это мощная мотивационная посылка. Дети, принявшие ее, чувствуют силу своего ума, не боятся нестандартных решений. Им открыты радость познания и понимания, возможность получить удовольствие от умственной работы.

У учителя, допускающего и поддерживающего многообразие пу­тей, способов и форм решения, учащиеся всегда заняты, не боятся забыть показанный им или освоенный способ, и на каждом уроке го-

217

товы к открытиям. Эта позиция решает и проблему разноуровневого обучения. Одна и та же задача за одно и то же время разными уча­щимися может быть решена разным числом способов в соответствии с уровнем своих способностей и работоспособности на конкретном уроке: сколько детей — столько и уровней. По одной и той же задаче разными учащимися могут быть выполнены разные задания и раз­ное их количество (решить и сравнить разные методы и способы ре­шения, преобразовать задачу из одного вида в другой, представить разные формы записи, сформулировать подзадачи и др.) Освоение учащимися знаний об этапах и приемах их выполнения, о методах и способах решения происходит одновременно с обучением умению пользоваться этими приемами, методами и способами.