
- •Контрольная работа . Семестр 3.
- •По математическому анализу для бакалавров 2 курса специальности «математика с доп. Спец.»
- •Всего 20 вариантов. Выполненную работу сдать 25 декабря.
- •Вариант № 1
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Вариант № 6
- •Вариант № 7
- •Вариант № 8
- •Вариант № 9
- •Вариант № 10
- •Вариант № 11
- •Вариант № 12
- •Вариант № 13
- •Вариант № 14
- •Вариант № 15
- •Вариант № 16
- •Вариант № 17
- •Вариант № 18
- •Вариант № 19
- •Вариант № 20
Вариант № 8
Найти предел функции или доказать, что он не существует
1)
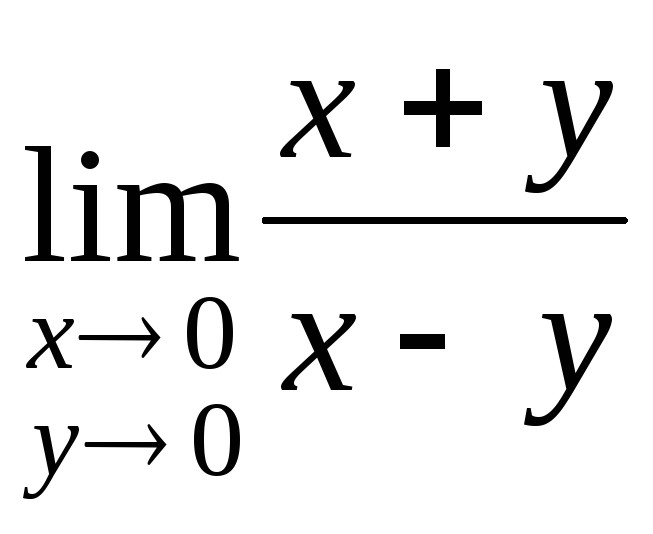 ;
2)
;
2)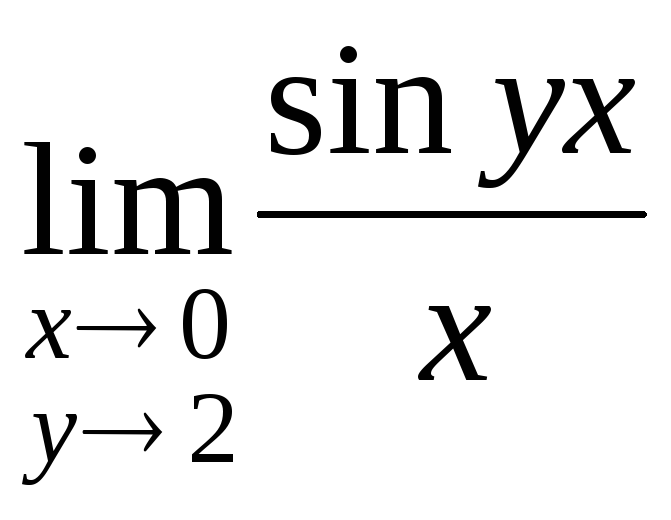 .
.
3) Найти все частные
производные второго порядка от функции
![]() .
.
Найти указанные частные производные сложной функции
4)
![]() ;
;![]() ?
?![]() ?
?![]() ?
?
5)
![]() ;
;![]() ?
?
6)
![]() ,
,![]() ?
?
7) Функция
![]() задана неявно уравнением
задана неявно уравнением![]() .
Найти
.
Найти![]() .
.
8) Функция
![]() задана неявно уравнением
задана неявно уравнением![]() .
Найти
.
Найти![]() и
и![]() .
.
9) Для функции
![]() найти:
найти:
а) производную в
точке
![]() в направлении, образующим с осями
координат углы 600, 450и 600соответственно;
в направлении, образующим с осями
координат углы 600, 450и 600соответственно;
б) graduв точкеN(2,1,1).
10) Записать
уравнения касательной плоскости и
нормали к поверхности
![]() в точке
в точке![]() .
Существует ли на поверхности точка, в
которой нормаль к поверхности параллельна
осиOY?
.
Существует ли на поверхности точка, в
которой нормаль к поверхности параллельна
осиOY?
11) Исследовать на
экстремум функцию
![]() .
.
12) Записать формулу
Тейлора до членов 2-го порядка малости
для функции
![]() в окрестности точки М(1,1,0).
в окрестности точки М(1,1,0).
13) Исследовать
функцию
![]() на непрерывность и дифференцируемость
в точке М(0;0).
на непрерывность и дифференцируемость
в точке М(0;0).
14) Найти наибольшее
и наименьшее значения функции
![]() в области, ограниченной кривыми
в области, ограниченной кривыми![]() .
.
15) Вычислить
приближённо
![]() .
.
Вариант № 9
Найти предел функции или доказать, что он не существует
1)
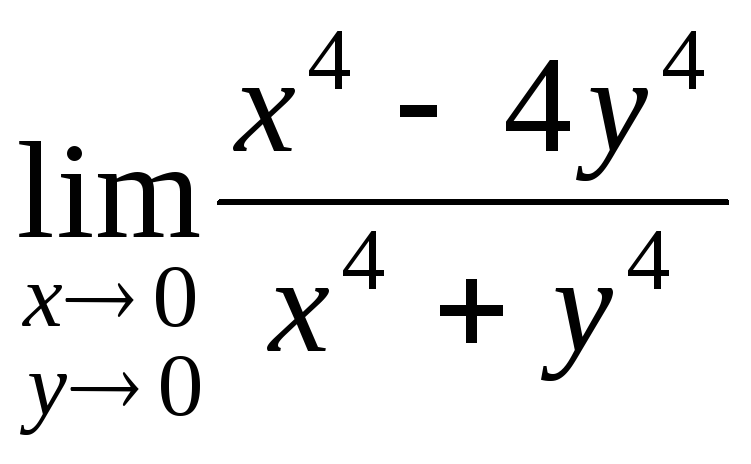 ;
2)
;
2)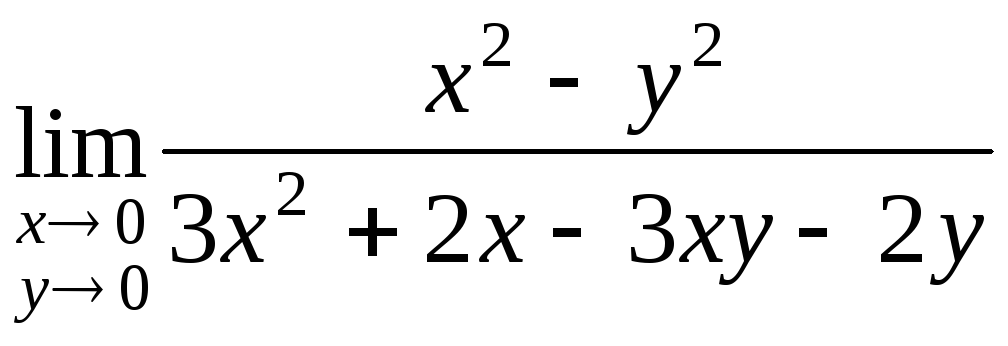 .
.
3) Найти все частные
производные второго порядка от функции
![]() .
.
Найти указанные частные производные сложной функции
4)
![]() ;
;![]() ?
?![]() ?
?![]() ?
?
5)
![]() ;
;![]() ?
?
6)
![]() ,
,![]() ?
?
7) Функция
![]() задана неявно уравнением
задана неявно уравнением![]() .
Найти
.
Найти![]() .
.
8) Функция
![]() задана неявно уравнением
задана неявно уравнением![]() .
Найти
.
Найти![]() и
и![]() .
.
9) Для функции
![]() найти:
найти:
а) производную в точке М(1,1) в направлении биссектрисы первого координатного угла;
б) gradzв точкеN(1,0).
10) Записать уравнения
касательной плоскости и нормали к
поверхности
![]() в точкеМ(1,1,1). Существует ли на
поверхности точка, в которой нормаль
к поверхности параллельна осиOZ?
в точкеМ(1,1,1). Существует ли на
поверхности точка, в которой нормаль
к поверхности параллельна осиOZ?
11) Исследовать на
экстремум функцию
![]() .
.
12) Записать формулу
Тейлора до членов 2-го порядка малости
для функции
![]() в окрестности точки М(1,0,1).
в окрестности точки М(1,0,1).
13) Исследовать
функцию
![]() на непрерывность и дифференцируемость
в точке М(0;0).
на непрерывность и дифференцируемость
в точке М(0;0).
14) Найти наибольшее
и наименьшее значения функции
![]() в круге
в круге![]() .
.
15) Вычислить
приближённо
![]() .
.
Вариант № 10
Найти предел функции или доказать, что он не существует
1)
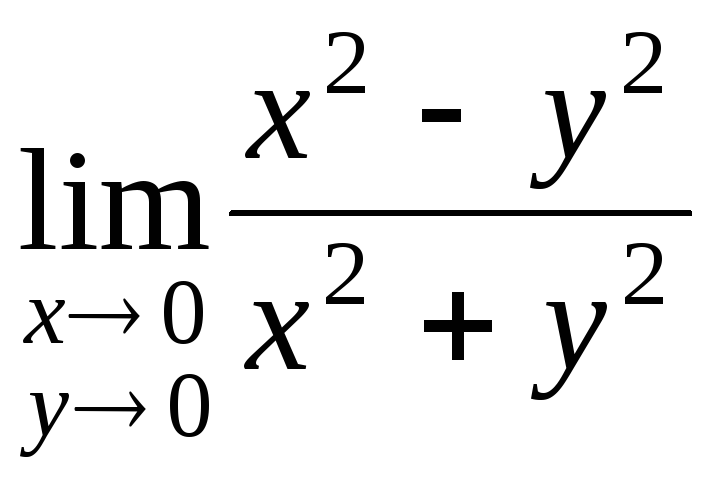 ;
2)
;
2)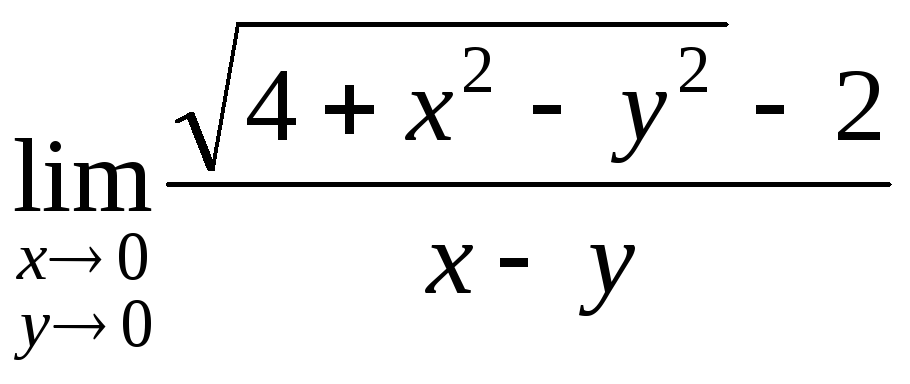 .
.
3) Найти все частные
производные второго порядка от функции
![]() .
.
Найти указанные частные производные сложной функции
4)
![]() ;
;![]() ?
?![]() ?
?![]() ?
?
5)
![]() ;
;![]() ?
?
6)
![]() ,
,![]() ?
?
7) Функция
![]() задана неявно уравнением
задана неявно уравнением![]() .
Найти
.
Найти![]() .
.
8) Функция
![]() задана неявно уравнением
задана неявно уравнением![]() .
.
Найти
![]() и
и![]() .
.
9) Для функции
![]() найти:
найти:
а) производную в
точке М(1,2) в направлении, составляющем
с осью![]() угол в 600, а с осью
угол в 600, а с осью![]() –
тупой угол;
–
тупой угол;
б) gradzв точкеN(2,1).
10) Записать
уравнения касательной плоскости и
нормали к поверхности
![]() в точкеМ(-2,1,1). Существует ли на
поверхности точка, в которой нормаль к
поверхности параллельна осиOZ?
в точкеМ(-2,1,1). Существует ли на
поверхности точка, в которой нормаль к
поверхности параллельна осиOZ?
11) Исследовать на
экстремум функцию
![]() .
.
12) Записать формулу
Тейлора до членов 2-го порядка малости
для функции
![]() в окрестности точки М(1,0,1).
в окрестности точки М(1,0,1).
13) Исследовать
функцию
![]() на непрерывность и дифференцируемость
в точке М(0;0).
на непрерывность и дифференцируемость
в точке М(0;0).
14) Найти наибольшее
и наименьшее значения функции
![]() в круге
в круге![]() .
.
15) Вычислить
приближённо
![]() .
.
Вариант № 11
Найти предел функции или доказать, что он не существует
1)
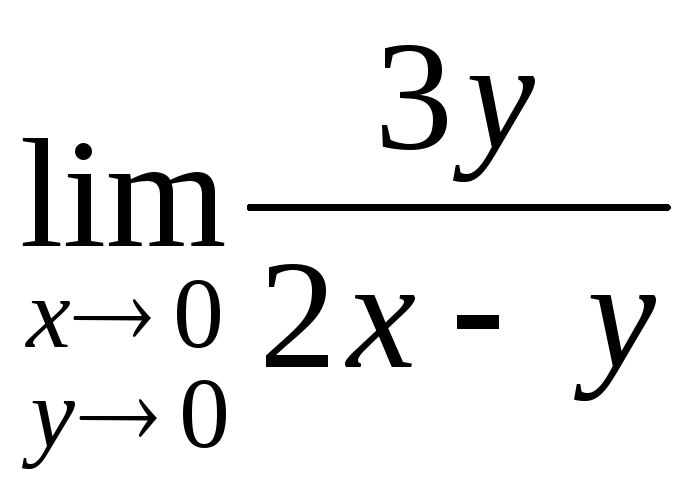 ;
2)
;
2)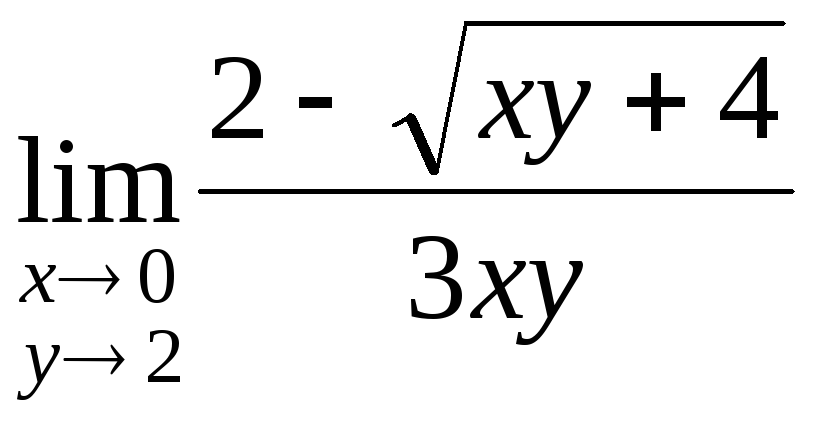 .
.
3) Найти все частные
производные второго порядка от функции
![]() .
.
Найти указанные частные производные сложной функции
4)
![]() ;
;![]() ?
?![]() ?
?![]() ?
?
5)
![]() ;
;![]() ?
?
6)
![]() ,
,![]() ?
?
7) Функция
![]() задана неявно уравнением
задана неявно уравнением![]() .
Найти
.
Найти![]() .
.
8) Функция
![]() задана неявно уравнением
задана неявно уравнением![]() .
Найти
.
Найти![]() и
и![]() .
.
9) Для функции
![]() найти:
найти:
а) производную в
точке О(0,0) в направлении вектора![]() ;
;
б) gradzв точкеN(1,1).
10) Записать уравнения
касательной плоскости и нормали к
поверхности
![]() в точкеМ(1,1,1). Существует ли на
поверхности точка, в которой касательная
плоскость к поверхности параллельна
плоскостиXOY?
в точкеМ(1,1,1). Существует ли на
поверхности точка, в которой касательная
плоскость к поверхности параллельна
плоскостиXOY?
11) Исследовать на экстремум функцию
![]() .
.
12) Записать формулу
Тейлора до членов 2-го порядка малости
для функции
![]() в окрестности точки М(,0).
в окрестности точки М(,0).
13) Исследовать
функцию
![]() на непрерывность и дифференцируемость
в точке М(0;0).
на непрерывность и дифференцируемость
в точке М(0;0).
14) Найти наибольшее
и наименьшее значения функции
![]() в области
в области![]() .
.
15) Вычислить
приближённо значение функции
![]() в точкеМ(2,04;2,95).
в точкеМ(2,04;2,95).
