
Транспортная задача
На трех станциях отправления имеется соответственно 30, 50, и 20 ед. однородного груза, который нужно доставить в четыре пункта назначения согласно их потребностям. Эти данные, а также стоимость перевозки единицыгруза от каждой станции отправления к каждому пункту назначения указаны в таблице. Составить план перевозок грузов, чтобы затраты на эти перевозки были минимальными.
|
Пункты отправления |
Запасы груза |
Пункты назначения
| |||
|
|
|
|
| ||
|
|
30 |
1 |
8 |
2 |
3 |
|
|
50 |
4 |
7 |
5 |
1 |
|
|
20 |
5 |
3 |
4 |
4 |
|
Потребности |
15 |
35 |
40 |
30 | |
Решение.
Этап 1.
Часто условие транспортной задачи оформляют матрицей:
|
1 |
8 |
2 |
3 |
30 |
|
4 |
7 |
5 |
1 |
50 |
|
5 |
3 |
4 |
4 |
20 |
|
15 |
35 |
40 |
30 |
|
Построим математическую модель транспортной задачи.
1. «Составить
план перевозок грузов» - значит определитьсколько, от куда и куданадо перевезти
груза, чтобы достичь поставленной цели
- «затраты на эти перевозки были
минимальными». Введем управляющие
переменные: - количество груза, перевозимого из
пункта
- количество груза, перевозимого из
пункта в пункт
в пункт (
( ).
).
2.Стоимость
этой перевозки составит .
Тогда целевая функция - суммарные
затраты, связанные с реализацией всего
плана перевозок – запишется выражением:
.
Тогда целевая функция - суммарные
затраты, связанные с реализацией всего
плана перевозок – запишется выражением:
в
общем виде
 ,
где
,
где
в
нашей задаче

Для построения системы ограничений проверим, является ли задача сбалансированной.
|
Суммарная
мощность поставщиков Суммарная мощность потребителей |
|
Следовательно, условие сбалансированности не выполнено.
4.Запишем систему ограничений:
По
потребителю: мощности поставщиков
меньше мощности потребителей,
следовательно, кто-то из потребителей
получит груза меньше, чем его потребность .
.
Количество
груза, которое потребитель
 действительно получит запишется
выражением:
действительно получит запишется
выражением: .
Так как это меньше, чем его потребность,
ограничение будет иметь вид:
.
Так как это меньше, чем его потребность,
ограничение будет иметь вид: .
.
Аналогично
строятся ограничения по другим
потребителям. Так как в задаче заранее
не оговаривается, потребности какого
потребителя не будут удовлетворены,
знак
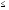 поставим в ограничениях по всем
потребителям. Получим систему ограничений
по потребителю:
поставим в ограничениях по всем
потребителям. Получим систему ограничений
по потребителю:

По
поставщику:весь имеющийся на
станции отправления груз будет вывезен
(т.е. ):
):
 ;
;
Прямые
ограничения
 .
.
Этап 2.
1.Подготовим форму для ввода исходных данных (Рис 15.),
В нашем примере матрица затрат по
доставке груза с конкретной станции
отправления каждому потребителю
 вводится в ячейки блока В3:E5.
В ячейках В6:E6 указываются
потребности
вводится в ячейки блока В3:E5.
В ячейках В6:E6 указываются
потребности в пунктах назначения
в пунктах назначения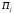 ,
мощности
,
мощности поставщиков
поставщиков записаны в блокеF3:F5.
записаны в блокеF3:F5.
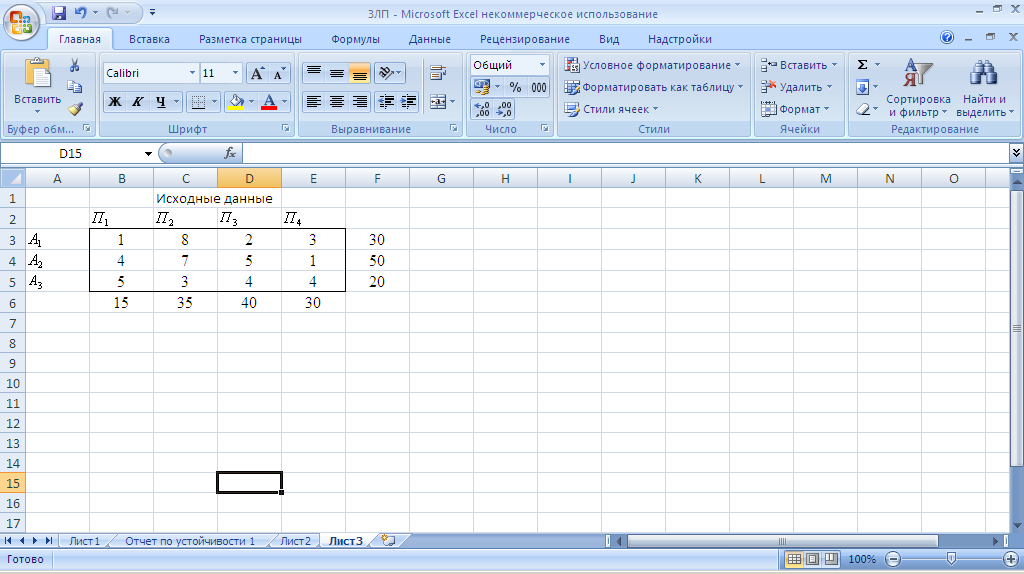
Рис. 15 Ввод исходных данных.
2.Зарезервируем изменяемые ячейки,
в которых после решения задачи будет
находиться оптимальный план перевозок .
Размерность этого массиваобязательнодолжна совпадать с размерностью матрицы
затрат: выделим блок ячеекI3:L5
(можно ввести в эти ячейки «1» ) (рис.
16).
.
Размерность этого массиваобязательнодолжна совпадать с размерностью матрицы
затрат: выделим блок ячеекI3:L5
(можно ввести в эти ячейки «1» ) (рис.
16).

Рис 16. Создание формы для ввода условий задачи.
Введем зависимость для целевой функции(рис. 17). Оптимальное значение целевой функции будет помещено в ячейке В8:
Курсор в ячейку В8
 .
.Мастер функций fx / Математические / СУММПРОИЗВ(В3:E5;I3:L5)

Рис. 17 Ввод зависимости для целевой функции
Введем зависимости ограничений, стоящие в левых частях ограничений.
- вводим условия реализации мощностей поставщиков(рис 18.):
Курсор в ячейку М3.

Мастер функций fx / Математические / СУММ(I3:L3)
Курсор в ячейку М3.
Растянуть (копировать) ячейку М3 в ячейки М4 и М5.

Рис. 18. Ввод зависимостей ограничений по поставщикам.
- вводим зависимостей ограничений по потребителям(рис. 19):
курсор в ячейку I6.
 ;
;
Мастер функций fx / Математические / СУММ(I3:I5)
Курсор в ячейку I6.
Растянуть (копировать) ячейку I6 в ячейкиJ6,K6 иL6.

Рис. 19. Ввод зависимостей ограничений по потребителям.
На этом ввод зависимостей закончен.
Этап 3. Запуск программы Поиск решений
После выбора команд Поиск решенияпоявится диалоговое окно Поиск решения.
Назначение целевой ячейки: курсор в поле Установить целевую ячейку.
 .
Левой кнопкой мыши щелкнуть на ячейке
В8.
.
Левой кнопкой мыши щелкнуть на ячейке
В8.Ввести направление целевой функции: минимальному значению.
Ввести адреса искомых переменных: курсор в поле Изменяя ячейки.
 .
Выделить мышью адреса ячеекI3:L5.
.
Выделить мышью адреса ячеекI3:L5.Ввести ограничения:
курсор в поле Ограничения
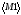 .
Выбрать режимДобавить
.
Выбрать режимДобавить .
.курсор в поле Ссылка на ячейку

выбрать мышью ячейки I6:L6
ввести знак ограничения <=
курсор в правое окно Ограничение
 .
.указать мышью адреса В6:E6

Остальные ограничения ввести аналогично. В результате этих действий окно Поиск решенийбудет выглядеть, как представлено на рис 20.

Рис. 20. Введены все ограничения.
Выбрать параметрымодели: рис 4.
Этап 4. Выполнить.
На экране диалоговое окно Результат поиска решения (рис.18.) .

Рис.21. Решение найдено.
Найденный план перевозок означает, что общая стоимость перевозок составит 235 ден.ед., если
 ед.
груза перевести со станции 1 потребителю
3;
ед.
груза перевести со станции 1 потребителю
3;
 ед.
груза перевести со станции 2 потребителю
1;
ед.
груза перевести со станции 2 потребителю
1;
 ед.
груза перевести со станции 2 потребителю
3;
ед.
груза перевести со станции 2 потребителю
3;
 ед.
груза перевести со станции 2 потребителю
4;
ед.
груза перевести со станции 2 потребителю
4;
 ед.
груза перевести со станции 3 потребителю
2.
ед.
груза перевести со станции 3 потребителю
2.
Неудовлетворены
будут потребители
 и
и ,
т.к. они получат груза меньше, чем
составляют их потребности. Так, например,
потребность
,
т.к. они получат груза меньше, чем
составляют их потребности. Так, например,
потребность составляет 35 ед. груза (ячейкаC6),
а получит он только 20 ед. (ячейкаJ6).
составляет 35 ед. груза (ячейкаC6),
а получит он только 20 ед. (ячейкаJ6).
Остальные потребители удовлетворены полностью.
Вопросы:
Сколько груза должно быть перевезено из А2 в П1?
С кем работает поставщик А2?
С кем работает потребитель П4?
Измените модель, добавив условие:
Потребности П2 обязательно должны быть удовлетворены. (F=265)
Запрещены перевозки в направлении А2 –П3.(F=245)
В направлении А3—П1 необходимо перевезти не менее 5 тонн.(F=250)
Возможности А3 стали равны 50; (F=290)





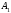

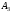
 ед
ед
