Embedded Robotics (Thomas Braunl, 2 ed, 2006)

Mobile robot competitions have been around for over 20 years, with the Micro Mouse Contest being the first of its kind in 1977. These competitions have inspired generations of students, researchers, and laypersons alike, while consuming vast amounts of research funding and

personal time and effort. Competitions provide a goal together with an objective performance measure, while extensive media coverage allows participants to present their work to a wider forum.

As the robots in a competition evolved over the years, becoming faster and smarter, so did the competitions themselves. Today, interest has shifted from the “mostly solved” maze contest toward robot soccer (see Chapter 18).

15.1 Micro Mouse Contest

217217

15 Maze Exploration

Figure 15.1: Maze from Micro Mouse Contest in London 1986

would find the goal by always following the left (or the right) wall. A few of these scored even higher than some of the intelligent mice, which were mechanically slower.

John Billingsley [Billingsley 1982] made the Micro Mouse Contest popular in Europe and called for the first rule change: starting in a corner, the goal should be in the center and not in another corner, to eliminate wall huggers. From then on, more intelligent behavior was required to solve a maze (Figure 15.1). Virtually all robotics labs at that time were building micromice in one form or another – a real micromouse craze was going around the world. All of a sudden, people had a goal and could share ideas with a large number of colleagues who were working on exactly the same problem.

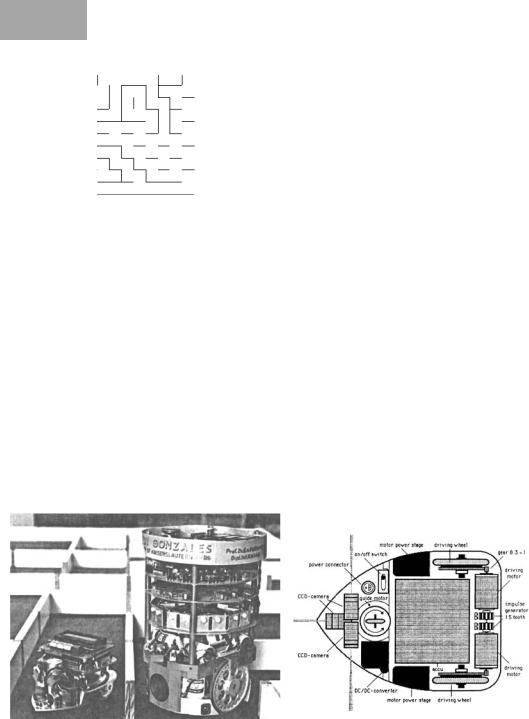
Figure 15.2: Two generations of micromice, Univ. Kaiserslautern

Micromouse technology evolved quite a bit over time, as did the running time. A typical sensor arrangement was to use three sensors to detect any walls in front, to the left, and to the right of the mouse. Early mice used simple

218

Maze Exploration Algorithms

micro-switches as touch sensors, while later on sonar, infrared, or even optical sensors [Hinkel 1987] became popular (Figure 15.2).

While the mouse’s size is restricted by the maze’s wall distance, smaller and especially lighter mice have the advantage of higher acceleration/deceleration and therefore higher speed. Even smaller mice became able to drive in a straight diagonal line instead of going through a sequence of left/right turns, which exist in most mazes.

Figure 15.3: Micromouse, Univ. of Queensland

One of today’s fastest mice comes from the University of Queensland, Australia (see Figure 15.3 – the Micro Mouse Contest has survived until today!), using three extended arms with several infrared sensors each for reliable wall distance measurement. By and large, it looks as if the micromouse problem has been solved, with the only possible improvement being on the mechanics side, but not in electronics, sensors, or software [Bräunl 1999].

15.2 Maze Exploration Algorithms

For maze exploration, we will develop two algorithms: a simple iterative procedure that follows the left wall of the maze (“wall hugger”), and an only slightly more complex recursive procedure to explore the full maze.

15.2.1 Wall-Following

Our first naive approach for the exploration part of the problem is to always follow the left wall. For example, if a robot comes to an intersection with several open sides, it follows the leftmost path. Program 15.1 shows the implementation of this function explore_left. The start square is assumed to be at position [0,0], the four directions north, west, south, and east are encoded as integers 0, 1, 2, 3.

The procedure explore_left is very simple and comprises only a few lines of code. It contains a single while-loop that terminates when the goal square is

219

15 Maze Exploration

Program 15.1: Explore-Left

1void explore_left(int goal_x, int goal_y)

2{ int x=0, y=0, dir=0; /* start position */

3int front_open, left_open, right_open;

4

5while (!(x==goal_x && y==goal_y)) /* goal not reached */

6{ front_open = PSDGet(psd_front) > THRES;

15}

16}

reached (x and y coordinates match). In each iteration, it is determined by reading the robot’s infrared sensors whether a wall exists on the front, left-, or right-hand side (boolean variables front_open, left_open, right_open). The robot then selects the “leftmost” direction for its further journey. That is, if possible it will always drive left, if not it will try driving straight, and only if the other two directions are blocked, will it try to drive right. If none of the three directions are free, the robot will turn on the spot and go back one square, since it has obviously arrived at a dead-end.

Program 15.2: Driving support functions

1 void turn(int change, int *dir)

2 { VWDriveTurn(vw, change*PI/2.0, ASPEED);

3VWDriveWait(vw);

4*dir = (*dir+change +4) % 4;

5}

1void go_one(int *x, int *y, int dir)

2{ switch (dir)

3{ case 0: (*y)++; break;

4case 1: (*x)--; break;

5case 2: (*y)--; break;

6case 3: (*x)++; break;

7}

8VWDriveStraight(vw, DIST, SPEED);

9VWDriveWait(vw);

10}

The support functions for turning multiples of 90° and driving one square are quite simple and shown in Program 15.2. Function turn turns the robot by the desired angle (r90° or 180°), and then updates the direction parameter dir.

220

Maze Exploration Algorithms

Function go_one updates the robot’s position in x and y, depending on the current direction dir. It then drives the robot a fixed distance forward.

This simple and elegant algorithm works very well for most mazes. However, there are mazes where this algorithm does not work As can be seen in Figure 15.4, a maze can be constructed with the goal in the middle, so a wallfollowing robot will never reach it. The recursive algorithm shown in the following section, however, will be able to cope with arbitrary mazes.

Figure 15.4: Problem for wall-following

15.2.2 Recursive Exploration

The algorithm for full maze exploration guarantees that each reachable square in the maze will be visited, independent of the maze construction. This, of course, requires us to generate an internal representation of the maze and to maintain a bit-field for marking whether a particular square has already been visited. Our new algorithm is structured in several stages for exploration and navigation:

1.Explore the whole maze:

Starting at the start square, visit all reachable squares in the maze, then return to the start square (this is accomplished by a recursive algorithm).

2.Compute the shortest distance from the start square to any other square by using a “flood fill” algorithm.

3.Allow the user to enter the coordinates of a desired destination square: Then determine the shortest driving path by reversing the path in the flood fill array from the destination to the start square.

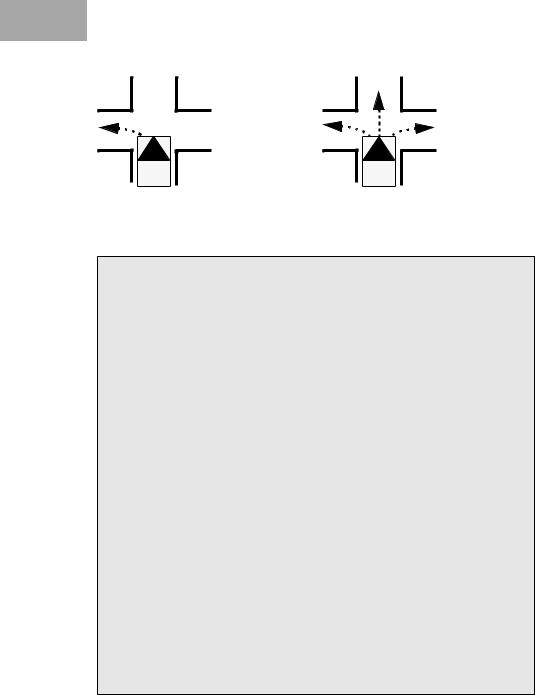
The difference between the wall-following algorithm and this recursive exploration of all paths is sketched in Figure 15.5. While the wall-following algorithm only takes a single path, the recursive algorithm explores all possible paths subsequently. Of course this requires some bookkeeping of squares already visited to avoid an infinite loop.

Program 15.3 shows an excerpt from the central recursive function explore. Similar to before, we determine whether there are walls in front and to the left and right of the current square. However, we also mark the current square as visited (data structure mark) and enter any walls found into our inter-

221

15 Maze Exploration

Figure 15.5: Left wall-following versus recursive exploration

Program 15.3: Explore

1void explore()

2{ int front_open, left_open, right_open;

3int old_dir;

6PSDGet(psd_left), PSDGet(psd_right));

7front_open = PSDGet(psd_front) > THRES;

11maze_entry(rob_x,rob_y,(rob_dir+1)%4, left_open);

12maze_entry(rob_x,rob_y,(rob_dir+3)%4, right_open);

13old_dir = rob_dir;

18go_to(old_dir+2); /* go 1 back */

19}

20if (left_open && unmarked(rob_y,rob_x,old_dir+1))

21{ go_to(old_dir+1); /* go 1 left */

23go_to(old_dir-1); /* go 1 right */

24}

25if (right_open && unmarked(rob_y,rob_x,old_dir-1))

26{ go_to(old_dir-1); /* go 1 right */

28go_to(old_dir+1); /* go 1 left */

29}

30}

nal representation using auxiliary function maze_entry. Next, we have a maximum of three recursive calls, depending on whether the direction front, left, or right is open (no wall) and the next square in this direction has not been visited before. If this is the case, the robot will drive into the next square and the procedure explore will be called recursively. Upon termination of this call, the robot will return to the previous square. Overall, this will result in the robot

222

Maze Exploration Algorithms

exploring the whole maze and returning to the start square upon completion of the algorithm.

A possible extension of this algorithm is to check in every iteration if all surrounding walls of a new, previously unvisited square are already known (for example if the surrounding squares have been visited). In that case, it is not required for the robot to actually visit this square. The trip can be saved and the internal database can be updated.

..................................

._._._._._._._._._................

-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 8 9 10 11 12 13 38 39 40 -1 -1 -1 -1 -1 -1 -1 7 28 29 30 31 32 37 40 -1 -1 -1 -1 -1 -1 -1 -1

Figure 15.6: Maze algorithm output

We have now completed the first step of the algorithm, sketched in the beginning of this section. The result can be seen in the top of Figure 15.6. We now know for each square whether it can be reached from the start square or not, and we know all walls for each reachable square.

Flood fill algorithm In the second step, we want to find the minimum distance (in squares) of each maze square from the start square. Figure 15.6, bottom, shows the shortest distances for each point in the maze from the start point. A value of –1 indicates a position that cannot be reached (for example outside the maze bounda-

223

15 Maze Exploration

ries). We are using a flood fill algorithm to accomplish this (see Program 15.4).

Program 15.4: Flood fill

1 for (i=0; i<MAZESIZE; i++) for (j=0; j<MAZESIZE; j++) 2 { map [i][j] = -1; /* init */

3nmap[i][j] = -1;

4}

5map [0][0] = 0;

6nmap[0][0] = 0;

7change = 1;

8

9while (change)

10{ change = 0;

11for (i=0; i<MAZESIZE; i++) for (j=0; j<MAZESIZE; j++)

12{ if (map[i][j] == -1)

13{ if (i>0)

15{ nmap[i][j] = map[i-1][j] + 1; change = 1; }

16if (i<MAZESIZE-1)

17if (!wall[i+1][j][0] && map[i+1][j] != -1)

18{ nmap[i][j] = map[i+1][j] + 1; change = 1; }

19if (j>0)

21{ nmap[i][j] = map[i][j-1] + 1; change = 1; }

22if (j<MAZESIZE-1)

23if (!wall[i][j+1][1] && map[i][j+1] != -1)

24{ nmap[i][j] = map[i][j+1] + 1; change = 1; }

25}

26}

27for (i=0; i<MAZESIZE; i++) for (j=0; j<MAZESIZE; j++)

28map[i][j] = nmap[i][j]; /* copy back */

29}

The program uses a 2D integer array map for recording the distances plus a copy, nmap, which is used and copied back after each iteration. In the beginning, each square (array element) is marked as unreachable (–1), except for the start square [0,0], which can be reached in zero steps. Then, we run a whileloop as long as at least one map entry changes. Since each “change” reduces the number of unknown squares (value –1) by at least one, the upper bound of loop iterations is the total number of squares (MAZESIZE2). In each iteration we use two nested for-loops to examine all unknown squares. If there is a path (no wall to north, south, east, or west) to a known square (value z –1), the new distance is computed and entered in distance array nmap. Additional if-selec- tions are required to take care of the maze borders. Figure 15.7 shows the stepwise generation of the distance map.

In the third and final step of our algorithm, we can now determine the shortest path to any maze square from the start square. We already have all wall information and the shortest distances for each square (see Figure 15.6). If the

224

Maze Exploration Algorithms

Figure 15.7: Distance map development (excerpt)

user wants the robot to drive to, say, maze square [1,2] (row 1, column 2, assuming the start square is at [0,0]), then we know already from our distance map (see Figure 15.7, bottom right) that this square can be reached in five steps. In order to find the shortest driving path, we can now simply trace back the path from the desired goal square [1,2] to the start square [0,0]. In each step we select a connected neighbor square from the current square (no wall between them) that has a distance of one less than the current square. That is, if the current square has distance d, the new selected neighbor square has to have a distance of d–1 (Figure 15.8).

Figure 15.8: Screen dumps: exploration, visited cells, distances, shortest path

Program 15.5 shows the program to find the path, Figure 15.9 demonstrates this for the example [1,2]. Since we already know the length of the path (entry in map), a simple for-loop is sufficient to construct the shortest path. In each iteration, all four sides are checked whether there is a path and the neighbor square has a distance one less than the current square. This must be the case for at least one side, or there would be an error in our data structure. There could

225

15 Maze Exploration

be more than one side for which this is true. In this case, multiple shortest paths exist.

Program 15.5: Shortest path

1void build_path(int i, int j)

2{ int k;

3for (k = map[i,j]-1; k>=0; k--)

4{

5if (i>0 && !wall[i][j][0] && map[i-1][j] == k)

6{ i--;

7path[k] = 0; /* north */

8}

9else

10if (i<MAZESIZE-1 &&!wall[i+1][j][0] &&map[i+1][j]==k)

11{ i++;

12path[k] = 2; /* south */

13}

14else

15if (j>0 && !wall[i][j][1] && map[i][j-1]==k)

16{ j--;

17path[k] = 3; /* east */

18}

19else

20if (j<MAZESIZE-1 &&!wall[i][j+1][1] &&map[i][j+1]==k)

21{ j++;

22path[k] = 1; /* west */

23}

24else

25{ LCDPutString("ERROR\a");

26}

27}

28}

15.3Simulated versus Real Maze Program

226