Федеральное агентство железнодорожного транспорта

Уральский государственный университет путей сообщения

Филиал УрГУПС в г. Нижний Тагил

Кафедра «Общепрофессиональные дисциплины»

Отчет по лабораторной работе №3

«Частично неупругие соударения шаров»

Преподаватель

Студент

Нижний Тагил

2012

1. Упругие и неупругие соударения тел (законы сохранения)

Использование закона сохранения импульса (ЗСИ) вместе с законом сохранения механической энергии (ЗСМЭ) позволяет решать более просто задачи механики, чем с использованием второго закона динамики. При соударении тела деформируют друг друга. При упругомсоударении их кинетическая энергия переходит в потенциальную энергию упругой деформации. Затем тела снова приобретают первоначальную форму, отталкивая друг друга, при этом потенциальная энергия упругой деформации переходит в кинетическую энергию и тела разлетаются.При абсолютно упругом ударе выполняется ЗСИ и ЗСМЭ. Приближения упругих соударений: столкновения молекул газа друг с другом и со стенками сосуда, в котором находится газ; рассеяние -частиц при прохождении через тонкие пленки вещества; рентгеновские кванты при взаимодействии со свободными электронами; нейтроны в ядерных реакциях.

Рассмотрим упругое соударение двух тел с массами m₁ и m₂. Обозначим скорости тел до и после удара соответственно и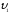',', причем тело m₂ до соударения покоится . Запишем

ЗСИ '+' (1)

ЗСМЭ m₁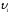² / 2 = m₁'² / 2 + m₂'² / 2 (2)

При решении системы уравнений 1 и 2 получим

'' (3)

² = '² '² (4)

Соотношение (3) показывает, что в данном случае векторы ,','образуют треугольник, а из выражения (4) следует, что этот треугольник является прямоугольным с гипотенузой . Таким образом, при соударении шаров с одинаковыми массами (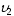= 0) они разлетаются под прямым углом.

Центральный удар шаров. Удар называется центральным, если тела до удара движутся вдоль прямой, проходящей через их центр масс. После удара шары будут двигаться по прямой в направлении скорости налетающего шара или в обратном направлении. В этом случае векторная и скалярная записи подобны. Тогда из соотношений (1) и (2) запишем

(') =' (5)

(² – '²) '² (6)

Соотношение (6) делим на (5) и получим +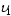' =' = 2при. Здесь– скорость движения центра масс. Следовательно,

' = (7)

'. (8)

Из (7) и (8) видно, что если массы m₁ = m₂, то '', то есть оба шара обмениваются своими скоростями. После столкновения первое тело останавливается, а второе начинает двигаться со скоростью первого, приm₁>> m₂ скорости ','. Первый шар не «почувствует» соударения со вторым и будет двигаться с той же скоростью, а второй шар будет двигаться с удвоенной скоростью. Еслиm₁ << m₂, то 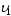' =,' = 0. Скорость массивного тела после удара практически не меняется. В результате удара стенке передается значительная доля количества движенияp₁ = 2m и небольшая часть энергии ударяющегося шара, например, удары молекул газа о стенку цилиндра или о поверхность поршня.

Закон сохранения импульса позволяет объяснить явление отдачи, при котором взаимодействующие тела приобретают равные по модулю и противоположные по направлению импульсы. Например, выстрел из орудия, реактивное движение, радиоактивный распад атомных ядер, взаимные превращения элементарных частиц.

Принцип работы лабораторной установки. В работе определяются параметры взаимодействия стальных шаров (СШ), латунных шаров (ЛШ), алюминиевых шаров (АШ). Для определения коэффициента восстановления (КВ) k шары парами СШ→СШ, АШ→АШ, ЛШ→ЛШ необходимо вставить в пружинные держатели. Держатели имеют крючки, которыми они подвешиваются к осям подвеса. Расстояние центра шара от оси подвеса равно L = 300 ± 1 мм. Кронштейн отклоняется на заданный угол и слегка зажимается винтом. Держатель маятника отклоняется на несколько больший угол, головка спускового устройства поворачивается так, чтобы соединенный с ней штырь расположился горизонтально, после чего держатель шара спускается на этот штырь. Для отпускания шара нужно повернуть головку спускового устройства на 90˚, стараясь не вызвать колебания стойки. Для снятия показаний удара шаров установите первый шар (ударяющий) в подвижной кронштейн на нужный угол начального отклонения подвеса = 40˚. Зацепите подвес шара за спусковое устройство. Повернув головку спускового устройства, освободите шар. По указанию шкалы на левой стороне определите угол отклонения второго шара (ударяемого). Относительная скорость шаров перед ударом, где, длина подвеса= 300 мм. Теоретическая зависимость времени удара от скоростимкс, гдеR – радиус шара, – скорость звука в материале шаров,– относительная скорость шаров перед ударом.

Удар абсолютно упругий, центральный. Два шара массами m₁ = m₂ радиусами подвешены в держатели шаров длинойкаждый так, что шары соприкасаются. Первый шарm₁ отклонили на высоту от положения равновесия на уголи отпустили. Высота поднятия шара. При прохождении нижней точки шары сталкиваются. Скорость первого шара перед ударом. Значения параметров для второго (ударяемого) шара сразу после упругого соударения: скорость', импульс', кинетическая энергия', угловая скорость ω', нормальное ускорение'=, максимальная высота подъема ' =, средняя сила удара первого шара, где÷мкс – время соударения шаров. Время зависит от скоростипервого шара.