Расчет и оптимизация процессов и аппаратов химических и пищевых производств в среде MatLab. Учебное пособие

Корни произвольного уравнения по заданному приближению позволяет найти встроенная функция fzero, которая вызывается следующим образом:

>> x = fzero(‘myfunction’, x0)

где ‘myfunction’ – имя файл-функции, вычисляющей левую часть уравнения; x0 – начальное приближение к корню либо вектор, содержащий концы отрезка, на котором ищутся корни; x – найденное приближенное значение корня. Данная функция находит решение с точностью до шестнадцатого знака после запятой.

Пример: Известна концентрация недиссоциированной кислоты [HA]0 – 0,1 моль–1; константа диссоциации Ka – 1,85 · 10–5; ионное произведение воды Kw – 1 · 10–14. Требуется определить кислотность рас-

десятичный логарифм концентрации ионов водорода: pH = −log(H + ) .

Функция, содержащая выражение для расчета pH, сохранена под именем concentr, а входным аргументом ее является значение концентрации ионов водорода.

function f = concentr(x)

% определение pH растворов слабых кислот

kw = 1.85e-5; ka = 1.0e-14; ha = 0.1;

f= (x^2-kw)/ka+x-(kw/x)-ha;

Впрограмме aim производится построение графика функции concentr для определения начального приближения, а затем решение нелинейного уравнения и определение pH.

%программа aim определения pH раствора

%построение графика функции для определения

%начального приближения

fplot ('concentr', [0 0.02]) grid on

%вызов fzero от файл-функции concentr, и точки приближения

%с определением значения функции в точке полученного решения

[H, f] = fzero('concentr', 0.004)

%расчет pH

pH = -log10(H)

Результаты поиска начального приближения приведены на рис. 6.2. Результаты реализации программы aim:

>> aim

H=

0.0043

f = -3.0669e-007 pH =

2.3664

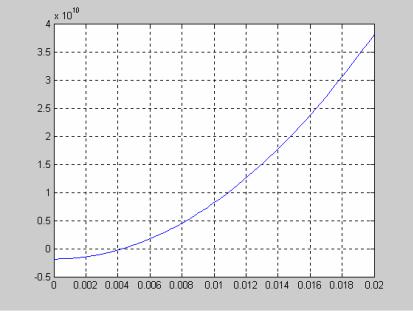
По графику легко определяется значение аргумента, близкого к нулю, которое является начальным приближением. Значение функции от полученного решения достаточно близко к нулю.

Решение систем линейных уравнений осуществляется при помощи символа «\», при этом система линейных уравнений представляется в матричном виде.

Рис. 6.2 Определение начального приближение для поиска корней уравнения

Пример: Требуется согласовать производство трех групп химических заводов, как по линии взаимных связей, так и по линии выполнения заданной им программы на производство конечной продукции. Исходные данные: программа на конечную продукцию каждой группы заводов и прогрессивные величины норм расходов этих продуктов как сырья для взаимного и собственного воспроизводства – представлены в табл. 8.

Математически согласованное производство по данным выпусков данных групп заводов с учетом прогрессивных норм расхода записывается в виде прогрессивных норм расхода или в матричной форме:

8 Исходные данные

Решим данную задачу двумя возможными способами – с использованием матричных операций и оператора «\», и произведем проверку полученного решения. Расчет материального баланса приведен в листинге программы linesist.

%задание матрицы коэффициентов и столбца свободных членов линейной системы

A = [0.92 -0.04 -0.01; -0.07 0.94 -0.02; -0.09 -0.08 0.99]; B = [50000; 30000; 80000];

%решение системы с использованием матричных операций

X1 = A^-1*B

%решение системы с использованием оператора \ X2 = A\B

%проверка правильности результатов решений

REZ1 = A*X1 % решение, полученное с помощью матричных операций

REZ2 = A*X2 % решение, полученное с помощью оператора \

Результаты реализации программы linesist:

>> linesist

X1 =

1.0e+004 *

5.6970

3.8052

8.9062

X2 =

1.0e+004 *

5.6970

3.8052

8.9062

REZ1 = 1.0e+004 * 5.0000 3.0000 8.0000

REZ2 = 1.0e+004 * 5.0000 3.0000 8.0000

6.3 Вычисление корней полинома и производных от полинома

Полином задается вектором его коэффициентов, число элементов вектора, т.е. число коэффициентов полинома всегда на единицу больше его степени, нулевые коэффициенты должны содержаться в векторе.

Вычисление значения полинома от некоторого аргумента:

>>p = [1 0 3.2 -5.2 0 0.5 1 -3];

>>polyval(p, 3)

ans =

2.5479e+003

Нахождение сразу всех корней полинома осуществляется при помощи функции roots, которая возвращает вектор корней полинома, в том числе и комплексные.

>> r = roots(p)

r =

-0.5668 + 2.0698i -0.5668 – 2.0698i -0.6305 + 0.5534i -0.6305 – 0.5534i 1.2149

0.5898 + 0.6435i

0.5898 – 0.6435i

Встроенная функция polyder предназначена для вычисления производных от полиномов. Вызов polyder с аргументом – вектором, соответствующим полиному, приводит к вычислению вектора коэффициентов производной полинома:

>>p = [1 0 1 0 0 1];

>>p1 = polyder(p)

p1 =

5 0 3 0 0

6.4 Интегрирование функций

Для вычисления интеграла используется quad, задавая первым аргументом имя файл-функции, от которой вычисляется интеграл, а вторым и третьим – нижний и верхний предел интегрирования. Данная функция вычисляет приближенное значение интеграла с точностью 10е-3.

>> I = quad('myfunction', a, b)

Пример: Вычислить летучесть аммиака f как функцию давления при заданной температуре.

Наиболее точные значения коэффициента летучести получают из экспериментальных значений коэффициента сжимаемости, определяемого из P-V-T измерений. Зависимость сжимаемости аммиака от давления определена экспериментально (табл. 9).

Для вычисления летучести как функции давления при заданной температуре используется зависимость:

где Z – функция сжимаемости газа; P – давление; f – летучесть аммиака. Вычислить летучесть и объем газа при заданных условиях.

9 Зависимость сжимаемости аммиака от давления

В функции ammiak1 записывается подынтегральная функция

function f = ammiak1(p, z)

%расчет зависимости летучести аммиака

%z – независимый параметр (летучесть) f = (z-1)./p;

Процедура ammiak рассчитывает летучесть и объем газа, результаты расчета выводятся на графики в одно окно.

%программа ammiak расчета летучести аммиака

%в зависимости от давления

%с использованием оператора for

R = 8.31514; % универсальная газовая постоянная T = 473; % температура, К

% табличные данные

P = [0.001 1 10 20 30 40 50 60 80 100 200 300 ...

400 500 600 800];

Z = [0 0.998 0.981 0.961 0.942 0.922 0.902 0.882...

0.841 0.801 0.551 0.462 0.495 0.557 0.621 0.755]; % Расчет

for i=1:length(P)

I = quad('ammiak1', 1.0e-10, P(i), [], [], Z(i)); f(i) = P(i)*exp(I); % летучесть аммиака v(i) = (Z(i)*R*T)/P(i); % объем газа

end

% графический вывод результатов subplot(3,1,1)

plot ( P, Z, 'k-')

xlabel('P')

ylabel('Z') grid on subplot(3,1,2) plot ( P, v, 'k-') xlabel('P') ylabel('v') grid on subplot(3,1,3) plot ( P, f, 'k-') xlabel('P') ylabel('f') grid on

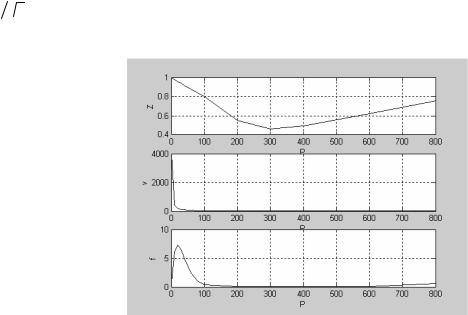
Результаты расчета на отдельных графиках представлены на рис. 6.3.

Реализованный алгоритм основан на квадратурной формуле Симпсона с автоматическим подбором шага интегрирования для достижения требуемой относительной погрешности. Интегрирование гладких функций лучше производить при помощи quad8, основанной на наиболее точных квадратурных формулах Ньютона-Котеса с автоматическим подбором шага.

При вычислении в MatLab 5.2, 5.3 интегралов от функций, имеющих интегрируемую особенность, например 1 x , в нуле выводится сообщение об ошибке. В версии 6.0 данный алгоритм улучшен для

функций с особенностями, и, кроме того, появился quadl для нахождения определенного интеграла по квадратурным формулам Гаусса-Лобатто.

Рис. 6.3 Результаты реализации программы ammiak

Также в MatLab имеются функции для вычисления двойных интегралов: dblquad. Используется следующим образом:

>> dblquad(‘myfunction’, a, b, c, d)

где a, b – нижний и верхний пределы внутреннего интеграла; c, d – нижний и верхний пределы наружного интеграла.

Также имеется возможность вычислять интегралы с переменным верхним пределом. Вычисление такого интеграла производится теми же функциями, что обычные определенные интегралы. Для нахождения такого интеграла пишутся две функции: для подынтегральной функции и находящую значения интеграла для каждого значения переменного верхнего предела (это число является входной переменной данной функции).

6.5 Интерполирование

Табличные данные очень часто удобно интерпретировать как некоторую функцию, в частности сплайн (полиномиальную) (рис. 6.4). Если возникает задача о построении полиномиальной или кусоч- но-полиномиальной функции для приближения некоторых исходных данных, то существуют в MatLab

встроенные функции для приближения сплайнами как одномерных, так и многомерных данных. Некоторые встроенные функции интерполирования в MatLab приведены в табл. 10.

10 Функции MatLab для интерполяции табличных данных

Более подробно об интерполировании таблично заданных функций можно узнать из справочной системе MatLab.

Пример: Интерполяция таблично заданных функций.

%задание табличной функции x = [0.1 0.2 0.4 0.5 0.6 0.8 1.2]; y = [-3.5 -4.8 -2.1 0.2 0.9 2.3 3.7];

%задание промежуточных точек для интерполирования xi = [x(1):0.01:x(length(x))];

ynear = interp1(x, y, xi, 'nearest'); yline = interp1(x, y, xi, 'linear'); yspline = interp1(x, y, xi, 'spline');

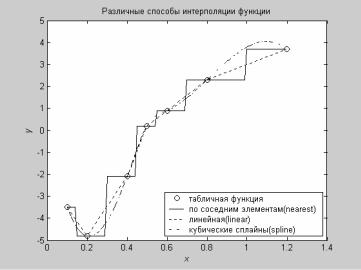
Рис. 6.4 Различные способы интерполяции функции одной переменной

6.6Оптимизация

Всостав MatLab входят функции, предназначенные для решения линейных и нелинейных, безусловных и условных оптимизационных задач. Основные функции оптимизации приведены в табл. 11.

11 Основные функции MatLab для решения задач оптимизации

tions,P1,P2)

1Безусловная минимизация функций. Минимизация функции одной переменной производится

спомощью команды fminbnd. Данная команда определяет локальный минимум в точке, близкой к точке приближения. Использование этой команды аналогично использованию команды fzero.

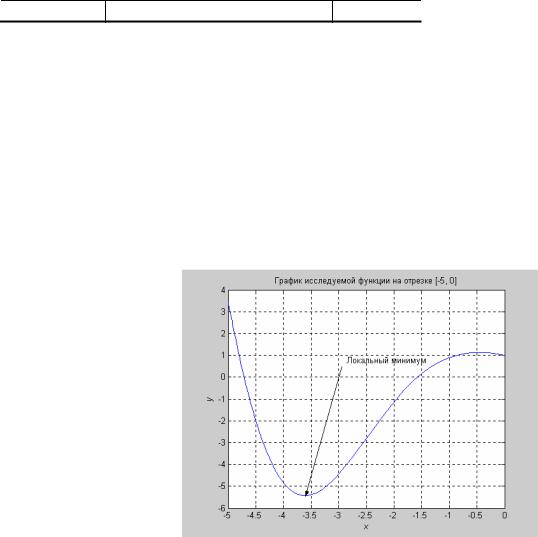
Пример: Найти локальный минимум уравнения sinx−x2 cos(x)=0 на отрезке [–5, 0]. Исследуемая функция сохраняется в файл-функции 'myf', график исследуемой функции представлен на рис. 6.5.

>> x = fminbnd('myf', -5, 0)

x=

-3.6052

Рис. 6.5 Иллюстрация к примеру

Если необходимо найти безусловный минимум функции нескольких переменных, то используется команда fminsearch. перед применением fminsearch необходимо создать файл-функцию, вычисляющую значения искомой функции, причем аргументом данной функции должен быть вектор, элементы которого являются аргументами минимизируемой функции.

Пример. Определить локальный минимум функции

Сначала исследуем поведение данной функции для определения хорошего начального приближения. Для этого построим линии равного уровня исследуемой функции (рис. 6.6).

Файл-функция для оптимизации: function f = ftest(arg)

x = arg(1); y = arg(2);

f = sin(pi*x).*sin(pi*y);

Зная начальное приближение (определяется из графика на рис. 6.6), можно вызвать функцию fminsearch (указывая вектор начального приближения).

>> M = fminsearch('ftest', [1.4, 0.6])

M =

1.5000 0.5000