ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

59. Уравнение Эйлера

Опр2. Уравнения вида

(10)

где все - постоянные, называютсяуравнениями Эйлера. Уравнение Эйлера заменой независимого переменного (или, еслих<0; в дальнейшем для определенности будем считать х>0 ) преобразуется в линейное однородное уравнение с постоянными коэффициентами.

Действительно, линейность и однородность уравнения при преобразовании независимого переменного сохраняются, а коэффициенты становятся постоянными, потому что

(11)

где все - постоянные, и при подстановке в уравнение (10) множителисокращаются с множителями.

Справедливость равенства (11) легко может быть доказана методом индукции.

Действительно, допустив, что равенство (11) справедливо, и продифференцировав его еще раз по х, докажем справедливость равенства (11) и для :

где все - постоянные.

Итак, справедливость формулы (11) доказана, и следовательно, линейно входящие в уравнение Эйлера

(10`)

с постоянными коэффициентами произведения

Линейно выражаются через производные функции y по новой независимой переменной t. Отсюда следует, что преобразованное уравнение будет линейным однородным уравнением с постоянными коэффициентами

. (12)

Вместо того чтобы преобразовывать уравнение Эйлера в линейное уравнение с постоянными коэффициентами, частные решения которого имеют вид , можно сразу же искать решения исходного уравнения в виде, так как

.

Получающееся при этом после сокращения на уравнение

(13)

для определения k должно совпадать с характеристическим уравнением для преобразованного уравнения (12). Следовательно, корням уравнения (13) кратностисоответствуют решения

, ,,…,

преобразованного уравнения или

исходного уравнения, а комплексным сопряженным корням уравнения (13) кратностисоответствуют решения

преобразованного уравнения или

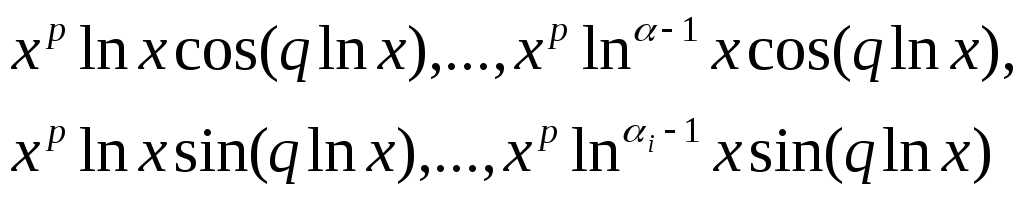
исходного уравнения Эйлера.

Уравнения вида

(14)

также называются уравнениями Эйлера и сводятся к уравнению (10) заменой независимого переменного или преобразовать уравнение (14) к линейному однородному уравнению с постоянными коэффициентами заменой переменных(или, еслиax+b<0 ).

57. Линейное уравнение n-го порядка с постоянными коэффициентами. Метод вариации произвольных постоянных.

Линейные неоднородные уравнения

Линейное неоднородное уравнение с постоянными коэф. имеет вид

.

При решении линейных неоднородных уравнений с постоянными коэффициентами во многих случаях без труда удается подобрать частные решения и тем самым свести задачу к интегрированию соответствующего однородного уравнения.

Пусть, например, правая часть является многочленом степени s, и, следовательно, уравнение имеет вид

(15)

где все и- постоянные.

Если , то существует частное решение уравнения (15), имеющее тоже вид многочлена степениs. Действительно, подставляя

в уравнение (15) и сравнивая коэффициенты при одинаковых степенях x в левой м правой частях, получаем для определения коэффициентов всегда разрешимую, если, систему линейных уравнений:

откуда определяется ,

откуда определяется ,

откуда определяется .

Итак, если , то существует частное решение, имеющее вид многочлена, степень которого равна степени многочлена, стоящего в правой части.

Предположим теперь, что , причем для общности допустим, что и, но, т.е.k=0 не является α-кратным корнем характеристического уравнения, причем случай α=1 не исключается. При этом уравнение (15) принимает вид

(16)

Полагая , мы приходим к предыдущему случаю, и, следовательно существует частное решение уравнения (16), для которого

а значит, у является многочленом степени s + α, причем члены, начиная со степени α -1 и ниже, у этого многочлена будут иметь произвольные постоянные коэффициенты, которые могут быть, в частности, выбраны равными нулю. Тогда частное решение примет вид:

Рассмотрим теперь линейное неоднородное уравнение вида

(17)

где все и- постоянные. Замена переменныхпреобразует ур. (17) к виду:

,или

, (18)

где - постоянные.

Частное решение уравнения (18), если , имеет вид

а значит , частное решение ур.(17)

Условие означает, чтоне является корнем характеристического уравнения

(19)

а следовательно, k=р не является корнем характеристического уравнения

(20)

так как корни этих характеристических уравнений связаны зависимостью .

Если же является корнем характеристического уравнения (19) кратности α, другими словами,k=р является корнем характеристического уравнения (20) той же кратности α, то частные решения уравнений (18) и (17) имеют соответственно вид

Итак, если правая часть линейного дифференциального уравнения с постоянными коэффициентами имеет вид

,

то, если р не является корнем характеристического ур-я, частное решение надо искать в таком же виде:

.

Если же р является корнем характеристического уравнения кратности α (этот случай называется особым или резонансным ), то частное решение надо искать в виде

Эти рассуждения остаются справедливыми и при комплексном р, поэтому если правая часть линейного диф.ур-я имеет вид

(21)

где один из многочленов илиимеет степеньs, а другой – степень не выше чем s,то, преобразуя тригонометрические функции по формулам Эйлера к показательному виду, получим в правой части

(22)

где и- многочлены степениs.

Для каждого слагаемого правой части можно уже применить указанное выше правило, а именно, если не являются корнями характеристического уравнения, то частное решение можно искать в таком же виде, как и правая часть (22); если жеявляются корнями характеристического уравнения кратности α, то частное решение приобретает еще множитель.

Если опять вернуться к тригонометрическим функциям, то это правило можно сформулировать так:

а) Если не являются корнями характеристического уравнения, то частное решение надо искать в виде

,

где и -многочлены степени s с неопределенными коэффициентами.

Заметим, что если один из многочленов илиимеет степень нижеs или даже, в частности, тождественно равен нулю, то все же оба многочлена ибудут, вообще говоря, имеет степеньs.

б) Если являются α-кратными корнями характеристического уравнения (резонансный случай), то частное решение надо искать в виде

.

28. 28.Рассмотрим систему вида Y′-AY=eP(x) (5), Систему лин.диф.уравнений будем называть неоднородной системой (5).

По аналогии с лин. Уравнениями можно показать, что общ.решение системы (5) есть сумма общего решения однород.уравнения (2) и некоторого частного решения системы (5).

Рассмотрим случай, когда все собств.значения матрицы А простые (различные).

Задача: Научится определять част.решения для системы (5). Рассмотрим 2 случая:

1.Пусть μ – не является собст.значением матрицы А (нерезонансный случай )

- вектор многочленов (6)

, где pj- постоян.вектор, . Подставим (6) в (5)

=

и т.д.

(7)

Т.о.Qm мы определили, где все коэффициенты вычисляются по формуле (7)

2.Пусть μ является собст.значением матрицы А (резонансный).

и λ1… λn – собств.значения А,

Существует матрица T:Λ=diag{λi}. Сделаем замену переменных в формуле (5) , умножим на

(8). Расписывая уравнение (8) получим след вид

(9)

Где , j=1,n, pij – const € R

Все уравнения системы (9) являются лин.диф.уравнениями 1-го порядка с правой частью квазимногочленов. к-е уравнения являются случаем резонанса, а все остальные – нерезонансные (т.к. ). Для к-го уравнения част.решение будем искать в виде.

(10)

Объединяя (10) в единое целое получим, что , где- вектор многочленов степениm+1

. Т.о. мы доказали следующее утверждение.

Утверждение 1.Если в уравнении (5) μ – является собст.значением матрицы А, тогда част.решение уравнения (5) необходимо искать в виде

Утверждение 2. Если в уравнении (5) μ не является собств.значением матрицы А, то част.решение (5) необходимо искать в виде

Случай кратных корней.

1. существует T:

2). Cуществует , Ji имеет размерность ki

Рассмотрим простой случай ,- собств.вектор матрицыJ, соответствующий собст.значению λ.

J

→x2=x3=x4=…=xk=0, x1=1 →

-собств.вектора для матрицы J

. Тогда

Опр. Если система векторов f1…fk удовлетворяют равенствам Af1=λf1, Af2=λf2+f1….Afk=λfk+fk-1. тогда говорят, что система векторов определяет жорданову цепочку. f1..fk называют присоединенными векторами к вектору f1. f1 является собств.вектором матрицы А, соответствующий собст.значению λ. к – длина жордановой цепочки . Ji называют жордановыми клетками.

Рассмотрим уравнение вида.

, где

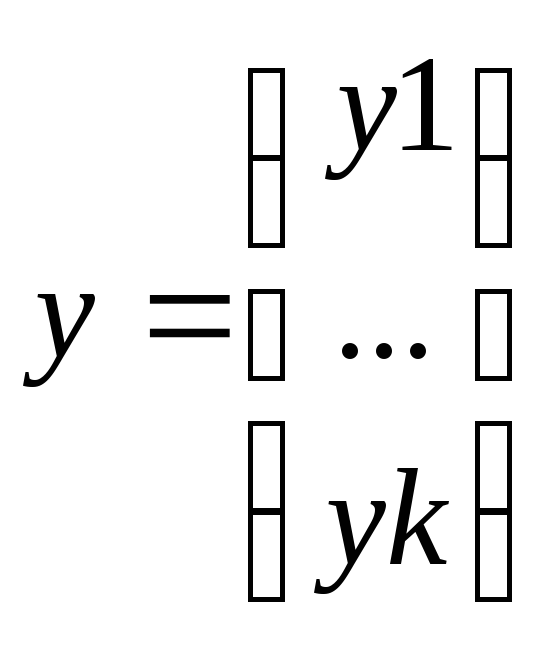
Рассмотрим уравнение вида где

Предположим, что матрица А имеет собств.значения λ1… λs кратности k1…ks соответственно. Тогда существует сделаем замену переменной

. Последнее уравнение запишем в следующем виде

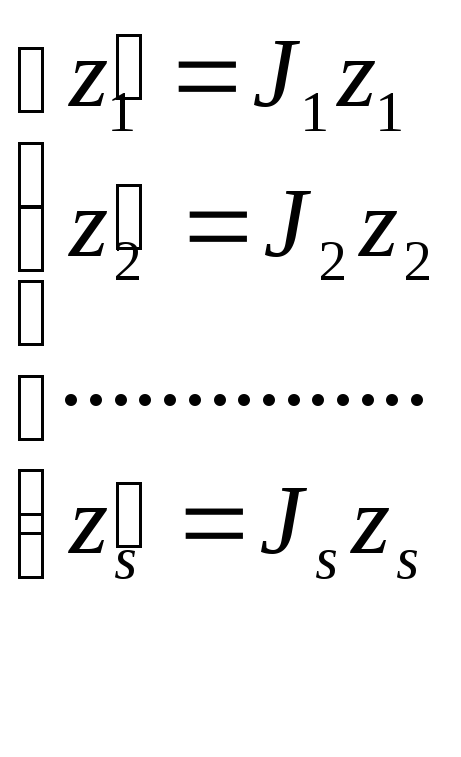, где zi – вектора, имеющие размерность ki

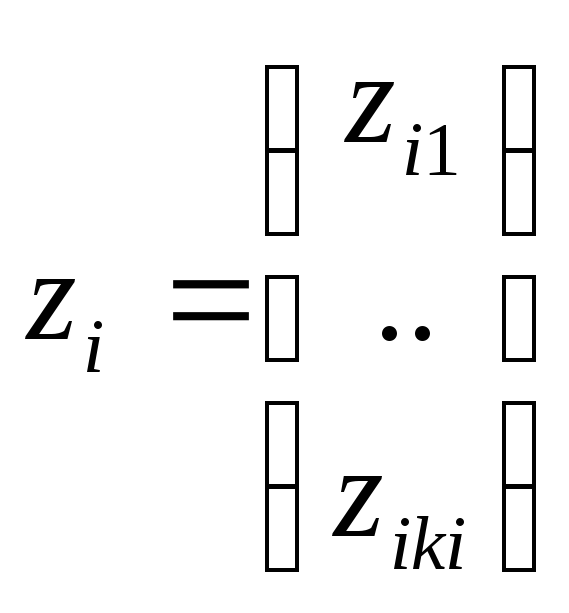и каждый блок решаем по отдельности.

=Общее решение