Системы дифференциальных уравнений

(1)

Система такого вида называется нормальной системой дифференциальных уравнений (СНДУ). Для нормальной системы дифференциальных уравнений можно сформулировать теорему о существовании и единственности такую же, как и для дифференциального уравнения.

Теорема. Если функции определены и непрерывны на открытом множестве, а соответствующие частные производныетоже непрерывны на, то тогда у системы (1) будет существовать решение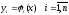(2)

а при наличии начальных условий (3)

это решение будет единственным.

Эту систему можно представить в виде:

(4)

Системы линейных дифференциальных уравнений

Определение. Система Дифференциальных Уравнений называется линейной, если она линейна относительно всех неизвестных функций и их производных.

(5)

Общий вид системы Дифференциальных Уравнений

(6)

Если задано начальное условие: , (7)

то решение будет единственным, при условии, что вектор-функция непрерывна наи коэффициенты матрицы:тоже непрерывные функции.

Введем линейный оператор , тогда (6) можно переписать в виде:

, (8)

если то операторное уравнение (8) называетсяоднородным и имеет вид:

. (9)

Так как оператор линейный, то для него выполняются следующие свойства:

1. Если решение однородной системы (9), тобудет тоже

решением уравнения (9).

2. Если являются решением (9), тотоже решение (9).

Следствие. Линейная комбинация , решение (9).

Если даны решений (9) и они линейно независимы, то все линейные комбинации вида: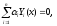(10) только при условии, что все. Это означает, что определитель, составленный из решений (10):

. Этот определитель называется определителем Вронского для системы векторов .

Теорема 1. Если определитель Вронского для линейной однородной системы (9) с непрерывными на отрезке коэффициентами, равен нулю хотя бы в одной точке, то решениелинейно зависимы на этом отрезке и, следовательно, определитель Вронского равен нулю на всем отрезке.

Доказательство: Так как непрерывны, то система (9) удовлетворяет условиюТеоремы о существовании и единственности, следовательно, начальное условие определяет единственное решение системы (9). Определитель Вронского в точкеравен нулю, следовательно, существует такая нетривиальная система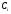, для которой выполняется:. Соответствующая линейная комбинация для другой точкибудет иметь вид, причемудовлетворяет однородным начальным условиям, следовательно, совпадает с тривиальным решением, то естьлинейно зависимы и определитель Вронского равен нулю.

Определение. Совокупность решений системы (9) называетсяфундаментальной системой решений на если определитель Вронского не обращается в ноль ни в одной точке.

Определение. Если для однородной системы (9) начальные условия определены следующим образом - , то система решенийназываетсянормальной фундаментальной системой решений.

Замечание. Если 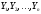- фундаментальная система или нормальная фундаментальная система, то линейная комбинация- общее решение (9).

Теорема 2. Линейная комбинация линейно независимых решений,однородной системы (9) с непрерывными на отрезкекоэффициентамибудет общим решением (9) на этом же отрезке.

Доказательство: Так как коэффициенты непрерывны на, то система удовлетворяет условиям теоремы о существовании и единственности. Следовательно, для доказательства теоремы достаточно показать, что подбором постоянных, можно удовлетворить некоторому произвольно выбранному начальному условию (7). Т.е. можно удовлетворить векторному уравнению:. 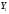Так как- общее решение (9), то система разрешима относительно, поскольку вселинейно независимы и. Однозначно определяем, а так каклинейно независимы, то.

Теорема 3. Если это решение системы (8), арешение системы (9), тогда+будет тоже решение (8).

Доказательство: По свойствам линейного оператора: 

Теорема 4. Общее решение (8) на отрезке с непрерывными на этом отрезке коэффициентами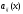и правыми частямиравно сумме общего решения соответствующей однородной системы (9) и частного решениянеоднородной системы (8).

Доказательство: Так как условия теоремы о существовании и единственности выполнены, следовательно, остается доказать, что будет удовлетворять произвольно заданным начальным значением (7), то есть. (11)

Для системы (11) всегда можно определить значения . Это можно сделать так как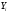- фундаментальная система решений.

Задача Коши для дифференциального уравнения первого порядка

Постановка задачи. Напомним, что решением обыкновенного дифференциального уравнения первого порядка

y'(t)=f(t, y(t)) (5.1)

называется дифференцируемая функция у(t), которая при подстановке в уравнение (5.1) обращает его в тождество. График решения дифференциального уравнения называют интегральной кривой. Процесс нахождения решений дифференциального уравнения принято называть интегрированием этого уравнения.

Исходя из геометрического смысла производной у' заметим, что уравнение (5.1) задает в каждой точке (t, у) плоскости переменных t, у значение f(t, у) тангенса угла aнаклона (к оси 0t) касательной к графику решения, проходящего через эту точку. Величину k=tga=f(t,у) далее будем называть угловым коэффициентом (рис. 5.1). Если теперь в каждой точке (t, у) задать с помощью некоторого вектора направление касательной, определяемое значением f(t, у), то получится так называемое поле направлений (рис.5.2, а). Таким образом, геометрически задачу интегрирования дифференциальных уравнений состоит в нахождении интегральных кривых, которые в каждой своей точке имеют заданное направление касательной (рис. 5.2, б). Для того, чтобы выделить из семейства решений дифференциального уравнения (5.1) одно конкретное решение, задают начальное условие

y(t₀)=y₀ (5.2)

Здесь t₀ — некоторое фиксированное значение аргумента t, а у₀ величина, называемая начальным значением. Геометрическая интерпретация использования начального условия состоит в выборе из семейства интегральных кривых той кривой, которая проходит через фиксированную точку (t₀, у₀).

Задачу нахождения при t>t₀ решения у(t) дифференциального уравнения (5.1), удовлетворяющего начальному условию (5.2), будем называть задачей Коши. В некоторых случаях представляет интерес поведение решения при всех t>t₀. Однако чаще ограничиваются определением решения на конечном отрезке [t₀,T].

Интегрирование нормальных систем

одним из основных методов интегрирования нормальной системы ДУ является метод сведения системы к одному ДУ высшего порядка. (Обратная задача - переход от ДУ к системе - рассмотрена выше на примере.) Техника этого метода основана на следующих соображениях.

Пусть задана нормальная система (6.1). Продифференцируем по х любое, например первое, уравнение:

Подставив в это равенство значения производных из системы (6.1), получим

или, коротко, 

Продифференцировав полученное равенство еще раз и заменив значения производных из системы (6.1), получим

Продолжая этот процесс (дифференцируем - подставляем - получаем), находим:

Соберем полученные уравнения в систему:

Из первых (n-1) уравнений системы (6.3) выразим функции у₂, у₃, ..., y_n через х, функцию y₁ и ее производные у'₁,у"₁,...,у₁^(n-1). Получим:

Найденные значения у₂, у₃,..., у_n подставим в последнее уравнение системы (6.3). Получим одно ДУ n-го порядка относительно искомой функции   Пусть его общее решение есть

Продифференцировав его (n-1) раз и подставив значения производных в уравнения системы (6.4), найдем функции у₂, у₃,..., у_n.

 

Пример 6.1. Решить систему уравнений

Решение: Продифференцируем первое уравнение: у"=4у'-3z'. Подставляем z'=2у-3z в полученное равенство: у"=4у'-3(2у-3z), у"-4у'+6у=9z. Составляем систему уравнений:

Из первого уравнения системы выражаем z через у и у':

Подставляем значение z во второе уравнение последней системы:

т. е. у''-у'-6у=0. Получили одно ЛОДУ второго порядка. Решаем его: k²-k-6=0, k₁=-2, k₂=3 и - общее решение

уравнения. Находим функцию z. Значения у и подставляем в выражение z через у и у' (формула (6.5)). Получим:

Таким  образом, общее решение данной системы уравнений имеет вид

Замечание. Систему уравнений (6.1) можно решать методом интегрируемых комбинаций. Суть метода состоит в том, что посредством арифметических операций из уравнений данной системы образуют так называемые интегрируемые комбинации, т. е. легко интегрируемые уравнения относительно новой неизвестной функции.

Проиллюстрируем технику этого метода на следующем примере.

Пример 6.2. Решить систему уравнений:

Решение: Сложим почленно данные уравнения: х'+у'=х+у+2, или (х+у)'=(х+у)+2. Обозначим х+у=z. Тогда имеем z'=z+2. Решаемполученное уравнение:

Получили так называемый первый интеграл системы. Из него можно выразить одну из искомых функций через другую, тем самым уменьшить на единицу число искомых функций. Например,Тогда первое уравнение системы примет вид

 

Найдя из него х (например, с помощью подстановки х=uv), найдем и у.

 

Замечание. Данная система «позволяет» образовать еще одну интегрируемую комбинацию:  Положив х - у=р, имеем:, или Имея два первых интеграла системы, т. е.и легко найти (складывая и вычитая первые интегралы), что 

59. Линейный оператор, свойства. Линейная зависимость и независимость векторов. Определитель Вронского для системы ЛДУ.

Линейный дифференциальный оператор и его свойства. Множество функций, имеющих на интервале (a, b) не менее n производных, образует линейное пространство. Рассмотрим оператор L_n(y), который отображает функцию y(x), имеющую производных, в функцию, имеющуюk - n производных:

(23)

С помощью оператора L_n(y) неоднородное уравнение (20) можно записать так:

Ln(y) = f(x);

(24)

однородное уравнение (21) примет вид

Ln(y) = 0);

(25)

Теорема 14.5.2. Дифференциальный оператор L_n(y) является линейным оператором.  Док-во непосредственно следует из свойств производных:  1. ЕслиC = const, то 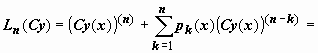2.Наши дальнейшие действия: сначала изучить, как устроено общее решение линейного однородного уравнения (25), затем неоднородного уравнения (24), и потом научиться решать эти уравнения. Начнём с понятий линейной зависимости и независимости функций на интервале и определим важнейший в теории линейных уравнений и систем объект - определитель Вронского.

 Определитель Вронского. Линейная зависимость и независимость системы функций.  Опр. 14.5.3.1.Система функций y₁(x), y₂(x), …, y_n(x) называется линейно зависимой на интервале (a, b), если существует набор постоянных коэффициентов , не равных нулю одновременно, таких, что линейная комбинация этих функций тождественно равна нулю на (a, b): для.Если равенстводлявозможно только при, система функцийy₁(x), y₂(x), …, y_n(x) называется линейно независимойна интервале (a, b).  Другими словами, функцииy₁(x), y₂(x), …, y_n(x) линейно зависимы на интервале (a, b), если существует равная нулю на (a, b) их нетривиальная линейная комбинация. Функции y₁(x),y₂(x), …, y_n(x) линейно независимы на интервале (a, b), если только тривиальная их линейная комбинация тождественно равна нулю на (a, b).  Примеры: 1. Функции 1,x, x², x³ линейно независимы на любом интервале (a, b). Их линейная комбинация - многочлен степени- не может иметь на (a, b)больше трёх корней, поэтому равенство = 0 длявозможно только при.Пример 1 легко обобщается на систему функций 1,x, x², x³ , …, xⁿ. Их линейная комбинация - многочлен степени - не может иметь на (a, b) больше n корней.  3. Функциилинейно независимы на любом интервале (a, b), если . Действительно, если, например,, то равенствоимеет место в единственной точке.4. Система функцийтакже линейно независима, если числаk_i (i = 1, 2, …, n) попарно различны, однако прямое доказательство этого факта достаточно громоздко.  Как показывают приведённые примеры, в некоторых случаях линейная зависимость или независимость функций доказывается просто, в других случаях это доказательство сложнее. Поэтому необходим простой универсальный инструмент, дающий ответ на вопрос о линейной зависимости функций. Такой инструмент -определитель Вронского.

Опр. 14.5.3.2. Определителем Вронского (вронскианом) системы n - 1 раз дифференцируемых функций y₁(x), y₂(x), …, y_n(x) называется определитель

.

(26)

14.5.3.3.Теорема о вронскиане линейно зависимой системы функций. Если система функций y₁(x), y₂(x), …, y_n(x) линейно зависима на интервале (a, b), то вронскиан этой системы тождественно равен нулю на этом интервале.  Док-во. Если функции y₁(x), y₂(x), …, y_n(x) линейно зависимы на интервале (a, b), то найдутся числа , из которых хотя бы одно отлично от нуля, такие что

для .

(27)

Продифференцируем по x равенство (27) n - 1 раз и составим систему уравнений Будем рассматривать эту систему как однородную линейную систему алгебраических уравнений относительно. Определитель этой системы - определитель Вронского (26). Приэта система имеет нетривиальное решение, следовательно, в каждой точке её определитель равен нулю. Итак,W(x) = 0 при , т.е.на (a, b).