55

Уравнение Я. Бернулли

Уравнение вида

(48.15)

называется уравнением Бернулли. Покажем, что его можно привести к линейному.

Если , то ДУ (48.15) — линейное, а при n = 1 — с разделяю­щимися переменными.

В общем случае, разделив уравнение (48.15) на , получим:

(48.16)

Обозначим 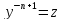Тогда Отсюда находим

Уравнение (48.16) принимает вид

Последнее уравнение является линейным относительно Решение его известно. Таким образом, подстановка сводит уравнение (48.15) к линейному. На практике ДУ (48.15) удобнее искать методом И. Бернулли в виде(не сводя его к линейному).

Уравнение в полных дифференциалах. Интегрирующий множитель

Уравнение

(48.17)

называется уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой функции , т. е.

В этом случае ДУ (48.17) можно записать в виде , а его общий интеграл будет:

(48.18)

Приведем условие, по которому можно судить, что выражение

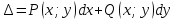
есть полный дифференциал.

Теорема 48.2. Для того чтобы выражение

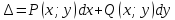
где функции и их частные производные

непрерывны в некоторой области D плоскости Оху, было полным дифференциалом, необходимо и достаточно выполнение условия

(48.19)

Необходимость

Пусть есть полный дифференциал, т. е.

Учитывая, что (см. п. 44.3), имеем:

Дифференцируя эти равенства по у и по x соответственно, получаем

А так как смешанные частные производные

равны между собой (см. п. 44.2), получаем (48.19).

Достаточность

Пусть в области D выполняется условие (48.19). Покажем, что су­ществует функция u(х; у) в области D такая, что

Найдем эту функцию. Искомая функция должна удовлетворять требо­ваниям:

(48.20)

Если в первом уравнении (48.20) зафиксировать у и проинтегриро­вать его по х, то получим:

(48.21)

Здесь произвольная постоянная зависит от у (либо является числом). В решении (48.21) не известна лишь. Для ее нахождения продифференцируем функщпо (48.21) по у:

Используя второе равенство (48.20), можно записать:

Отсюда

(48.22)

В равенстве (48.22) левая часть зависит от y. Покажем, что и правая часть равенства зависит только от y.

Для этого продифференцируем правую часть по х и убедимся, что производная равна нулю. Действительно,

в силу условия (48.19).

Из равенства (48.22) находим

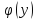
Подставляя найденное значение дляв равенство (48.21), находим функциютакую, что■

Таким образом, при решении ДУ вида (48.17) сначала проверяем выполнение условия (48.19). Затем, используя равенства (48.20), находим функцию u(х;у). Решение записываем в виде (48.18).

Если условие (48.19) не выполняется, то ДУ (48.17) не является уравнением в полных дифференциалах.

Однако это уравнение иногда можно привести к уравнению в пол- пых дифференциалах умножением его на некоторую функцию t(x;у), называемую интегрирующим множителем.

Чтобы уравнение t(x;у) * Р(х; у) dx + t(x; у) * Q(x;y) dy = 0 было уравнением в полных дифференциалах, должно выполняться условие

Выполнив дифференцирование

и приведя подобные слагаемые, получим

(48.23)

Для нахождения t(x; у) надо проинтегрировать полученное ДУ в частных производных. Решение этой задачи не простое. Нахождение интегрирующего множителя может быть упрощено, если допустить су­ществование t как функции только одного аргумента х либо только у. Пусть, например, t = t(x). Тогда уравнение (48.23) принимает вид

или

Отсюда (48.24)

При этом выражение должно зависеть только от х.

Аналогично получаем, что если t = t(y) (t не зависит от x), то

а подынтегральное выражение должно зависеть только от у.

56 Задача коши для оду

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Основные понятия

Дифференциальное уравнение первого порядка в общем случае можно записать в виде

F(x,y,y') = 0. (48.1)

Уравнение связывает независимую переменную x, искомую функции» у и ее производную у'. Если уравнение (48.1) можно разрешить огни сительно у’ то его записывают в виде

у' = f(x; у) (48.2)

и называют ДУ первого порядка, разрешенным относительно производной. Мы в основном будем рассматривать эту форму записи ДУ.

Уравнение (48.2) устанавливает связь (зависимость) между координатами точки (х; у) и угловым коэффициентом у' касательной к интегральной кривой, проходящей через эту точку. Следовательно ДУ у' = f(x;y) дает совокупность направлений (поле направлений) на плоскости Оху. Таково геометрическое истолкование ДУ первого порядка.

Кривая, во всех точках которой направление поля одинаково, называется изоклиной. Изоклинами можно пользоваться для приближенного построения интегральных кривых. Уравнение изоклины можно по­лучить, если положить у' = с, т. е. f(x; у) = с.

Дифференциальное уравнение первого порядка, разрешенное от­носительно производной, можно записать в дифференциальной форме:

Р(х; у) dх + Q(x; у) dy = 0, (48.3)

Р(х; у) и Q(x;y) — известные функции. Уравнение (48.3) удобно мм, что переменные х и у в нем равноправны, т. е. любую из них можнo рассматривать как функцию другой. Отметим, что от одного вида записи ДУ можно перейти к другому.

Интегрирование ДУ в общем случае приводит к бесконечному множеству решений (отличающихся друг от друга постоянными величи­нами). Легко догадаться, что решением уравнения у’ = х является Функция , а также,и вообще, где с — const.

Чтобы решение ДУ приобрело конкретный смысл, его надо подчи­нить некоторым дополнительным условиям.

Условие, что при функция у должна быть равна заданному числут. е.называетсяначальным условием. Начальное условие записывается в виде

(48.4)

Общим решением ДУ первого порядка называется функция , содержавшая одну произвольную постоянную и удовлеворяющая условиям:

1. Функция является решением ДУ при каждом фиксированном значении с.

2. Каково бы ни было начальное условие (48.4), можно найти такое значение постоянной , что функцияудовлетворяет данному начальному условию.

Частным решением ДУ первого порядка называется любая функция , полученная из общего решенияпри конкретном значении постоянной.

Если общее решение ДУ найдено в неявном виде, т. е. в виде урав­нения , то такое решение называетсяобщим интегралом ДУ. Уравнение в этом случае называется частным ин­тегралом уравнения.

С геометрической точки зрения есть семейство инте­гральных кривых на плоскости Оху; частное решение— одна кривая из этого семейства, проходящая через точку

Задача отыскания решения ДУ первого порядка (48.3), удовлетво­ряющего заданному начальному условию (48.4), называется зада­чей Коши.

Теорема 48.1 (существования и единственности решения задачи Коши). Если в уравнении (48.2) функцияи ее частная про­изводнаянепрерывны в некоторой области D, содержащей точку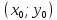то существует единственное решение уэтого уравнения, удовлетворяющее начальному условию (48.4).

(Без доказательства).

Геометрический смысл теоремы состоит в том, что при выполнении ее условий существует единственная интегральная кривая ДУ, проходящая через точку

Рассмотрим теперь методы интегрирования ДУ первого порядка определенного типа.

1. Обыкновенные дифференциаьные уравнения первого порядка. Уравнения с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка.

Уравнение в которых неизвестная функция содержится в виде дифференциала или производной называется Д.У.

Если к д.у функция зависит только от одной переменной, то д.у называетсяобыкновенной. Если функция зависит от двух и более переменных, то уравнение называетсяд.у в частных производных.

Порядком д.у. называется наивысшей порядок произвольной, присутствующий в данном уравнении.

Решая любое д.у. неизвестную функцию. Решением д.у. называется функция при подстановке которой в данное уравнение получается верное равенство.

Обыкновенные Д.У. первого порядка.

Д.У. первого порядка называется уравнение связывающее независимо переменную неизвестную функциюи первую производную от функции.

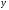Если в таком уравнении производную функцию можно выразить через и, то уравнение называетсяразрешенным относительно производных.

(1)

В уравнении (1) правая часть может рассматриваться как некоторая функция двух переменных . Рассмотрим геометрический смысл уравнения (1).

Т.к. в левой части уравнения (1) находится производная функции , а производная геометрически представляет собой уголовной коэффициент графика функции, то уравнение (1) составит в соответствии в каждой точке, координаты плоскости некоторый коэффициент касательной. По-другому Д.У. (1) задает поле напрвалении вдоль интегральных кривых.

Геометрические решения уравнения (1) означает нахождение семейства интегральных кривых отличающему заданному полю.

Т.о., задачи интегрирования Д.У. геометрически заключаются в том, чтоы найти кривые в каждой точке, которых напрвление касательных совпадает с полем направления.

Пример 1.

или

В данном уравнении каждой точке в координатной плоскости ставится соответствие угловой коэффициент касательной. Геометрически данное уравнение определяется к след. полю направления.

Действительно рассматриваемое поле направления определяют интегральные кривые в виде прямых проходящие через начало координат.

- решение данного Д.У. где -.

Проверка: ;.

и в данное уравнение,.

Пример 2.

или

В данное уравнение в каждой точке 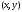в координатной плоскости ставит в соответствии угловой коэффициентПричем, этот угловой коэффициент ортогонален угловому коэффициенту предыдущему уравнению, т.к.Поэтому поле направлений в каждой точкебудет перпендикулярна предыдущему уравнению.

Видно, что такое поле напраление задает концентрические окружности с одним и теми же координатами. В начале координаты интегральные кривые окружности.

- решение Д.У. неявное.

Кривая в каждой точке в которой поле направления одинакова называетсяизоклинами. Изоклины удобно использовать при построении поля направлений. Уравнение изоклин получается из равенства .

Пример 3.

С помощью изоклин определить вид интегральных кривых для уравнения .

Найдем уравнения изоклин.

; =>- изоклины, прямые перпендикулярные к оси.

Для каждой изоклины найдем поле направлеия.

При .

При .

При .

При .

При .

Такое поле направление определяет интегральные кривые в виде перабол. Действительно, уравнение имеет вид: .

Уравнение с разделяющими переменными.

Уравнение вида: , где

- непрерывные функции в своих облостях называется уравнения с разделяющими переменными.

Интегрируем обе части полученного уравнения

(1)

Из последнего уравнения находим функцию или функцию. Уавнение с разделяющимися переменнымииявляется равноправными переменными.

Замечание.

При разделении переменных может производиться деление на функцию, при этом считается, что функция не равна 0, . Поэтому необходимо проверить является ли корень(2) корнем исходного уравнения. Т.о., уравнение с разделяющимися переменными решения имеет вид решение уравнения (1) и решение уравнения (2).

Замечание.

К уравнениям с разделяющими переменными сводится уравнение вида: , где- некоторые числа.

Сделаем замену:

; .

Подставим и заменув первоначальное уравнение.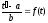

Поучившееся уравнение относительно иможно рассмотреть как уравнение с разделяющимися переменными.

; ;;.

Из последнего равенства можно выразить черезиличерези далее возвращаемся к замене переменной.

Однородные Д.У. первого порядка.

Определение: однородным Д.У первого порядка называется уравнение вида: , где- непрерывная функция.

Понятие однородного Д.У. связано понятие с однородной функцией.

Функция 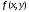называетсяоднородной в 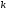-ой степени, если выполняется равенство:, где.

Выяснить являются ли однородными след. функции:

1. .

- функция однородная 2-ой степени.

2. 

- однородная функция в 0-ой степени.

3. 

- не является однородной функцией.

Рассмотрим еще одно определение однородного Д.У. первого порядка.

Уравнение вида , где- однородная функция 0-ого порядка называетсяоднородным Д.У. первого порядка.

Рассмотрим метод решения однородного Д.У. первого порядка.

Введем замену: ;. Подставляя замену в исходное уравнение, получим:.

Полученное уравнение можно рассмотреть как уравнение с разделяющими переменными:

; .

Т.о., однородное Д.У. с помощью замены сводится к уравнению с разделяющими переменными.