Связь между матрицами линейного оператора в различных базисах.

Рассмотрим А:L→ L΄.

Пусть е1,…,еn – базис в L, h1,…,hm- базис в L´.

Нашему линейному оператору А(х) соответствует матрица А: А(х)=Ах

Тогда следует ожидать, что при замене базиса матрица А меняется.

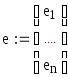базис в L, базис в L´

Пусть новый базис в L.S – матрица перехода от старого базиса к новому, т.е.

Пусть новый базис в L´

Р – матрица перехода .

Тогда для любого х €L А(х)=Ах=у €L´,где ,Пустькоординаты х в новом базисе,координаты у в новом базисе

Следовательно, х=Sx´, y=Py´

А Sx´=Ру´, .

С другой стороны мы ищем матрицу А´: А´х´=у´. Следовательно, - закон изменения матрицы А при переходе к новому базису или иначе, связь между матрицами.

Собственные вектора и собственные числа.

Опр1.Ненулевой вектор х в L называют собственным вектором линейного оператора А:L→ L, если для некоторого действительного числа λ выполняется соотношение Ах= λх. При этом число λ называют собственным значением (собственным числом) линейного оператора А.

Ах=λх=λЕх,

=

, отсуда (А-λЕ)х=0

Собственный вектор х находится из однородной системы уравнений . Собственные вектора существуют, если det(A-λE)=0. Это уравнение называется характеристическим уравнением оператора А(х), заданного матрицей А в базисе е1,…,en.

Утверждение. Характеристическое уравнение не зависит от выбора базиса.

◄ пусть е´ новый базис. S матрица перехода от базиса е к е´. Тогда , где А´ - матрица оператора А(х) в базисе е´

det(A-λE)= = ==det *det(A-λE)*detS= det(A-λS)►

Определение. Собственные числа – решение характеристического уравнения det(A-λE)=0

det Известно, что определитель матрицы есть алгебраическая сумма произведенийn различных элементов матрицы.

Следовательно, что характеристическое уравнение является многочленом от λ, а собственные числа есть корни этого многочлена.

det(A-λE)=(а11- λ)(а22- λ)…(аnn- λ)+..= (1)

Предположим λ=0, det(A-0E)= detA=Ао.

Наше характеристическое уравнение примет вид =0

Многочлен в (2) называется характеристическим многочленом матрицы А