Вычисление определителей специального вида

1. Определитель треугольного вида (элементы под главной диагональю равны нулю):

,т.е. равен произведению элементов главной диагонали (разлагали определители по элементам 1-го столбца).

2. Вычисление блочного определителя:

Доказательство. Применим метод математической индукции по n:

а) при n=1 имеем (разлагая по первому столбцу) ;

б) предположим, что равенство верно для n;

в) докажем, что равенство верно для n+1. Разложим |D| по 1-му столбцу:

По предположению индукции б) (каждый минор определителя |D| есть блочный определитель, где роль А играет определитель порядка n, а роль В играет В) имеем , где – минор матрицы А. Тогда , ч.т.д.

3. Показать, что , где .

4. Показать, что , где .

5. Показать, что , где .

Ранг матрицы

Пусть А=матрица с. Строки – это векторы.

Опр. Максимальное число линейно независимых строк матрицы А называется рангом матрицы А.

Теорема. Ранг матрицы А равен наибольшему порядку миноров матрицы А, отличных от нуля.

Док-во: Пусть наибольший порядок минора, отличного от нуля, равен r. Не уменьшая общности считаем, что этот минор образуется элементами первых r строк и первых r столбцов (т.е. находится в левом верхнем углу). Иначе переставляем строки-векторы. При перенумерации векторов система векторов не имеет ранга. Далее переставляем у всех векторов координаты (т.е. перенумеруем их). Это также не влияет на ранг. Итак, пусть Рассмотрим определитель

Имеем , если 1(ибо содержит две одинаковые строки);, если(т.к. содержит два одинаковых столбца);, еслиk>r,g>r (ибо миноров, отличных от нуля порядка r+1 быть не может). Итак, всегда. Разложим его по последнему столбцу:. Значит,,j = 1,2,…,n.

Отсюда получим, что k-я строка (k>r), т.е. вектор -линейная комбинация первыхr векторов-строк: .

Значит, ранг матрицы не может быть больше r. Если бы ранг был меньше r, то первые r строк матрицы оказались бы линейно зависимыми. Тогда строки определителя (минора) М тем более были бы линейно зависимыми. По теореме ( Если линейно зависима, то существует, равной линейной комбинации остальных ) нашлась бы строка, равная линейной комбинации остальных строк. Вычитая из этой строки линейную комбинацию остальных, мы получили бы определитель с нулевой строкой. Он равен нулю. С другой стороны, определитель не меняется, т.е равен М. Значит, ранг меньшеr быть не может. Итак, ранг матрицы А равен r.

Следствие. Ранг матрицы по столбцам ( максимальное число линейно независимых столбцов) матрицы равен рангу матрицы по строкам (т.е. рангу матрицы).

Методы нахождения ранга матрицы.

1-й способ: Доказательство теоремы о ранге матрицы дает метод нахождения ранга с помощью окаймляющих миноров. Если найдется минор r-го порядка, отличный от нуля, а все окаймляющие его миноры (r+1)-порядка равны нулю, то ранг матрицы равен r.

Пример. Найдем ранг матрицы А=

Минор = -2+3=10. Значит, к2.

Окаймляющий минор = -8+0-20-0+16+12=0

Другой окаймляющий минор 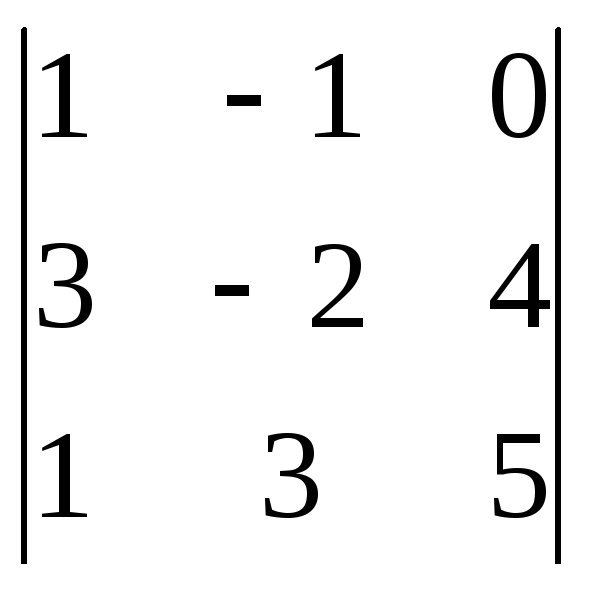= -10+0-4-0-12+15= -110. Значит,r3.

Окаймляющий минор .

Других миноров 4-го порядка нет. Значит, r<4. Тогда к=3.

2-й способ: В силу теоремы ( Если линейно независима, то прибавление к элементу линейной комбинации остальных приводит к линейно независимой системе ) при элементарных преобразованиях строк ранг матрицы не меняется. По этой причине ранг матрицы можно найти с помощью элементарных преобразований строк (или столбцов), приводя матрицу к ступенчатому виду. Число нулевых строк такой матрицы будет равен рангу.

Пример: А=. Прибавим ко второй строке 1-ю, умноженную на (-2), к 3-й строке прибавим 1-ю. Получим . Вычитая из 3-й строки 2-ю получим. Значит, ранг равен 2.