Уравнения математической физики

68Классификации уравнений второго порядка с n независимыми переменными.

Опр. Дифференциальные уравнения, содержащие частные производные, будем называть уравнениями в частных производных. Здесь неизвестная функция u=u(x, y), u=u(x, y, z),…, ,…, , t – время.

Классификация уравнений второго порядка

Рассмотрим . (1)

Пусть x=(x₁, …, x_n) принадлежит области G, a_ij, f определены для xG.

Теорема. Для любой точки x₀ G существует замена переменных =Tx, где , T – матрица, T={t_ij} при которой уравнение (1) перейдет в уравнение вида

, (2)

где v()=u(x()) новая неизвестная функция, а числа A_ij равные 1, -1 или 0, причем количество нулей и разность между положительными и отрицательными числами A_ij не зависит от замены.

(2) – называется каноническим видом уравнения (1).

Доказательство.

(1) перейдет в . Обозначим . Тогда . Пусть A^’={A^’_pq} – матрица .

Вывод. Коэффициенты уравнения (1) при замене =Tx меняется как коэффициенты квадратичной формы: .

Из теоремы о сохранении индекса инерции квадратичной формы и следует утверждение теоремы.

Теорема доказано.

Пояснения. C=AB

D={}=TA

элементы матрицы .

Опр. Уравнение (1) называется:

а) эллиптическим в точке x₀, если в (2) ;

б) гиперболическим в точке x₀, если ;

в) параболическим в точке x₀, если .

Замечание. Классификация является полной только при n=2 u=u(x,y)

а) ; б) ; в) .

При больших n:

- эллиптический тип

- не является ни эллиптическим, ни гиперболическим, ни параболическим.

69.Классификация уравнений второго порядка с двумя независимыми переменными

(1)

Пусть (x,y) D.

Задача. Определить тип уравнения (1) во всех точках области D.

Пример.

Замена , y>0.

u(x,y)=u(x,y(z))=v(x,z)v(x,z(y))=u

// делим на y0

// =2/3

Вывод. Эллиптично для y>0

y=0 – параболический тип

y<0 - гиперболический тип

эллиптический тип

параболический тип

гиперболический тип

(1)

Сделаем замену переменных: .

При этом u(x(,), y(,))=v(,)

v((x, y), (x, y))=u(x, y)

(+ слагаемое с )

/а

/2b

/с

Подставим в (1):

(2)

Рассмотрим вспомогательное уравнение:

=(x, y) (3)

,

(4)

(4) – уравнение в частных производных первого порядка.

Для себя:

Пусть (x, y) D.

Теорема1. Пусть для . Тогда уравнение (1) гиперболическое в D и приводится к виду

(*)

Доказательство. Сделаем замену

- решения (4).

Находим .

В силу (3) коэффициенты перед и равны нулю. Разделим (2) на коэффициент (он не равен 0, поскольку (2) – уравнение второго порядка): . Проверим обратимость замены, что . Если J=0, то :,

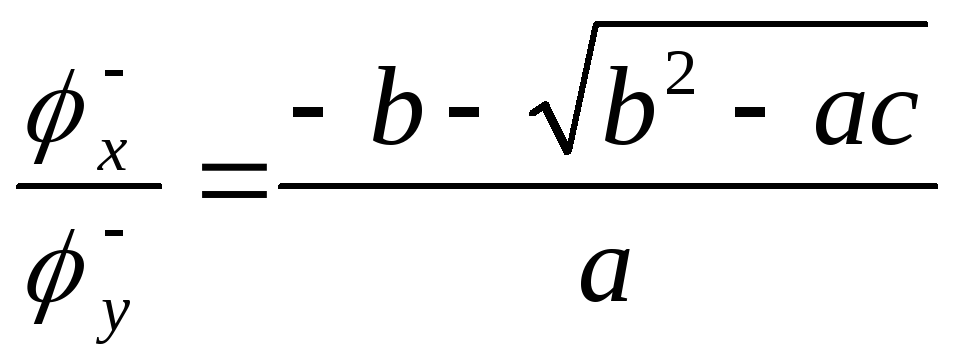
, т.к. преобразование обратимо.

Проверим, что уравнение (*) гиперболического типа. Сделаем замену x=+, y=-

v((x, y),(x, y))=w(x, y), w(x(,), y(,))=v(,)

Уравнение (*) перейдет в уравнение - гиперболического типа.

Теорема2. Пусть . Тогда уравнение (1) параболическое и приводится к виду:

.

Доказательство. Сделаем замену , где , - произвольная аналитическая функция такая, что .

Вычислим коэффициент перед :

.

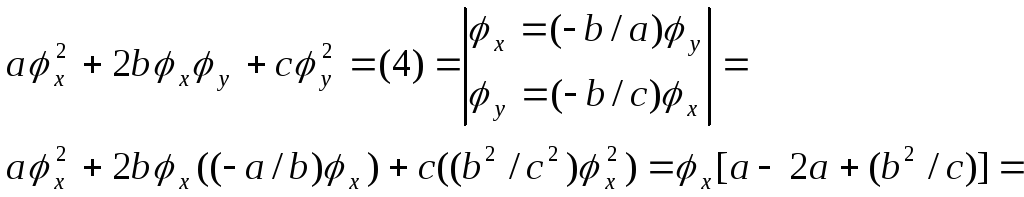
Вычислим коэффициент перед :

+. Разделив (2) на коэффициент перед , получим уравнение .

Теорема3. Пусть . Тогда уравнение (1) эллиптическое и приводится к виду

.

Доказательство. (4) имеет два комплекснозначных решения , причем . Пусть , где - вещественные функции.

Сделаем замену в (1) с =(x, y), =(x, y).

Подставим в (4). Тогда действительная часть Re:

, . (5)

, где . Из теории уравнений первого порядка существует единственное решение системы (5), если задача начальное условие.

Подставим в (3):

.

Re:

В результате замены =, = коэффициенты перед совпадают.

Im:

коэффициент перед равен 0.

Поделим (2) на коэффициент перед , получим .

Докажем обратимость замены =(x, y), =(x, y).

Вычислим

.

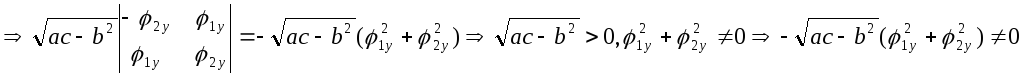Если =0 из (5) , ; =const, = const (этот случай исключен). Ч.т.д.

70. Существование и единственность решения задачи Коши для уравнения колебаний неограниченной струны

(6)

Неограниченная струна с физической точки зрения является идеализацией, означающей, что мы рассматриваем внутренний участок струны, считая концы достаточно далёкими, так что на рассматриваемом интервале времени они не влияют на происходящее на данном участке струны.

Рассмотрим одномерное волновое уравнение (6) при х € R, t >= 0. Естественной задачей здесь является задача Коши: задача о нахождении решения уравнения (6) с начальными условиями (18)

С физической точки зрения условия (18) означают, что заданы начальное положение и начальная скорость струны. Можно ожидать, что по аналогии с конечномерными задачами механики задача Коши здесь будет корректна, т.е. решение существует, единственно и непрерывно зависит от начальных данных и . Как мы увидим сейчас, это действительно так.Воспользуемся общим решением уравнения (6):

u(t,x)=f(x-at)+g(x+at). (19)

Записывая условия (18), получим систему двух уравнений для определения произвольных функций f и g: (20)

Интегрирование второго уравнения дает

(21)Из (20) и(21) находим

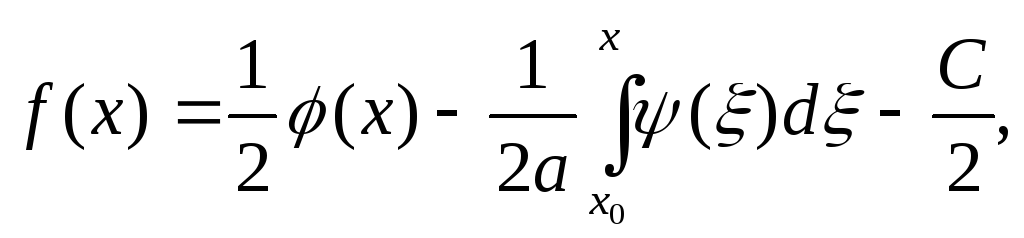(22)

Поэтому

Или (24)

Итак, решение u(t, x) действительно существует, единственно и непрерывно зависит от начальных данных при разумном выборе топологий в множестве начальных данных и функций u(t,x). Например, ясно, что если решение построено по начальным данным и при достаточно малом 6 > 0

(25)

То (26)

Со сколь угодно малым >0. Таким образом задача Коши корректна.

Формула (24), задающая решение задачи Коши, называется формулой Даламбера.Сделаем несколько замечаний по поводу её вывода и применений.

Во-первых, заметим, что эта формула имеет смысл для любых локально интегрируемых функций , давая обобщённое решение уравнения (6). Мы будем рассматривать лишь непрерывные решения. Тогда в качестве можно брать любую непрерывную функцию,а в качестве - любую локально интегрируемую. Получаемые таким образом функции u(t, х) естественно называть обобщёниыми решениями задачи Коши. Мы будем рассматривать обобщённые решения наравне с обычными, опуская слово «обобщенный».

Во-вторых, из формулы Даламбера ясно, что значение решения в точке t₀, зависит лишь от значений при и от значений при Отрезок [] высекается на оси х в (t,x)-пространстве характеристиками, проходящими через точку (to, хо). Образованный этими характеристиками и осью х, треугольник образует множество тех точек полуплоскости t>=0 в которых значение решения полностью определяется начальными данными на отрезке [] (этот треугольник называется областью заѳисимости для отрезка []). Элементарный анализ вывода формулы Даламбера показывает, что она верна для любого решения, определённого в треугольнике, у которого боковыми сторонами являются характеристики, а нижнее основание - отрезок [с, d] оси х (т. е. не обязательно требовать, чтобы решение было определено всюду в полуплоскости t >=0). В самом деле, из уравнений (20), мы находим значения f(x) и g(x) при х € [с, d] (если начальные данные определены на [с, d]). Ho это даёт значения u(t, x) при х - at € [с, d], x+at € [с, d], т. е. когда проведенные через точку (t, x) характеристики пересекают отрезок [с, d] на оси х. При этом, конечно, можно считать, что f(х) и g(х) определены только на [с, d] (т.е. u(t, x) определена в указанном треугольнике, являющемся областью зависимости отрезка [с, d]). Физический смысл области зависимости очевиден: она состоит из тех точек (t, x), для которых волна, движущаяся со скоростью a от одного из концов отрезка [с, d] и начавшая движение при t= 0, не успевает за время t дойти до точки х.

Далее, значения начальных данных и на [с, d] не влияют на значение u(t, х), если x+at< с или x-at > d (т. е. волна за время t не успевает дойти от ближайшего к точке х конца отрезка [с, d] до точки х]. Поэтому область, ограниченная отрезком [с, d] и лучами прямых x + at = с, х- at= d, лежащими в полуплоскости t >=0, называется областью влилния отрезка [с,d]. Эта область является дополнением множества тех точек ( t, x ), для которых u(t, x) не зависит от значений и на [с, d].