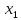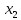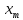83 Генеральная и выборочная совокупности. Статистическое распределение выборки. Эмпирическая функция распределения выборки. Полигон и гистограмма частот.
Генеральной совокупностью называется совокупность объетов или наблюдений, все элементы которой подлежат изучению при статистическом анализе. Генеральная совокупность может быть конечной или бесконечной.
На практике изучение всего набора элементов генеральной совокупности в большинстве случаев оказывается невозможным. Часть объектов генеральнойсовокупности, используемая для исследования, называется выборочной совокупностью или выборкой (X). Число объектов в генеральной совокупности (N ) или выборке (n) называют их объемами. В примере об исследовании спроса на размерымужской обуви используется выборка объема n = 350, в примере об исследовании точности измерительного прибора n = 50 . Сущность выборочногометода состоит в том, что выводы, сделанные на основе изучения части совокупности (выборки), статистика позволяет распространять на всю генеральную совокупность.
Эмпирической
функцией распределения (функцией
распределения выборки)
называют функцию
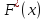, которая равна относительной частоте
появления события {X<x},
найденную по данной выборке
,
где n(x) - количество вариант, меньших x; n - объем выборки.
Для нахождения эмпирической функции распределения выборки удобнее сначала вычислить относительные частоты попадания случайной величины в i- тый интервал
.
Затем вычислить
накопленные относительные частоты
- сумму относительных частот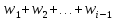
.Результаты
вычислений записывают в виде таблицы
Таблица 1. Распределение относительных частот
Из таблицы 1 находим эмпирическую функцию распределения
Эмпирическая функция распределения обладает теми же свойствами, как и функция распределения дискретной случайной величины.
|
|
|
|
|
|
… |
|
- |
|
|
|
|
|
|
… |
|
|
|
Накопленные
относительные частоты
|
0 |
|
|
|
|
|
1, при X> |
Используя таблицы
(1) и (2) можно построить полигон частот
и полигон относительных частот.
Полигоном
частот
называют ломаную, соединяющую точки с
координатами
,полигоном
относительных частот –
ломаную
.
Гистограммой
частот (относительных частот)
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длины ℎ,
а высоты равны отношению
.
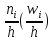Очевидно, что вся площадь гистограммы
частот равнаn,
а площадь гистограммы относительных
частот равна единице.
Гистограмма
относительных частот, построенная на
основе выборки, может служить оценкой
неизвестной плотности вероятностей.
При увеличении объема выборки и
уменьшении длин интервалов гистограмма
относительных частот приближается к
графику неизвестной функции плотности
вероятности генеральной совокупности
.
По виду гистограммы или полигона частот можно выдвинуть гипотезу о виде распределения генеральной совокупности.