17. Дифференцируемость функции многих переменных. Частные производные. Связь между дифференцируемостью и непрерывностью частных производных.

Производные и дифференциалы функции нескольких переменных.

Пусть точка М (х₁, x₂, …. , x_m) является внутренней точкой области задания функции u = f (х₁, x₂, …. , x_m). Рассмотрим в данной фиксированной точке М (х₁, x₂, …. , x_m) отношение частного приращения _xku к соответствующему приращению _xk аргумента x_k:

(14.12)

Отношение (14.12) представляет собой функцию от , определенную для всех, отличных от нуля значений, для которых точка Мпринадлежит области задания функции u.

Опр Если существует предел отношения (14.12) частного приращения и функции в точкеM (x₁, x₂, … , x_m) к соответствующему приращению аргументаx_k при 0, то этот предел называетсячастной производной функции u = f (x₁, x₂, … , x_m) в точке М по аргументу x_k и обозначается одним из следующих символов:

Таким образом,

Замечание 1: Из существования в данной точке всех частных производных, вообще говоря, не вытекает непрерывность функции в этой точке.

Замечание 2: Описанное выше понятие частных производных, вообще говоря, для граничных точек является непригодным.

Понятие дифференцируемости функции нескольких переменных:

Полным приращением функции называется

u = f (x₁ + x_1, x₂+x₂, ………., x_m+x_m) – f (x₁, x₂, …., x_m)

Опр Функция u = f (x₁, x₂, …., x_m) называется дифференцируемой в данной точке М (x₁, x₂, …., x_m), если ее полное приращение в этой точке может быть представлено в виде

u = A₁x₁ + A₂x₂+…+ A_mx_m+ ₁x₁+ ₂x₂+….+ _mx_m, (14.14)

где А₁, А₂, …, А_m – некоторые не зависящие от x₁ , x₂,…, x_m число, ₁ , ₂ ,…., _m – бесконечно малые при x₁ , x₂,…, x_m функции, равные нулю, при x₁ = x₂=…= x_m = 0. Соотношение (14.14) называется условием дифференцируемости функции в данной точке М.

Условие дифференцируемости можно записать также в иной форме. Для этого рассмотрим бесконечно малую при x₁ , x₂,…, x_mфункцию p=и отметим, что эта функция обращается в нуль лишь приx₁ = x₂=…= x_m = 0. Убедимся теперь, что входящая в правую часть соотношения (14.14) сумма ₁x₁+ ₂x₂+….+ _mx_m представляет собой бесконечно малую более высокого порядка функцию по сравнению с р. Иными словами, убедимся, что эта сумма представляет собой выражение о(р). В самом деле, при р0 справедливо1, и поэтому

|₁x₁+ ₂x₂+….+ _mx_m | {|₁+ ₂+….+ _m|} {|₁|+|₂|+…+|_m|}, p=o(p).

Таким образом, условие (14.14) дифференцируемости функции может быть записано в следующей форме:

u = A₁x₁ + A₂x₂+…+ A_mx_m+ о(р), (14.15)

При это величину о(р) мы считаем равной нулю при р = о.

Условия (14.14 ) и (14.15) эквивалентны.

Теорема 14.9 Если функция u = f (x₁, x₂, …. , x_m) дифференцируема в точке М (x₁, x₂, …. , x_m), то в этой точке существует частные производные по всем аргументам, причем =А_i, где А_i определяются из условия (14.14) и (14.15) дифференцируемости функции.

Док-во: Из условии (14.14) дифференцируемости функции в точке М (x₁, x₂, …. , x_m) вытекает, что ее частное приращение x_i u и в этой точке равно x_i u = Аx_i +x_i. Отсюда вытекает, что = А_i +, и поэтому, т.к.приx_i ,.

Следствие 1: Условие (14.15) дифференцируемости функции в данной точке М можно записать в следующей форме:

(14.16)

Следствие 2: Если функция u = f (x₁, x₂, …. , x_m) дифференцируема в точке М (x₁, x₂, …. , x_m), то представление ее приращения u и в форме (14.14) и (14.15) единственно.

Свойство: Если функция u = f (x₁, x₂, …. , x_m) дифференцируема в точке М (x₁, x₂, …. , x_m), то она и непрерывна в этой точке.

В случае функции u = f (х,у) 2-х переменных условие дифференцируемости может быть иллюстрировано геометрически. Введем понятие касательной плоскости к поверхности в точке N₀. Плоскость , проходящая через точку N₀ поверхности, называется касательной плоскостью в этой точке, если угол между этой плоскостью и секущей, проходящей через точку N₀ и любую точку N₁ поверхности, стремится к нулю, когда точка N₁ стремится к N₀.

Уравнение касательной плоскости:

U – u₀ = (14.17)

Нормальный вектор n = касательной плоскости принято называть нормалью к поверхности u = f (х,у) в точкеN₀ (x₀, y₀, u₀).

Достаточное условие дифференцируемости :

Теорема 14.10 Если функция u = f (x₁, x₂, …. , x_m) имеет частные производные по всем аргументам в некоторой окрестности точки М (x₁, x₂, …. , x_m), причем все эти частные производные непрерывны в самой точке М₀, то указанная функция дифференцируема в точке М₀.

Док-во: Для сокращения записи проведем док-во для функции 2-х переменных u = f (х,у). Итак, пусть обе частные производные f ^|_x и f ^||_y существует в окрестности точки М₀(x₀, y₀) и непрерывны в этой точке. Дадим аргументам х и у столь малые приращения х иу, чтобы точка М(х₀+х, у₀+у) не выходила за пределы указанной окрестности точки М₀. Полное приращение u = f (х₀+х, у₀+у)-f (х₀,у₀) можно записать в виде

u = [ f (х₀+х, у₀+у) - f (х₀, у₀+у)] + [f (х₀, у₀+у) –f(х₀,у₀)].

Выражение [ f (х₀+х, у₀+у) - f (х₀, у₀+у)] можно рассматривать как приращение функции f (х₀, у₀+у) одной переменной х на сегменте [x,х₀+х]. Поскольку функция u= f (х,у) имеет частные производные, указанная функция f (х, у₀+у) дифференцируема и ее производная по х представляет собой частную производную f^|_{x .} Применяя к указанному приращению формулу Лагранжа, найдем такое ₁ из интервала 0<₁ <1, что

[ f (х₀+х, у₀+у) - f (х₀, у₀+у)] = f^|_x (х₀+₁, у₀+у)х.

Рассуждая совершенно аналогично, получим, что для некоторого ₂ из интервала 0<₂ <1,

[ f (х₀, у₀+у) - f (х₀, у₀)] = f ^|_у (х₀, у₀+₂у)у.

Так как производные f ^|_x и f ^|_у непрерывна в точке М₀, то

f ^|_x (х₀+₁, у₀+у) = f^|_x (х₀, у₀) + ,

f ^|_у (х₀, у₀+₂у)у= f^|_у (х₀, у₀)+,

где и- бесконечно малые прихиуфункции. Отсюда, учитывая приведенные выражения для

[ f (х₀+х, у₀+у) - f (х₀, у₀+у)] и [f (х₀, у₀+у) –f(х₀,у₀)]

и выражения для u, найдем

u = f ^|_х (х₀, у₀) х + f^|_у (х₀, у₀) у +.

Следовательно, функция u = f (х,у) дифференцируема в точке М₀. В случае функции m переменных u = f (x₁, x₂, …. , x_m) рассуждения проводятся аналогично, только полное приращение u этой функции следует представить в виде суммы

u = f () – f () =-f()

(все х тоже с точками, только чё-то не поставилось!)

Теорема доказана.

Следствие: Если функция u = f (x₁, x₂, … , x_m) дифференцируема в точке М (x₁, x₂, …. , x_m), то она и непрерывна в этой точке.

Теорема (С Амангильдина): Если функция u = f (x₁, x₂, … , x_m) имеет частные производные по всем аргументам в некоторой окрестности точки М (x₁⁰, x₂⁰, …. , x_m⁰), причем все эти частные производные непрерывны в самой точке М₀, то указанная функция дифференцируема в точке М₀.

Понятие дифференциала функции нескольких переменных.

Опр. Дифференциалом du дифференцируемой в точке М (x₁, x₂, …. , x_m), функции u = f (x₁, x₂, …. , x_m) называется главная линейная относительно приращенной аргументов часть приращения этой функции в точке М. Если все коэффициенты А_i в представлении (14.14) приращения дифференцируемой функции равны нулю, то дифференциал du функции в точке М считается равным нулю.

Таким образом, дифференциалом du дифференцируемой в точке М функции u = f (x₁, x₂, …. , x_m) называется выражение

du = A₁x₁ + A₂x₂+…+ A_mx_m (14.18)

Используя теорему 14.9, мы можем, очевидно, переписать выражение (14.18) для дифференциала du следующим образом:

(14.19)

Введем понятие дифференциала dx_i независимой переменной x_i можно понимать любое (не зависящее от x₁, x₂, …. , x_m) число. Договоримся в дальнейшем брать это число равным приращению x_i независимой переменной x_i. Эта договоренность позволяет нам переписать формулу (14.19) в виде

(14.20)

Подчеркнем, что формула (14.20) установлена нами лишь для случая, когда аргументы x₁, x₂, …. , x_m являются независимыми переменными. Однако эта формула остается справедлива и для случая, когда аргументы x₁, x₂, …. , x_m не являются независимыми.

Дифференцирование сложной функции:

В этом пункте мы рассмотрим вопрос о дифференцировании сложной функции вида u = f (x₁, x₂, …. , x_m), где

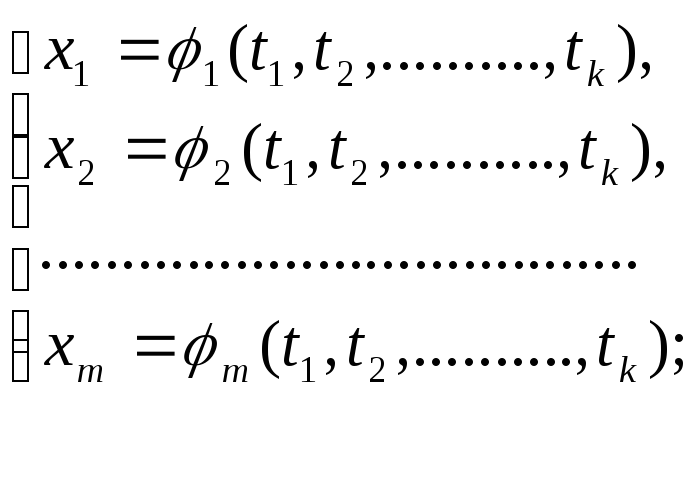(14.21)

Мы докажем, что при определенных условиях эта сложная функция является дифференцируемой функцией своих аргументов t₁, t₂, …. , t_k. При этом частные производные указанной сложной функции по аргументам t₁, t₂, …. , t_k выражается через частные производные функции u = f (x₁, x₂, …. , x_m) и через частные производные функций (14.21) по следующим формулам:

14.22)

Теорема 14.11 Пусть функции (14.21) дифференцируемы в некоторой точке М(), а функция u = f (x₁, x₂, …. , x_m) дифференцируема в соответствующей точке N (), где,i=1,2,…,m. Тогда сложная функция u = f (x₁, x₂, …. , x_m), где x₁, x₂, …. , x_m определяются соотношениями (14.21), дифференцируема в точке М. При этом частные производные этой сложной функции в точке М определяются формулами (14.22), в которых все частные производные берутся в точке N, а все частные производныефункции (14.21) по аргументамt₁, t₂, …. , t_k берутся в точке М.

Теорема 14.12 (теорема Эйлера об однородных функциях).

Если u = f (x₁, x₂, …. , x_m) является в некоторой области { М } дифференцируемой однородной функций степени р, то в каждой точке М(x₁, x₂, …. , x_m) области { М } справедливо равенство