ШПОРЫ ПО ФИЗИКИ / Максвелловское распределение частиц по скоростям

Максвелловское распределение частиц по скоростям:

Пусть моле­кула А имеет скорость u₁, равную по модулю u и направленную вдоль оси ОХ. После упругого столкновения с другой молекулой, движущейся с такой же по модулю скоро­стью u₂ вдоль оси OZ, молекула А может получить дополнительную скорость u₂ (рис). В результате такого столкнове­ния вторая молекула останавливается, а скорость молекулы А становится равной u'₁=u₁+u₂, так что u'₁=2u. Закон распределения по скоростям теп­лового движения молекул газа, находяще­гося в состоянии термодинамического рав­новесия, впервые был найден Д. К. Мак­свеллом (1859) и называется распределени­ем Максвелла. Ход рассуждений Максвелла достаточно сложен, и приводить его мы не будем, а ограничимся рассмотрением физи­ческого смысла закона Максвелла и некото­рых его следствий.

Скорости молекул удобно изображать в виде полярных векторов в трехмерном пространстве скоростей, в котором по вза­имно ортогональным осям координат отло­жены компоненты u_x, u_y и u_z скоростей мо­лекул (рис 2). Пусть dn – число моле­кул в единице объема газа, модули скоростей которых заключены в пределах от u до u+du. Очевидно, что концы векто­ров скоростей этих молекул должны лежать в пространстве скоростей внутри шарового слоя, закрашенного на (рис 2). Объем этого слоя d=4u²du. При тепловом дви­жении из-за его беспорядочности все направления скоростей молекул равновероят­ны. Поэтому число dn должно быть пропор­ционально как числу молекул в единице объема газа, так и объему d шарового слоя. Кроме того, dn должно зависеть от модуля скорости u. Таким образом,

где

Функция распределения

представляет собой долю молекул, модули скоростей которых находятся в шаровом слое единичной толщины. Произведение

F (u) du=dn/n₀ есть вероятность того, что модуль скорости молекулы заключен меж­ду u и u+du. Функция F (u) наз. функцией распределения молекул газа по модулям их скоростей. Закон распределения молекул по скоростям (закон Максвелла):

Наиболее вероятная скорость:

Средняя арифметическая скорость:

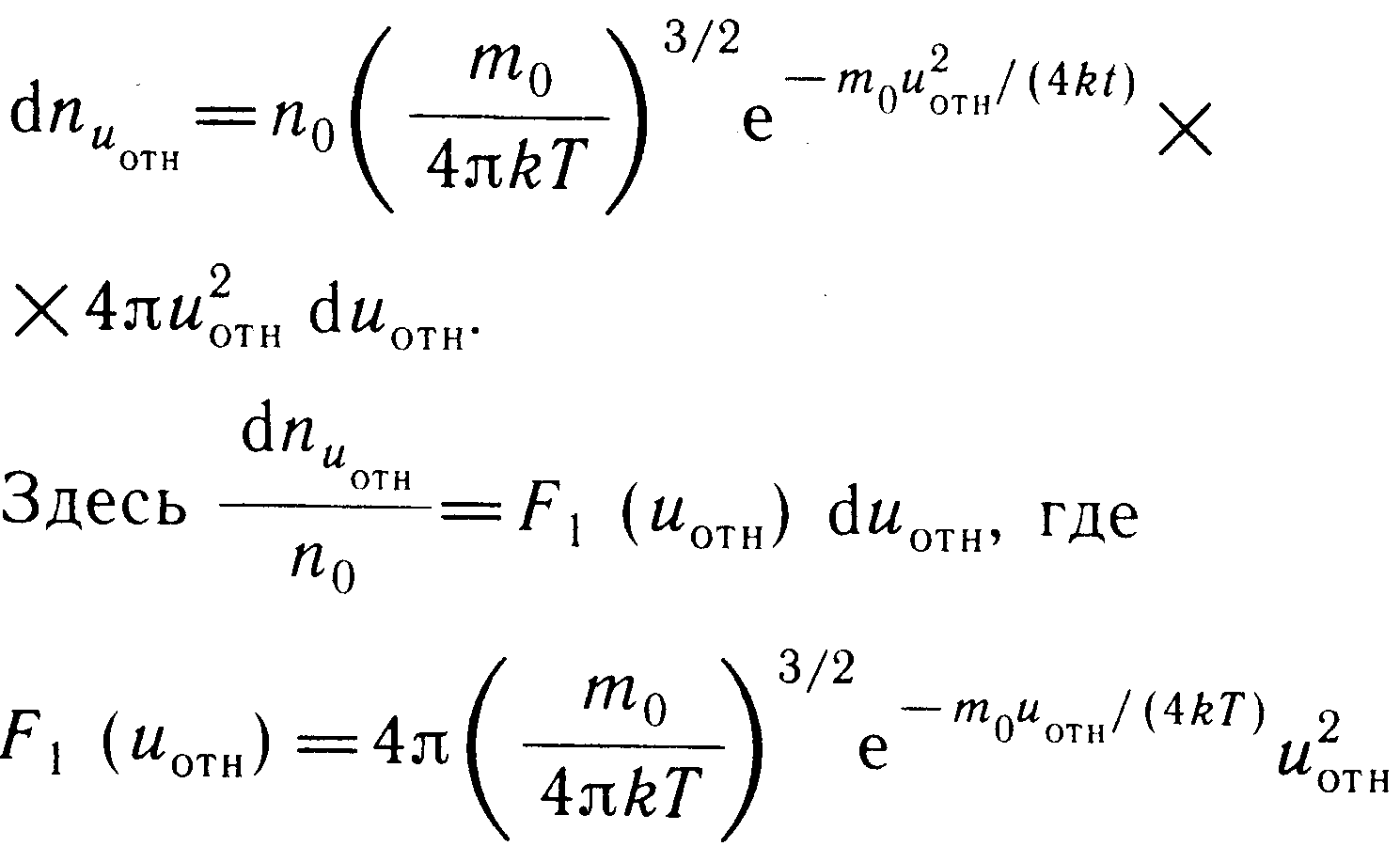Распределение молекул по относительным скоростям:

– функция распределения молекул идеального газа по относительным скоростям.

Средняя относительная скорость: