
Gmail / Механика-5
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ТРЕНИЯ СКОЛЬЖЕНИЯ И ТРЕНИЯ КАЧЕНИЯ С ПОМОЩЬЮ НАКЛОННОГО МАЯТНИКА
ЛАБОРАТОРНАЯ РАБОТА ПО МЕХАНИКЕ № 5
для студентов естественных факультетов и физико-технического института
Уфа РИО БашГУ 2013
Печатается по решению кафедры общей физики: протокол № 3 от 27 декабря 2012 г.
Составители: к.ф.-м.н., доц. Акманова Г.Р. асс. Шафеев Р.Р.
2
ЛАБОРАТОРНАЯ РАБОТА №5 Определение коэффициентов трения скольжения и трения
качения с помощью наклонного мятника
Приборы и принадлежности: установка ФМ16, маятник качения, мятник скольжения, сменные пластины, сменные шары, шары усеченные из различных материалов (сталь, латунь, алюминий).
Цель работы: 1.Определение коэффициентов трения качения. 2.Определение коэффициентов трения скольжения.
КРАТКАЯ ТЕОРИЯ
Силы трения появляются при перемещении соприкасающихся тел (или их частей) друг относительно друга. Трение, возникающее при относительном перемещении двух соприкасающихся тел, называется внешним; трение между частями одного и того же сплошного тела (например, жидкости или газа) носит название внутреннего трения.
Трение между поверхностями двух соприкасающихся твердых тел при отсутствии между ними жидкой (или газообразной) прослойки (смазки) называется сухим.
Трение между телом и жидкой (или газообразной) средой, а так же между слоями такой среды называется вязким (или жидким).
В данной работе изучаются законы сухого трения. Различают три вида сухого трения: трение покоя, трение скольжения и трение качения.
Сухое трение возникает не только при скольжении одного тела по поверхности другого, но и при всякой попытке вызвать такое скольжение. Трение, возникающее при попытке вызвать движение одного тела по поверхности другого, называется трением покоя или трением сцепления.
Пусть на горизонтальной поверхности находится тело. Приложим к нему переменную горизонтальную силу. Можно убедиться, что не любая приложенная к телу сила может вызвать её скольжение по поверхности. Это отсутствие движения можно объяснить тем, что приложенная сила уравновешивается какой-то другой силой. Этой силой является сила трения покоя. Таким образом, сила трения покоя автоматически принимает значение приложенной силы.
3

Приложенную силу данного направления можно менять в принципе от нуля до сколь угодно большого значения, а сила трения покоя имеет предельное значение, которое называется максимальной силой трения покоя. Максимальная сила трения покоя выражается формулой, установленной опытным путём французским учёным Амонтоном ещё в 1699 году:
F0 kN |
(1) |
где k – коэффициент трения покоя, зависит от свойств (физической природы и качества обработки) поверхностей соприкасающихся тел; N – сила нормального давления.
До тех пор, пока внешняя сила не превосходит максимальную силу трения покоя F0 , скольжение не возникает (явление застоя). Если сила F , действующая на тело, больше максимальной силы трения покоя (F > F0), начинается скольжение и сила трения покоя переходит в силу трения скольжения.
Тело получает ускорение a F F0  m, скорость его начинает
m, скорость его начинает
расти.
В общем случае сила трения при скольжении зависит от относительной скорости трущихся тел. Характер этой зависимости различен для различных пар трущихся тел. в некоторых случаях зависимость силы трения от скорости может иметь вид, приведённый на
рис.1. Как видно из графика, для некоторого интервала при малых скоростях силу трения скольжения можно считать постоянной, не зависящей от скорости и равной максимальной силе трения покоя (закон Кулона, установленный в 1781 году). Опыты подтверждают
4

это с достаточной точностью. В этом случае характер зависимости силы трения от скорости имеет вид на рис.2.
Закон Кулона для силы трения скольжения имеет вид:
FТр kN , |
(2) |
где k – коэффициент силы трения скольжения, равный коэффициенту силы трения покоя. Как видно из (2), коэффициент k не имеет размерности. Законы Амонтона и Кулона являются приближёнными, т.к. коэффициент трения k зависит не только от физической природы и качества обработки поверхностей трущихся тел, но также от загрязнений, давления между телами, от температуры и т.п. Кроме того, k зависит от большого числа причин, многие из которых не поддаются учёту (наличие на соприкасающихся поверхностях окислов, влаги, адсорбированных газов и др.). Поэтому результаты изменений коэффициентов трения скольжения, полученные для одних и тех же материалов в разных опытах, могут противоречить друг другу. Причиной, вызывающей силу трения (покоя и скольжения) между грубо обработанными поверхностями, является возникновение сил при зацеплении неровностей (выступов и впадин). Эти силы направлены в сторону, противоположную действующей силе. При улучшении качества обработки поверхностей сила трения уменьшается, однако в случае идеально гладких поверхностей сила трения может стать бесконечно большой (поверхности прилипнут друг к другу), вследствие молекулярного (или атомного сцепления).
Распространенным методом определения коэффициента трения скольжения (а также коэффициента трения покоя) является метод предельного угла. Пусть тело находится на наклонной плоскости (угол наклона ) (рис.3). На тело вдоль наклонной плоскости действует составляющая силы тяжести
Psin , однако скольжение наблюдается с определенного (предельного) угла 0 . Следовательно, при отсутствии движения сила Psin уравновешивается с силой трения покоя F.
5

F Psin |
(3) |
При предельном угле 0 , начинается скольжение, т.е. трение покоя переходит в трение скольжения Fтр .
Согласно (2),
FТр kN kmgcos |
(4) |
Тогда при = 0 (3) и (4) дают |
|
k tg 0 |
(5) |
Рассмотрим теперь механизм возникновения трения качения (без скольжения). Тело (цилиндр или шар), катящееся по ровной горизонтальной поверхности без скольжения, постепенно останавливается под действием силы трения качения, зависящей от физических свойств материалов плоскости и катящегося тела (а так же силы сопротивления воздуха).
При качении тело и плоскость деформируются под действием силы, прижимающей тело к плоскости. Так как для окончательного суждения неважно, что деформируется: тело или плоскость или то и другое, то для простоты рассуждений предположим, что тело (цилиндр или шар) не деформируется, а деформируется только поверхность, по которой катится тело. Какой характер имеет эта деформация?
Допустим деформация носит упругий характер (рис. 4), тогда силы взаимодействия между телом и плоскостью будут совершенно симметричны относительно вертикальной плоскости ab , проходящей через ось тела: каждой силе f с фронтальной стороны катящегося тела будет соответствовать равная ей
сила f′ на симметрично расположенном участке площади соприкосновения с тыльной стороны катящегося тела.
6

Результирующая всех сил упругой деформации поверхности качения будет вертикальна, и сумма моментов этих сил относительно оси тела так же будет равна нулю. Поэтому силы упругих деформаций тела и плоскости при качении не скажутся на скорости качения и движение будет происходить так, как будто никаких деформаций нет. Никаких сил трения качения в этом случае не возникает и тело будет катиться бесконечно долго.
Следовательно, для объяснения сил трения качения следует считать деформации тела и плоскости качения неупругими, что фактически всегда имеет место. Очевидно, что силы, действующие на тело со стороны плоскости качения, не должны быть симметричными относительно плоскости ab: сила f больше силы f′ на симметричном участке, расположенном сзади плоскости ab. Поэтому результирующая этих сил обязательно имеет горизонтальную составляющую, направленную назад и момент этих сил относительно оси цилиндра также не равен нулю, причем он тормозит вращение тела.
Найдём силу трения качения: Точка приложения результирующей не может быть расположена ни в вертикальной плоскости ab , проходящей через центр, ни сзади неё, ибо тогда эта сила
сообщила |
положительное |
|
угловое ускорение телу, т.е. |
||
ускоряла |
бы |
его. |
Следовательно, |
остаётся |
|
последний |
вариант: точка |
|
приложения |
силы |
N |
(реакция опоры) должна находиться впереди, причём линия силы N должна проходить выше центра тела, в противном случае она сообщила бы положительное угловое ускорение. Таким образом, на катящееся тело действует сила трения качения, которая направлена и приложена так, как показано на рис.5.
Горизонтальная компонента силы N представляет силу трения качения fK .Так как расстояние S (расстояние от точки приложения
7
силы N до плоскости ab) практически очень мало по сравнению с радиусом тела R и угол наклона очень мал, то абсолютная величина N почти равна силе давления, прижимающей тело к плоскости, в данном случае силе тяжести тела P . Связь между силой трения качения и другими величинами определяют опытным путём.
Пусть к оси вращения равномерно катящегося по горизонтальной плоскости тела приложена постоянная горизонтальная сила F в направлении движения, равная силе трения качения fK . Так как вращение тела равномерное и угловое ускорение его равно нулю, то сила N должна проходить через ось тела. Две другие силы: сила тяжести P и внешняя сила F по условию проходят через ось тела. Следовательно,
P Ncos , |
FNsin fK . |
(6) |
так как угол мал, то (6) можно записать
P N, |
fK |
N P |
S |
(7) |
|
R |
|||||
|
|
|
|
Обычно говорят не о силе трения качения, а о моменте силы трения качения:
fK R S P |
(8) |
Таким образом, момент силы трения качения равен силе нормального давления P, умноженной на S . Величину S называют коэффициентом трения качения (имеет размерность длины).
Рассмотрим принцип действия наклонного маятника.
Если маятник отклонить вдоль наклонной плоскости на некоторый угол и отпустить, то начнутся колебания, которые будут затухать под действием силы трения маятника о плоскость, силы сопротивления среды и силы трения в подвесе маятника. Основной причиной в данном случае будет интересующее нас трение о плоскость. Двумя другими силами трения можно пренебречь. Пусть масса маятника т. Основные силы, действующие на маятник в отклоненном положении, изображены на рис.6. Их четыре:
8
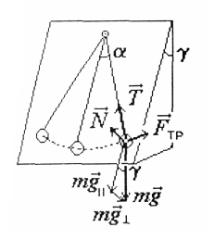
Рис. 6
сила тяжести mg , сила N нормальной реакции плоскости, сила FТр- трения о плоскость и сила Т натяжения подвеса. Сила трения связана с силой реакции плоскости законом (2).
Разложим силу тяжести на компоненты mgII параллельную
плоскости, и mg , |
перпендикулярную плоскости. Сила N |
||||
нормальной |
реакции |
уравновешивает |
компоненту |
mg , |
|
следовательно, |
эти |
два |
вектора равны по величине: |
||
N mg mgsin и для силы трения получается выражение |
|
||||
|
|
Fтр |
kmgsin . |
|
|
Обозначим начальный угол отклонения маятника вдоль плоскости α0, максимальный угол в противоположную сторону (через половину периода) α1/2, угол отклонения через период – α1). При медленном убывании амплитуды потери энергии за каждый период приблизительно одинаковы и α1/2 = (α0+ α1)/2. За период точка касания маятника проходит путь
S =l(α0+ 2α1/2 +α1) = 2l (α0 +α1). При этом сила трения совершает работу:
Aтр FтрS 2kmglsin 0 1 . |
(9) |
9

На величину этой работы уменьшается полная механическая энергия маятника. В крайних положениях эта энергия состоит только из потенциального вклада mgh, поэтому
Aтр mgh0 mgh1 , |
(10) |
где h0, h1 – высоты подъема маятника в крайнем положении, соответствующие углам α0, α1. С помощью рисунка 7 найдем, как высота подъема h связана с углом α отклонения маятника. В отклоненном положении центр тяжести маятника поднят вдоль плоскости на отрезок
BD = АС = l (1 – cosα). Из треугольника BDE получаем:
h = BDcosγ = l cosγ (l – cosα)= 2lcosγsin2 (α/2) ≈ lcosγα2/2.
Последнее приближенное равенство справедливо при малых углах, в этом случае sin(α/2) ≈ α/2. Подставляя выражение для каждой из высот в уравнение (10) и учитывая формулу (9) получим:
-2mgl sin γ(α0 + α1) = mglsin γ(α12/2 – α02/2)
Рис.7.
10
