
Gmail / Механика-10
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИЗУЧЕНИЕ ЗАКОНА СОХРАНЕНИЯ
ИМПУЛЬСА
ЛАБОРАТОРНАЯ РАБОТА ПО МЕХАНИКЕ № 10
для студентов естественных факультетов и физико-технического института
Уфа РИО БашГУ 2013
Печатается по решению кафедры общей физики: протокол № 3 от 27 декабря 2012 г.
Составители: к.ф.-м.н., доц. Акманова Г.Р. асс. Шафеев Р.Р.
2
ЛАБОРАТОРНАЯ РАБОТА №10 ИЗУЧЕНИЕ ЗАКОНА СОХРАНЕНИЯ ИМПУЛЬСА
Приборы и принадлежности: установка ФМ 17, блок электронный, набор шаров (два стальных, алюминиевый, алюминиевый со стальной вставкой, латунный, латунный со стальной вставкой).
Цель работы: 1. Изучение закона сохранения импульса при абсолютно упругом ударе.
2.Определение средней силы соударения шаров.
3.Определение коэффициентов восстановления скорости и энергии для случая упругого удара шаров.
КРАТКАЯ ТЕОРИЯ
Соударением (ударом) в механике называется кратковременное взаимодействие тел, возникающее в результате их соприкосновения и приводящее к значительному изменению состояния их движения. Обычно процесс удара разделяют на две фазы. Первая фаза - с момента соприкосновения тел до момента, когда их относительная скорость становится равной нулю. Вторая фаза - от этого момента до момента, когда соприкосновение тел прекращается.
Пусть два упругих шара движутся навстречу друг другу. В месте соприкосновения шары деформируются. Сила упругости, возникшая в результате деформации первого шара, направлена против движения второго шара, а сила, действующая со стороны второго шара на первый, направлена против движения первого. В результате действия упругих сил скорости шаров уменьшаются до тех пор, пока они не станут одинаковыми, т.е. относительная скорость шаров станет равной нулю. При этом происходит переход части кинетической энергии шаров в потенциальную энергию упругой деформации. На этом первая фаза удара завершается. С этого момента начинается восстановление деформации. Силы упругости, продолжая действовать в прежнем направлении, совершают положительную
3
работу, кинетическая энергия системы шаров растет. Шары расходятся. Завершается вторая фаза удара.
Различают два предельных типа удара: абсолютно неупругий и абсолютно упругий. При абсолютно неупругом ударе имеет место только первая фаза, тела после удара движутся с общей скоростью. Возникающая при этом деформация тел не исчезает, а носит остаточный (пластический) характер.
При абсолютно упругом ударе (ударе абсолютно упругих тел) имеют место обе фазы удара, причем деформации, возникающие в телах при ударе, полностью исчезают и кинетическая энергия системы до удара равна кинетической энергии системы после удара.
Абсолютно упругих ударов в природе не существует, так как всегда часть энергии затрачивается на необратимую деформацию и внутренняя энергия соударяющихся тел увеличивается. Однако в некоторых случаях потерями механической энергии можнопренебречь.
Рассмотрим самый простой случай - центральный удар двух однородных шаров. При центральном ударе скорости шаров до удара направлены вдоль прямой, соединяющей центры шаров (рис.1) (линия центров).
m1 m2
1 2
Рис.1 Найдем скорости шаров после удара по заданным скоростям до удара
1 |
и 2 и известным массам шаров m1 и m2 . |
Абсолютно неупругий удар
Закон сохранения импульса имеет вид:
4
m1 1 m2 2 (m1 m2) , |
(1) |
где - общая скорость шаров после удара.
Отсюда |
|
|
m |
m |
(2) |
|
1 1 |
2 2 |
|||
|
|
m1 m2
Законсохраненияэнергии записываетсяввиде:
1 |
|
2 |
1 |
|
|
|
2 |
1 |
|
|
|
|
2 |
|
|
|||||
|
|
m1 1 |
|
|
|
m2 2 |
|
|
(m1 m2 ) |
|
Q |
(3) |
||||||||
|
2 |
2 |
2 |
|
||||||||||||||||
где Q - часть энергии, которая перешла во внутреннюю при ударе. |
||||||||||||||||||||
Подставив значение из (2) в (3), найдем |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
m m |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Q |
2 |
|
|
1 2 |
|
|
)2 |
|
|
|
|||||||
|
|
|
|
|
|
( |
|
2 |
|
|
(4) |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
m |
m |
1 |
|
|
|
|
||||||||
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||
где mэф |
m1m2 |
|
называется эффективной (приведенной) массой |
|||||||||||||||||
m m |
||||||||||||||||||||
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
системы.
Можно показать, что в системе центра масс начало координат совпадает с центром масс (инерции), задача о центральном соударении двух шаров сводится к задаче о движении одного тела с эффективной массой.
Абсолютно упругий удар
На основании закона сохранения импульса и закона сохранения энергии можно написать:
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
m1 1 |
m2 2 m1u1 |
m2u2 |
|
(5) |
|||||||||
1 |
2 |
|
1 |
2 |
|
1 |
|
2 |
|
1 |
|
2 |
|
|
|
m1 1 |
|
|
m2 2 |
|
|
m1u1 |
|
|
|
m2u2 |
(6) |
||
2 |
2 |
2 |
2 |
|||||||||||
где u1 и u2 - скорости шаров 1 и 2 после удара. Представим (5) в виде
5
|
|
|
|
|
|
) m2 |
|
|
|
|
а (6) в виде |
m1( 1 |
u1 |
(u2 |
2) |
(7) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8) |
|||||||
m1( 1 |
u1 |
)( 1 |
u1 |
) m2 (u2 |
2 )( 2 |
u2 ) |
||||
После центрального удара векторы скоростей будут также лежать на линии центров шаров, так как силы взаимодействия во время удара, вследствие симметрии, будут направлены по этой же прямой. Следовательно, все векторы в (7) и (8) будут коллинеарны. Поэтому из(7) и (8) получим
|
|
|
|
|
|
|
|
1 u1 |
u |
2 2 |
(9) |
||
Умножая (9) на m2 |
и вычитая результат из (7), получим скорость |
|||||
первого шара после удара |
|
|
|
|||
u |
|
2m2 2 (m1 m2) 1 |
(10) |
|||
|
||||||
1 |
|
|
|
m1 |
m2 |
|
|
|
|
|
|
||
Умножая (9) на m1 и складывая результат с (7), получим скорость второго шара после удара
u2 |
|
2m1 1 (m2 m1) 2 |
(11) |
|
m1 m2 |
||||
|
|
|
Рассмотрим частный случай, когда массы соударяющихся шаров равныm1=m2=m.
Подставив это условие в (10) и (11), получим
|
|
|
|
u1 |
2 |
и u2 |
1 , |
т.е. шары при соударении обмениваются скоростями. В частности, если один из шаров, например, второй покоился до соударения, то после удара он движется с такой же скоростью, какую имел вначале первый шар, первый же шар после удара остановится.
В данной работе проверяется закон сохранения импульса. До столкновения первый шар имел импульс:
p1 m1 1 |
(12) |
где m1 - масса ударяющего шара (вместе с массой нижнего подвеса),
1 - скорость ударяющего шара.
Скорость 1 находим, используя закон сохранения механической энергии шара. Если отвести шар 1 от положения равновесия на угол
6
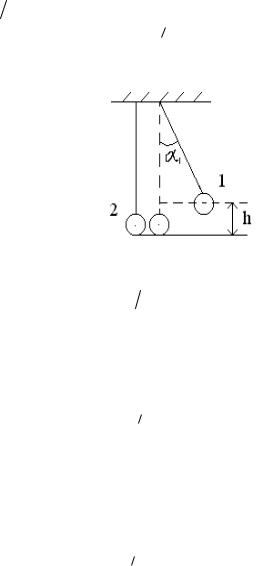
1, то он будет обладать запасом потенциальной энергии En m1gh. Если шар отпустить, то в момент соприкосновения с шаром 2 вся потенциальная энергия шара 1 превратится в кинетическую
2
Ek 1 2m1 1 . Отсюда получим
|
(2gh)1 2 |
|
1 |
(13) |
|
Рис.2. |
|
||||
Из рис.2 видно, что |
( h) cos 1, |
откуда |
||||
h 2 gsin2 |
1 |
|
|
(14) |
||
|
|
|
|
|||
|
2 |
|
|
|
||
Подставляя (14) |
в (13), получим: |
|
||||
|
|
|
1 |
|
|
|
1 |
2(g )1 2 sin |
|
|
(15) |
||
|
|
|
||||
|
2 |
|
|
|||
Если произошел абсолютно упругий удар, то полный импульс шаров после удара
|
|
|
|
p2 m1u1 |
m2u2 |
(16) |
|
Скорости u1и u2 определяются по формулам
u |
2(g )1 2 sin |
1 |
(17) |
|
|||
1 |
2 |
|
|
|
|
||
7

u2 |
2(g )1 2 sin |
2 |
(18) |
|
|||
|
2 |
|
|
где 1' и 2' - углы, на которые отклонились шары после удара.
Если произошел абсолютно неупругий удар, то полный импульс системы после удара
|
' (m m |
|
' |
|
p |
) |
|||
|
1 |
2 |
|
(19) |
здесь ' - общая скорость шаров после абсолютно неупругого удара
|
|
2(g )1 2 sin |
|
|
|
|
(20) |
||||
|
|||||
|
|
2 |
|||
Средняя сила соударения двух шаров
На основании второго закона Ньютона:
<F>Δt=ΔΚ , |
|
(21) |
где <F> - средняя сила удара, Δt - |
длительность |
удара, К - |
изменение импульса одного из соударяющихся шаров. Измерив среднее время соударения шаров Δt и определив из экспериментальных данных изменение импульса шара 2, можно определить из формулы (21) среднюю силу соударения двух шаров.
Восстановление скорости и энергии для случая удара шаров
Из закона сохранения импульса (второй шар неподвижен,2 = 0) имеем
|
|
|
|
m1 1 |
m1u1 |
m2u2 , |
(22) |
где m1 - масса правого шара,
8
m2 - масса левого шара,
u1 , u2 - скорости шаров после соударения,
1 - скорость правого шара до соударения.
Скорости шаров до и после удара можно определить по формулам (15), (17) и (18). В этих формулах l – расстояние от точки подвеса до центра тяжести шаров.
Коэффициент восстановления скорости можно определить по формуле:
|
|
|
|
|
КСк=| u2 - |
u1 |
|/| 2 |
- 1 | |
(23) |
Коэффициент восстановления энергии можно определить по
формуле:
Кэ = [m1 · sin2 (α1'/2) + m2 · sin2 (α2'/2)] / m1 · sin2 (α1/2) (24)
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Общий вид установки представлен на рис.3. Установка включает в свой состав: основание, вертикальную стойку, верхний кронштейн, корпус, электромагнит, нити подвески металлических шаров, провода для обеспечения электрического контакта шаров с клеммами. Установка работает от блока электронного.
Основание снабжено тремя регулируемыми опорами и зажимом для фиксации вертикальной стойки.
На верхнем кронштейне, предназначенном для подвески шаров, расположены узлы регулировки, обеспечивающие прямой центральный удар шаров, и клеммы.
На нижнем кронштейне закреплена шкала угловых перемещений. Справа на корпусе находится электромагнит, который предназначен для фиксации исходногоположения одногоиз шаров.
Металлические шары выполнены попарно из алюминия, латуни и стали.
9

Рис.3.
10
