
Контр. Раб. по математике
.docОбъяснительная записка
Данные методические указания содержат варианты контрольной работы по разделам «Аналитическая геометрия» и «Линейная алгебра» и образцы решения задач
Работа составлена в 25 вариантах. Номер варианта совпадает с номером фамилии студента в списке группы.
При выполнении контрольной работы необходимо делать ссылки на соответствующие теоремы и формулы. Это позволит глубже изучить материал и облегчит студенту защиту контрольной работы.
Варианты контрольной работы
-
Даны два вектора
 и
и
 .
Найти угол между ними и площадь
треугольника построенного на этих
векторах как на составляющих. Определить
высоту треугольника, опущенную на
сторону
.
Найти угол между ними и площадь
треугольника построенного на этих
векторах как на составляющих. Определить
высоту треугольника, опущенную на
сторону
 .
Будут ли коллинеарны векторы
.
Будут ли коллинеарны векторы
 и
и
 ?
?
-
Доказать, что векторы
 некомпланарны. Найти разложение
некомпланарны. Найти разложение
 по
векторам
по
векторам
 .
.
-
Определить при каком значении параметра k векторы
 и
и
 ортогональны.
ортогональны.
-
Даны вершины тетраэдра ABCD. Найти высоту опущенную из вершины D. Определить угол, образуемый ребром AD с плоскостью основания.
-
Даны координаты вершин треугольника ABC. Составить уравнения сторон треугольника, уравнение медианы и высоты, проведенных из вершины A. Найти длину высоты, опущенной из вершины B. Сделать чертёж в плоскости xOy.
-
Определить тип кривых второго порядка и их основные параметры. Сделать чертёж.
-
 ;
;  ;
;
 ;
;
 .
. -
 ;
;  ;
;
 ;
;
 .
. -
 ;
;  ;
;
 ;
;
 .
. -
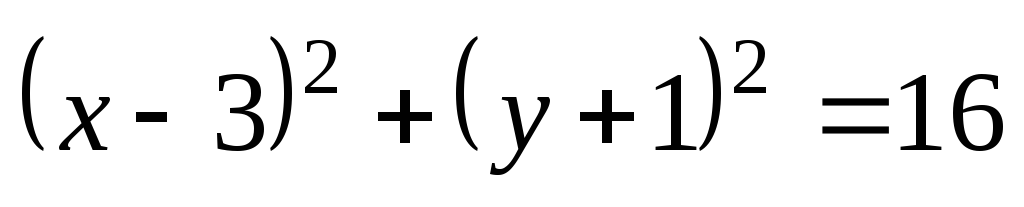 ;
;  ;
;
 ;
;
 .
. -
 ;
;  ;
;
 ;
;
 .
. -
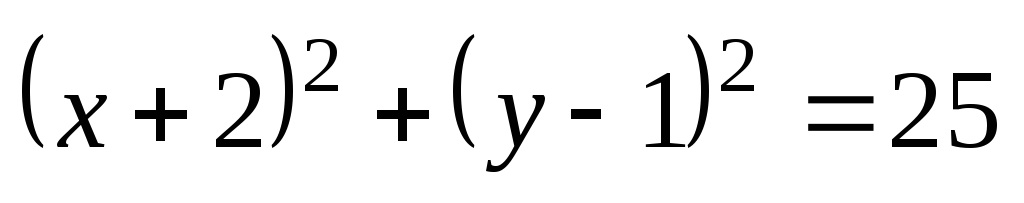 ;
;  ;
;
 ;
;
 .
. -
 ;
;  ;
;
 ;
;
 .
. -
 ;
;  ;
;
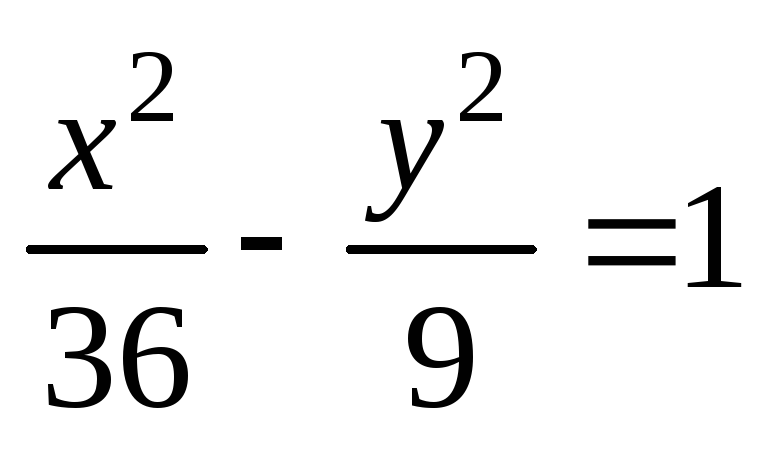 ;
;
 .
. -
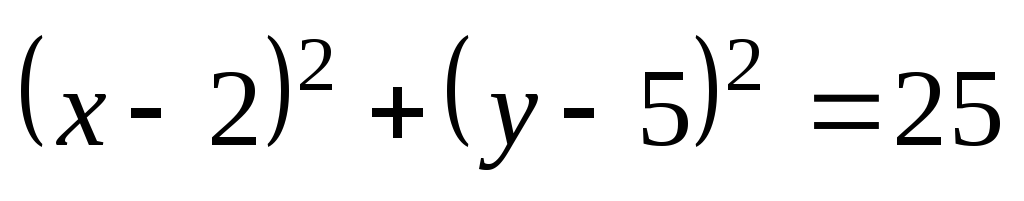 ;
;  ;
;
 ;
;
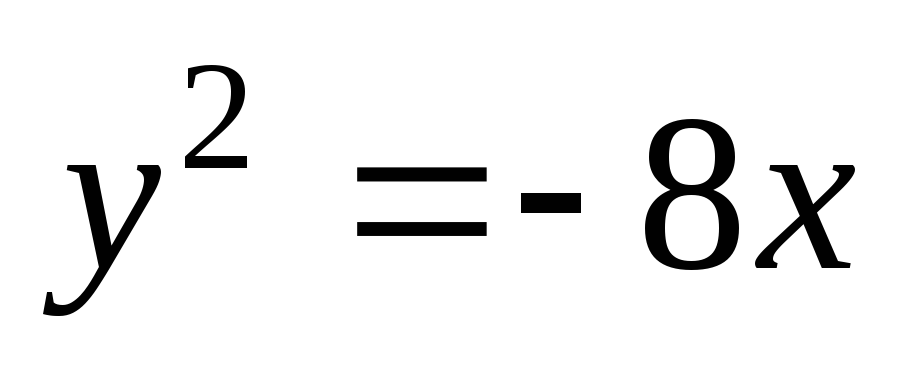 .
. -
 ;
;  ;
;
 ;
;
 .
. -
 ;
;  ;
;
 ;
;
 .
. -
 ;
;  ;
;
 ;
;
 .
. -
 ;
;  ;
;  ;
;
 .
. -
 ;
;  ;
;
 ;
;
 .
. -
 ;
;  ;
;  ;
;
 .
. -
 ;
;  ;
;
 ;
;
 .
. -
 ;
;  ;
;
 ;
;  .
. -
 ;
;  ;
;
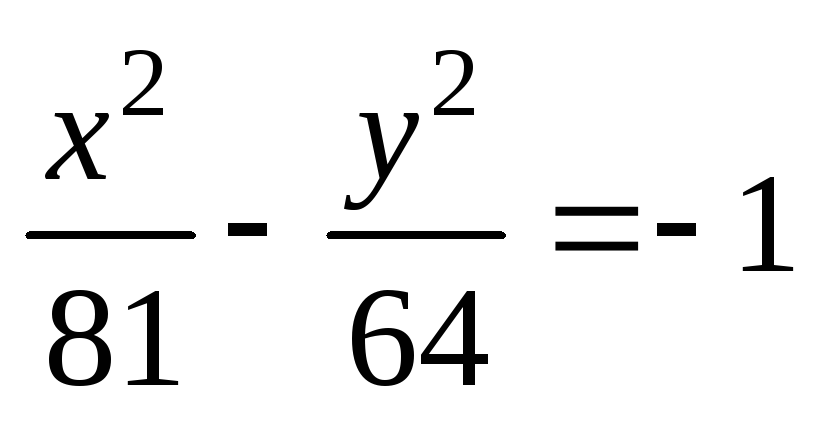 ;
;  .
. -
 ;
;  ;
;
 ;
;  .
. -
 ;
;  ;
;
 ;
;  .
. -
 ;
;  ;
;
 ;
;  .
. -
 ;
;  ;
;
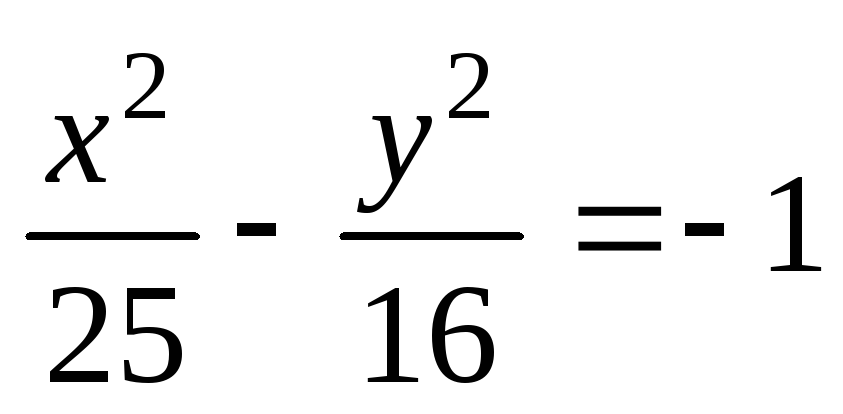 ;
;  .
. -
 ;
; 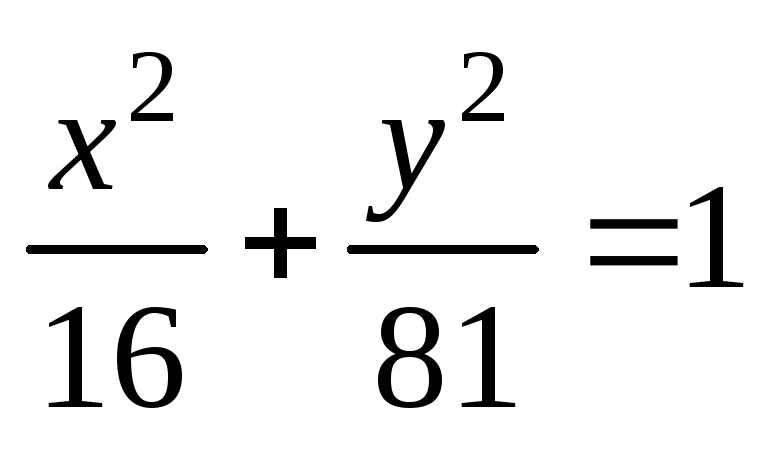 ;
;
 ;
;
 .
. -
 ;
;  ;
;
 ;
;  .
. -
 ;
; 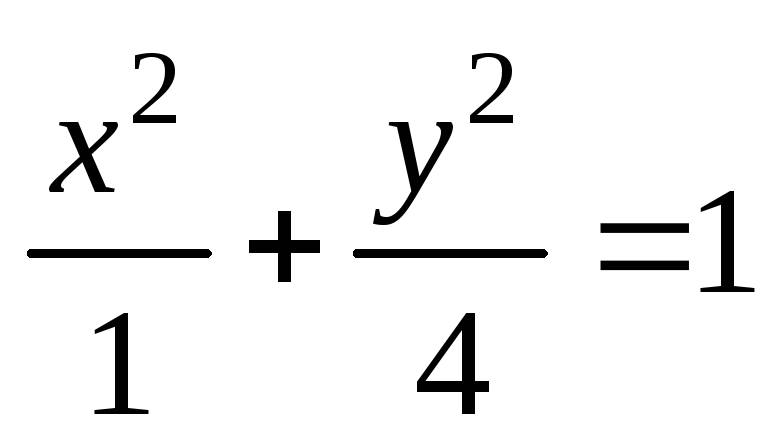 ;
;
 ;
;  .
.
-
Найти угол между плоскостями. Написать каноническое уравнение линии пересечения плоскостей.
-
Найти точку M пересечения прямой l и плоскости π. Написать уравнение прямой, проходящей через точку A: а) параллельно данной прямой (l1); б) перпендикулярно данной плоскости (l2 ). Найти точку B, симметричную данной точке A относительно данной плоскости.
-
l:
 ; π
:
; π
: ; A(2,
1, 1
).
; A(2,
1, 1
). -
l:
 ; π
:
; π
: ;
A(
4,
-1, 0).
;
A(
4,
-1, 0). -
l:
 ; π
:
; π
: ;
A(
1,
2, -1).
;
A(
1,
2, -1). -
l:
 ; π
:
; π
: ;
A(0,
1,
-2).
;
A(0,
1,
-2). -
l:
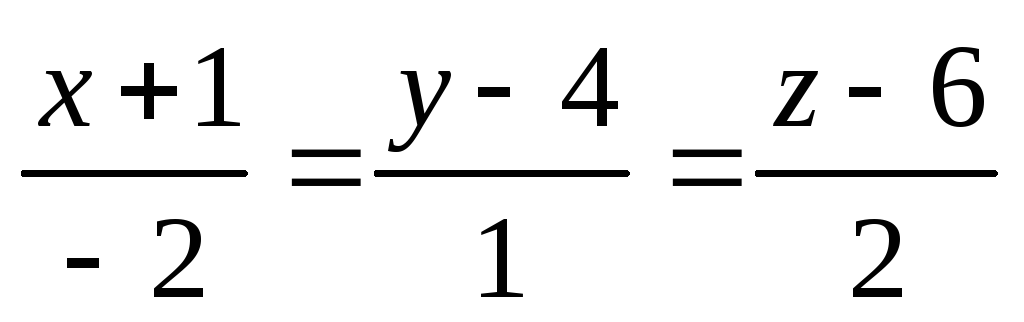 ; π
:
; π
: ; A(7,
4, 1 ).
; A(7,
4, 1 ). -
l:
 ;
π
:
;
π
: ;
A(2, -4, 1 ).
;
A(2, -4, 1 ). -
l:
 ; π:
; π: ;
A(0,
5, 7
).
;
A(0,
5, 7
). -
l:
 ; π
:
; π
: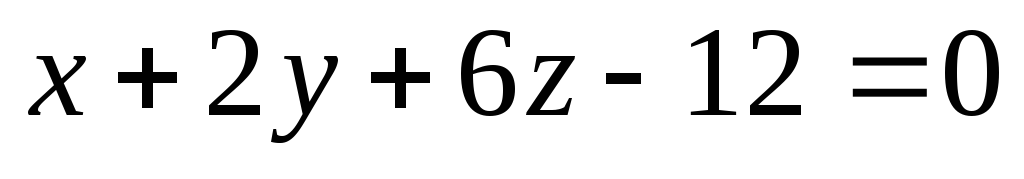 ;
A( 1,
-1, 5 ).
;
A( 1,
-1, 5 ). -
l:
 ; π
:
; π
: ;
A(2,
0, -1
).
;
A(2,
0, -1
). -
l:
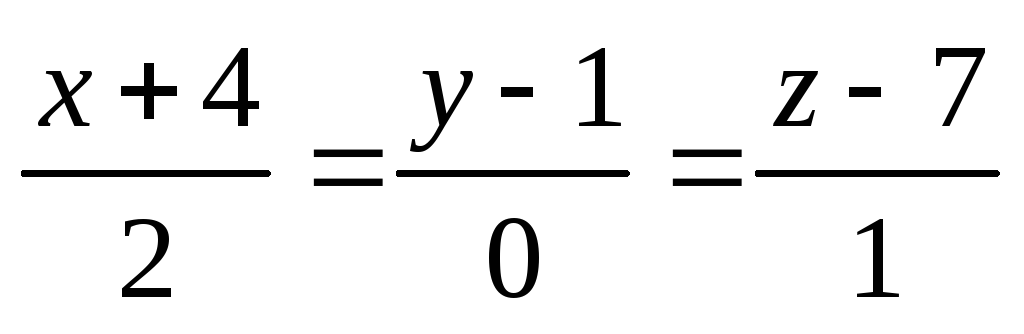 ; π
:
; π
: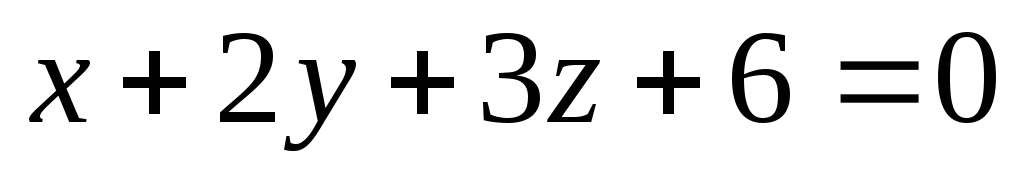 ;
A(-1,
-1, 2
).
;
A(-1,
-1, 2
). -
l:
 ; π
:
; π
: ;
A(1,
1, 1
).
;
A(1,
1, 1
). -
l:
 ; π
:
; π
: ;
A(9,
7, 0
).
;
A(9,
7, 0
). -
l:
 ; π
:
; π
: ;
A(0,
5, 8
).
;
A(0,
5, 8
). -
l:
 π
:
π
: A( 0,
2, 0).
A( 0,
2, 0). -
l:
 π
:
π
: A(1,
2, 0
).
A(1,
2, 0
). -
l:
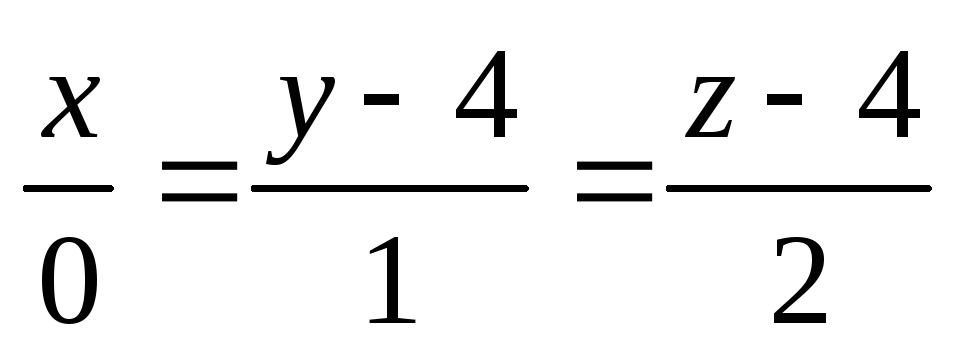 π
:
π
: A( 1,
7, 6).
A( 1,
7, 6). -
l:
 π
:
π
: A( 2,
3, -1).
A( 2,
3, -1). -
l:
 π
:
π
: A(
1,
2, 1).
A(
1,
2, 1). -
l:
 π
:
π
: A(
1,
2, -4).
A(
1,
2, -4). -
l:
 π
:
π
: A(1,
1, 1
).
A(1,
1, 1
). -
l:
 π
:
π
: A(1,
-1, 7
).
A(1,
-1, 7
). -
l:
 π
:
π
: A( 0,
8, 3).
A( 0,
8, 3). -
l:
 π
:
π
: A(
2,
2, 0).
A(
2,
2, 0). -
l:
 π
:
π
: A(
1, -1, 2).
A(
1, -1, 2). -
l:
 π
:
π
: A(1,
2, -3 ).
A(1,
2, -3 ).
Теоретический материал.
Векторы. Основные операции над векторами
Вектор – направленный отрезок.
Вектор характеризуется длиной и направлением.
Длина вектора – расстояние между началом и концом отрезка.
Начало вектора не фиксируется, его можно приложить к любой точке пространства.
Два вектора равны, если они одной длины и одинаково направлены.
Два вектора называются коллинеарными, если они лежат на параллельных прямых.
Коллинеарные
векторы делятся на сонаправленные
и противоположно
направленные:
![]() – сонаправленные,
– сонаправленные,
![]() - противоположно направленные.
- противоположно направленные.
Векторы называются компланарными, если они лежат на параллельных плоскостях или в одной плоскости.
На трех некомпланарных векторах, как на составляющих, можно построить параллелепипед.
Д
 ействие
с векторами: 1.
Сложение:
ействие
с векторами: 1.
Сложение:
