Розділ 1. Гармонічні коливання і хвилі Основні формули
1. Зміщення, швидкість і прискорення матеріальної точки при гармонічних коливаннях визначаються рівняннями:
х = А cos ( t + 0),
υ = - A sin (t + 0),
a = - A 2cos (t + 0) = - 2 x,
де А - амплітуда коливань;
- циклічна частота;
0 - початкова фаза коливань.
2. Зв’язок циклічної частоти з періодом коливань Т і частотою :
=
= 2
.
3. Сила, яка діє на тіло при вільних гармонічних коливаннях (квазіупружна сила):
F = ma = - m 2 x = - k x,
де k = m2 - коефіцієнт квазіупружної сили, який вимірюється силою, що визиває зміщення х = 1.
4. Кінетична, потенціальна і повна енергії гармонічних коливань матеріальної точки:
,
,
.
5. Диференціальні рівняння малих коливань:
а) математичний маятник
+
x = 0, де
,звідки
T = 2
;
б) пружинний маятник
+
x
= 0, де
, звідкиТ
= 2
;
в) фізичний маятник
+
x = 0, де
, звідкиT
= 2
,
де І - момент інерції маятника відносно осі коливань;
l - відстань від осі коливань до центра мас маятника;
-
приведена довжина.
При відсутності опору середовища циклічна частота коливань називається власною циклічною частотою і позначається через 0.
6. При додаванні двох однаково направлених гармонічних коливань однакового періоду одержуємо гармонічне коливання того ж періоду, амплітуда якого А і початкова фаза 0 визначаються рівняннями:
,
tq
0
=
,
де А1 і А2 - амплітуди коливань, що складаються;
1 і 2 - початкові фази цих коливань.
7. При додаванні двох однаково направлених гармонічних коливань однакової амплітуди і близьких частот (1 2) одержуємо биття, яке описується рівнянням:
x
=
cos
,
де
- амплітуда биття.
Періодичність зміни амплітуди визначається періодичністю зміни модуля косинуса, тому період биття дорівнює:
Tб
=
, звідки Tб
=
.
8. При додаванні двох взаємно перпендикулярних гармонічних коливань з однаковою частотою в напрямі координатних осей х і у матимемо рівняння траєкторії результуючого руху матеріальної точки:
cos(2
- 1)
= sin2
(2
- 1),
де А1 і А2 - амплітуди коливань, що додаються;
2 - 1 - різниця фаз цих коливань.
9. Диференціальне рівняння загасаючих коливань :
0,
або
де
=
- коефіцієнт загасання;
r - коефіцієнт опору середовища;
-
власна циклічна частота коливань.
10. Загальний розв’язок диференціального рівняння для загасаючих коливань має вигляд:
x = A0e-t cos (t + ),
де А0е-t - амплітуда загасаючих коливань;
- циклічна частота загасаючих коливань.
11. Швидкість зменшення амплітуди загасаючих коливань характеризують логарифмічним декрементом загасання
δ=
ln
,
де δ - логарифмічний декремент загасання;
- коефіцієнт загасання;
Т - період загасаючих коливань.
12. Циклічна частота загасаючих коливань
=
, або
=
.
13. Період загасаючих коливань:
T
=
, або Т =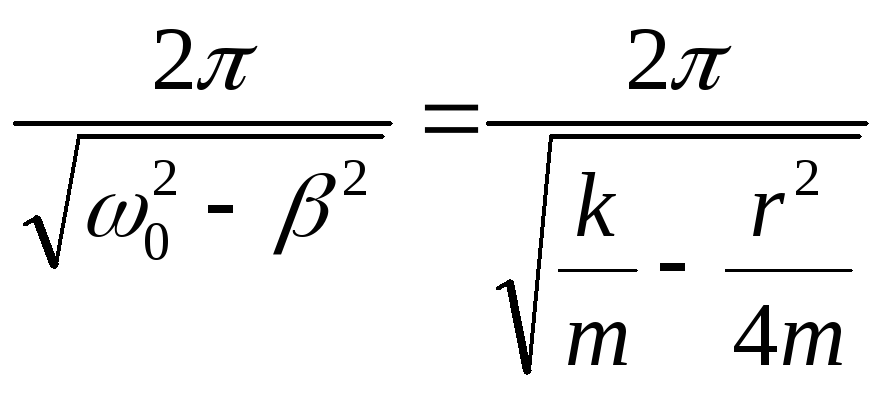
.
14. Добротність коливальних систем
=
2
, або
=
,
де Wt - повна енергія, яку має коливальна система на момент часу t;
W(t=T) - втрати енергії коливальної системи за один період; δ - логарифмічний декремент загасання;
- коефіцієнт загасання;
0 - власна циклічна частота коливань;
Т - період загасаючих коливань (при малих загасаннях Т Т0).
15. Диференціальне рівняння вимушених коливань
,
або
де F0 - вимушувана сила;
- циклічна частота вимушених коливань.
16. Загальний розв’язок диференціального рівняння вимушених коливань, які протягом певного часу встановлюються під дією вимушуваної сили має вигляд:
x = A cos (t + )
де А - амплітуда вимушених коливань;
- зсув за фазою вимушених коливань і вимушуваної сили.
17. Амплітуда вимушених коливань
A
=
,
де
f0
=
;
0 - власна частота коливань системи;
- циклічна частота вимушуваної сили.
18. Зсув фази вимушених коливань:
tg
= -
.
19. Резонансна частота і резонансна амплітуда:
рез
=
;
Арез
=
.