
- •С.Г.Авдєєв, т.І.Бабюк
- •1.1.Кінематика руху матеріальної точки. Системи координат. Переміщення і швидкість руху. Пройдений шлях. Середні значення кінематичних величин.
- •1.2. Рух точки по колу. Кутова швидкість і кутове прискорення.
- •1.3. Тангенціальне і нормальне прискорення. Зв’язок між кінематичними величинами криволінійного руху.
- •1.1. Кінематика руху матеріальної точки. Системи координат.
- •1.2. Рух точки по колу. Кутова швидкість і кутове прискорення
- •1.3. Тангенціальне й нормальне прискорення. Зв’язок між кінематичними величинами криволінійного руху
- •Лекція 2
- •2.2. Другий закон Ньютона. Рівняння руху точки
- •2.3. Третій закон Ньютона. Закон збереження імпульсу
- •Лекція 3
- •3.2. Консервативні й неконсервативні сили. Потенціальна енергія. Зв’язок роботи й потенціальної енергії
- •Знайдемо роботу переміщення матеріальної точки з положення м1 в положення м2. Для цього спочатку знайдемо роботу переміщення точки (тіла) з точки “м1” в точку “о” і з точки “м2” в точку “о”.
- •,.(3.2.4)
- •3.3.Сила й потенціальна енергія. Поняття градієнта
- •3.4. Закон збереження й перетворення механічної енергії
- •Лекція 4
- •4.2. Моменти інерції найпростіших тіл: диск, стержень, куля.
- •4.4. Закон збереження моменту імпульсу і його використання. Гіроскопи. Гіроскопічний ефект
- •Лекція 5
- •5.2. Наслідки перетворення координат Лоренца.
- •5.3. Зв’язок маси і енергії
- •Лекція 6
- •6.2. Електричне поле і його напруженість. Принцип суперпозиції полів. Поле точкового заряду
- •6.3. Теорема Гаусса і її використання
- •З рисунка видно, що
- •За теоремою Гаусса
- •7.2. Потенціал електростатичного поля. Різниця потенціалів. Принцип суперпозиції
- •7.3. Зв’язок між потенціалом і напруженістю електростатич-ного поля. Приклади розрахунку полів
- •Рис 7.5
- •Лекція 8
- •8.2. Електроємність окремого провідника. Конденсатори. Ємність конденсаторів різної форми
- •8.3. Енергія взаємодії електричних зарядів. Енергія окремого провідника і конденсатора
- •8.4. Енергія електростатичного поля. Густина енергії електро-статичного поля
- •Лекція 9
- •9.2. Вектор електричного зміщення. Теорема Гаусса для поля в
- •Постійний електричний струм
- •Струм і існує у зовнішній ділянці кола і створюється полем . Струміснує у джерелі і створюється полем сторонніх сил.
- •10.2. Закон Джоуля-Ленца в інтегральній формі. Опір провідників. Потужність струму
- •10.3. Закони Ома для ділянки кола, неоднорідної ділянки кола й замкнутого кола. Правила Кірхгофа
- •10.4. Закони Ома й Джоуля-Ленца в диференціальній формі. Густина електричного струму в провіднику
- •Лекція 11
- •11.2. Закон Біо-Савара-Лапласа та його використання у найпростіших випадках
- •Лекція 12
- •12.2. Ефект Холла. Магнітогазодинамічний генератор та його використання
- •12.3. Явище електромагнітної індукції
- •12.4. Самоіндукція. Індуктивність. Е.Р.С. Самоіндукції
- •Лекція 13
- •13.2. Магнітний потік. Теорема Гаусса для магнітного поля
- •13.3. Робота переміщення провідника із струмом і контуру із струмом у магнітному полі
- •13.4. Енергія магнітного поля
- •Лекція 14
- •Розглянемо цей випадок трохи детальніше. Скористаємось другим законом Ньютона
- •14.2. Магнітна сприйнятливість і проникність
- •14.3. Циркуляція намагнічування. Вектор напруженості магнітного поля
- •14.4. Феромагнетики та їх основні властивості
- •Програма першої частини
- •Плани практичних занять
- •Графік виконання лабораторних робіт
- •Контрольні запитання для захисту лабораторних робіт
- •Тренувальні варіанти контрольної роботи 1 Варіант 1
- •Варіант 2
- •Варіант 3
- •Колоквіум 1
- •З м і с т
4.4. Закон збереження моменту імпульсу і його використання. Гіроскопи. Гіроскопічний ефект
Скористаємось основним рівнянням динаміки обертального руху (4.3.6)
![]() (4.4.1)
(4.4.1)
Якщо
система замкнута, то будь-які зовнішні
сили будуть відсутні. Це означає, що
![]() .
Тому для замкнутої системи виконується
рівність
.
Тому для замкнутої системи виконується
рівність
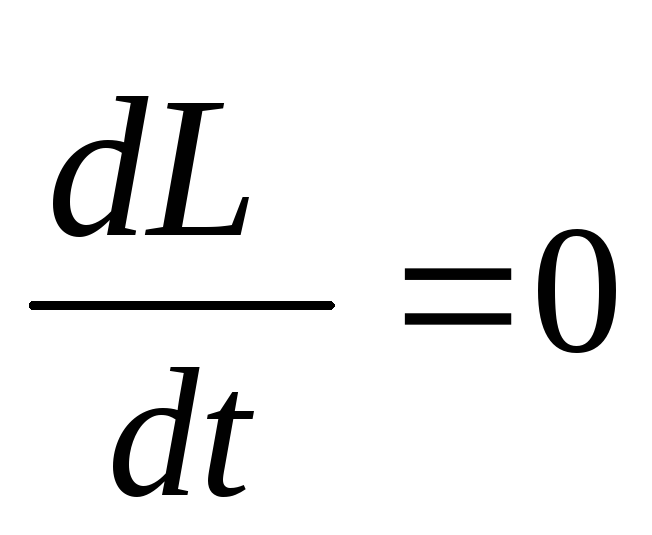 .
(4.4.2)
.
(4.4.2)
Рівність (4.4.2) має місце лише в одному випадку: коли результуючий момент імпульсу дорівнює сталій величині, тобто
![]() .
(4.4.3)
.
(4.4.3)
В будь-якій замкнутій системі сумарний момент імпульсу всіх тіл цієї системи з часом не змінюється. Це і є формулювання закону збереження моменту імпульсу. Закон збереження моменту імпульсу має досить широке використання.
Оскільки
![]() ,
(4.4.4)
,
(4.4.4)
то зміна моменту інерції Іі приводить до відповідної зміни кутової швидкості. Приклади використання закону збереження моменту імпульсу мають місце в техніці (наприклад регулятор Уатта), в спорті (фігурне катання) тощо.
Масивні симетричні тіла, які обертаються з великою кутовою швидкістю, називаються гіроскопами.
Якщо до гіроскопа, який здійснює обертальний рух прикласти дві сили, які намагаються повернути його навколо осі, перпендикулярної до осі обертання, то гіроскоп повернеться відносно третьої осі, перпендикулярної до перших двох осей. Цю властивість гіроскопа називають гіроскопічним ефектом (рис.4.9).
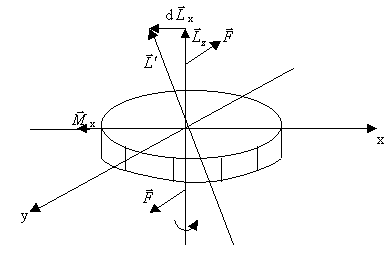
Рис.4.9
Дія
пари сил
![]() призводить
до повертання гіроскопа відносно осіх.
Напрям моменту сил
призводить
до повертання гіроскопа відносно осіх.
Напрям моменту сил
![]() x
збігається
з віссю х.
x
збігається
з віссю х.
У
відповідності з основним рівнянням
динаміки обертального руху виникає
додатковий момент імпульсу
![]() ,
тобто
,
тобто
![]() .
.
Вісь
обертання гіроскопа z
повернеться і займе нове положення
вздовж рівнодійної векторів
![]() і
і![]() .
Це рівноцінно тому, що гіроскоп
повертається відносно осі
y.
.
Це рівноцінно тому, що гіроскоп
повертається відносно осі
y.
Сучасні гіроскопи широко використовуються у техніці. Обертаю-чись з кутовою швидкістю у сотні тисяч обертів за хвилину, гіроскопи допомагають прокладати курс різноманітним плавзасобам, стабілізують польоти ракет тощо.
Лекція 5
Елементи спеціальної теорії відносності
5.1. Постулати спеціальної теорії відносності. Перетворення координат Лоренца.
5.2. Наслідки перетворення координат Лоренца. Закон складання швидкостей.
5.3. Зв’язок маси й енергії.
5.1. Постулати спеціальної теорії відносності
Перетворення координат Лоренца
В класичній механіці Ньютона для тіл, які рухаються з швидкостями, набагато меншими за швидкість світла (v<<с), виконується механічний принцип відносності Галілея.
Суть класичного принципу відносності полягає в тому, що закони динаміки однакові для всіх інерціальних систем відліку.
Розглянемо дві інерціальні системи координат відліку (рис.5.1).

Рис. 5.1.
Інерціальну
систему з координатами x,
y,
zбудемо вважати нерухомою. Система,
координати якої
![]() ,
,![]() ,
,![]() рухається відносно нерухомої системи
з сталою швидкістюu.
рухається відносно нерухомої системи
з сталою швидкістюu.
В довільний момент часу t
![]() =
x - ut,
=
x - ut,
![]() =y,
=y,
![]() =z,
=z,
![]() =
t. (5.1.1)
=
t. (5.1.1)
Ці перетворення координат називаються перетвореннями Галілея.
Диференціюємо ці перетворення за часом і знайдемо закон складання швидкостей у класичній механіці:
![]()
![]()
![]() . (5.1.2)
. (5.1.2)
де
![]() -
швидкість руху матеріальної точки в
напрямі осіxвідносно
штрихованої системи координат;
-
швидкість руху матеріальної точки в
напрямі осіxвідносно
штрихованої системи координат;![]() - швидкість руху матеріальної точки в
напрямі осіхвідносно нерухомої
системи координат;u– швидкість руху штрихованої системи
відносно не штрихованої системи.
- швидкість руху матеріальної точки в
напрямі осіхвідносно нерухомої
системи координат;u– швидкість руху штрихованої системи
відносно не штрихованої системи.
У векторній формі класичний закон складання швидкостей матиме вигляд:
![]() .
(5.1.3)
.
(5.1.3)
Диференціюємо за часом вираз (5.1.3), одержимо:
![]() ,
або
,
або![]() .
(5.1.4)
.
(5.1.4)
Прискорення матеріальної точки інваріантне відносно перетворень координат Галілея. Можна також стверджувати, що сили теж є інваріантними величинами відносно перетворень координат Галілея
![]() .
(5.1.5)
.
(5.1.5)
Висновок:У будь-яких інерційних системах відліку всі механічні явища за однакових умов є інваріантні (однакові).
Цей висновок носить назву механічного принципу відносності.
У 1905 році видатний фізик ХХ сторіччя Альберт Ейнштейн, аналізуючи великий експериментальний матеріал, сформулював два постулати створеної ним спеціальної теорії відносності, суть яких така:
у будь-яких інерційних системах відліку всі фізичні явища за однакових умов відбуваються однаково;
швидкість світла у вакуумі не залежить від швидкості руху джерела світла.
З першого постулату Ейнштейна виходить, що за допомогою будь-яких фізичних дослідів, поставлених у замкнутій системі, неможливо виявити рухається ця система чи перебуває у стані спокою.
Другий постулат Ейнштейна суперечить класичному закону додавання швидкостей.
З постулатами спеціальної теорії відносності перебувають у відповідності не перетворення координат Галілея, а дещо складніші перетворення, які називаються перетвореннями координат Лоренца.
Нехай штрихована система рухається відносно не штрихованої системи координат з сталою швидкістю , при чомуc. Нехай швидкістьнаправлена уздовж осі ОХ. Тоді релятивістські перетворення координат Лоренца будуть мати вигляд:

![]() =
=
![]() ;
;![]() =
=
![]() ;
;
 .
(5.1.6)
.
(5.1.6)
Координати штрихованої системи по відношенню до координат нештрихованої системи:
 ;
;
![]() =
=
![]() ;
;![]() =
=
![]() ;
; .
(5.1.7)
.
(5.1.7)
У випадку, коли v<<c, перетворення координат Лоренца переходять у класичні перетворення Галілея:
х=![]() +t,
+t,
![]()
![]() ,
,
![]() ,
,![]() ;
;
або
![]() =x
-
t,
=x
-
t,
![]()
![]() ,
,
![]() ,
,![]() .(5.1.8)
.(5.1.8)
Класична механіка придатна для розгляду таких рухів, швидкості яких, порівняно з швидкістю світла, досить малі.
Механіка, яка розглядає рух тіл з швидкостями, близькими до швидкості світла, називається релятивістською механікою.
