9.2.2 Поверхні з двома напрямними (Поверхні Каталана)

Каталан – бельгійський математик, який досліджував властивості цих поверхонь.

Ці поверхні утворюються рухом прямої лінії, яка для всіх своїх положень зберігає паралельність деякій заданій площині (площина паралелелізма) та перетинає напрямні. До них відносять: циліндроїд, параболоїд, коноїд.

1. Гіперболічний параболоїд (коса площина) – використовується в інженерно-будівній практиці при формуванні поверхонь укосів та насипів (рис. 68 ).

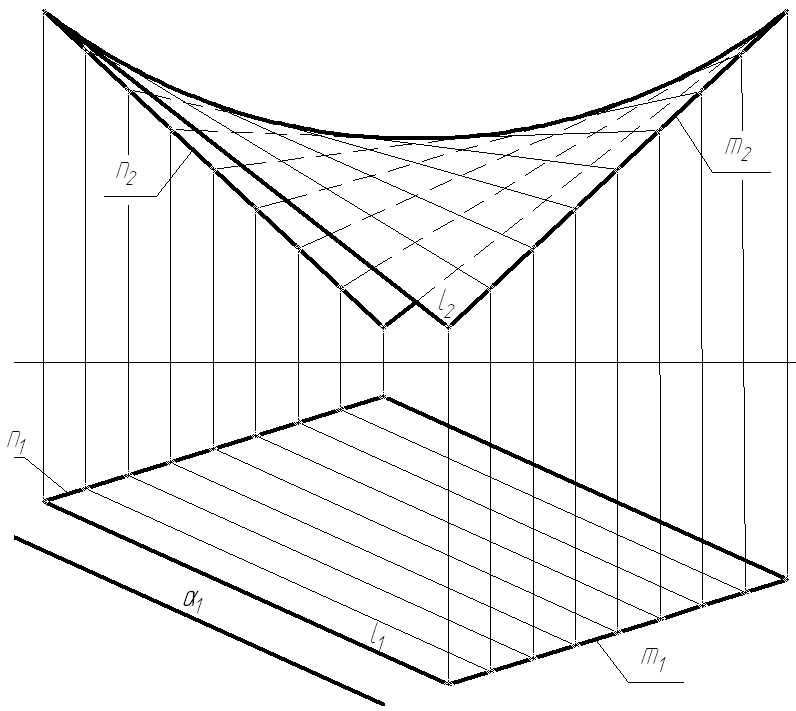
Рисунок 68 – Гіперболічний параболоїд

2. Коноїд – поверхня використовується в гідротехнічному будівництві для формування будівництва поверхні підвалин мостових опор (рис. 69).

Задача: Відомо, що т. А та В належать поверхні коноїда (рис. 69), але на кресленні задані лише їх проекції – А₁ та В₂. Побудувати відсутні проекції – А₂ та В₁.

Пояснення до побудов проекцій точок А₂ та В₁.

1. Із двох проекцій більш просто будується проекція т. В – В₁. Проводять через В₂ твірну l, паралельну α₂. Визначають перетин твірної l^і з напрямними m та n. Знаходять відсутню проекцію твірної l^і, куди на неї проекціюють точку В.

Рисунок 69 – Коноїд

2. Відсутню проекцію точки А (А₂) будують за рахунок введення допоміжної січної площини β (β┴П₁).

Ця площина перетинає поверхню коноїда по кривій а, на яку і проекціюємо відсутню проекцію точки А.

3. Циліндроїд має застосування у повітроводах великих діаметрів (рис. 70).

а) циліндроїд б) повітровід, поверхня якого є циліндроїдом

Рисунок 70 - Циліндроїд та його використання

Загальний визначник цих поверхонь:

Ø ( l, m, n, α),

де

l –твірна; l∩ m, n;

m, n –напрямні; lװα,

α– площина паралелізму. α – займає певне положення.

Нижче ознайомтесь з геометричною та алгоритмічною частинами визначників поверхонь, що показані, відповідно, на рис. 68 – 70.

1 Гіперболічний параболоїд:

m ,n – напрямні,прямі; lװα;

l – твірна; l∩m, n;

α – площина паралелізму. α П₁.

2 Коноїд:

m – напрямна, пряма; lװα ;

n – напрямна, крива; l∩m,n;

l – твірна; αװ П₁.

 – площина паралелізму.

3 Циліндроїд:

l – твірна; l׀׀α;

ГЧ m,n – напрямні, криві; l∩ m,n;

α – площина паралелізму. α П₁.

Отже, якщо слід побудувати одну із поверхонь Каталана, то необхідною умовою є задання геометричної частини визначника будь-якої із цих поверхонь та положення площини паралелелізму. Відсутні проекції точок, що належать цим поверхням, можна будувати :

а) за допомогою проекції твірної, використовуючи алгоритмічну частину визначника поверхні;

б) за допомогою січної площини (якщо для заданої проекції точки неможливо застосувати алгоритмічну частину визначника), яка перетинає твірні, що знаходяться поблизу заданої проекції точки.