Алгоритм визначення проекцій точок на поверхнях обертання

При визначенні проекцій точок слід пам’ятати, що деякі із них можуть бути визначені безпосередньо, оскільки знаходяться на характерних (обрисових) лініях цих поверхонь (екваторі, горлі, головному меридіані).

1. Поверхні обертання:

1.1 з криволінійною твірною;

а) проекції точок визначають тільки за допомогою паралелей;

б) через проекцію точки проводять паралель, яка перпендикулярна до осі обертання;

в) визначають радіус паралелі (від осі обертання вздовж паралелі до обрисового меридіана для однієї проекції або від сліду осі обертання до проекції точки – для другої проекції);

г) за характерними лініями (екватор, обрисовий меридіан) визначають видимість проекцій точок.

1.2 з прямолінійною твірною:

а) проекції точок можна визначити з допомогою паралелей або твірних;

б) паралелі, їх радіуси визначають аналогічно попередньому алгоритму;

в) твірні проводять, використовуючи алгоритм утворення поверхні.

9.2 Поверхні переносу

Поверхні переносу можна одержати поступальним рухом плоскої кривої, причому лінії, які утворюють поверхню, весь час залишаються паралельними між собою (рис. 64).

Ø (а, в) – загальний визначник поверхні,

д

АЧ

ГЧ

еа - твірна, крива; а׀׀а¹׀׀а²…׀׀аⁿ,

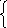
в - напрямна, пряма. а^і∩в.

Рисунок 64 – Утворення поверхні переносу

Для того, щоб перейти від задання поверхні елементів її визначником до задання поверхні каркасом, достатньо на напрямній прямій в з однаковим кроком відмітити ряд точок А, А′, А′′, … та через ці точки провести криві а¹,а², …, паралельні а.

Лінійчасті поверхні

До цих поверхонь відносяться поверхні: циліндр та конус обертання, конічна та циліндрична поверхні обертання загального положення, поверхні Каталана та торса (поверхня з ребром повертання). Ці поверхні утворюють переміщенням прямої - твірної l вздовж другої лінії (кривої чи прямої), яка називається напрямною.

9.2.1 Лінійчаті поверхні з однією напрямною

1. Циліндр загального положення – прямолінійна твірна l_l переміщається вздовж криволінійної напрямної m, причому всі твірні залишаються паралельними між собою (рис. 65).

Рисунок 65 - Утворення циліндричної поверхні

Запишемо загальний визначник цієї поверхні:

(l,m),

де

l – твірна, пряма лінія; l∩m;

m – пряма, крива, коло. l װl¹װl²װ…װlⁿ.

Межу видимості на П₁ утворюють твірні, які є дотичними до проекції кола. Проекції точок А та В будують, використовуючи алгоритмічну частину визначника, тобто через проекції т. А та В проводять твірні, які паралельні обрисовим циліндричної поверхні та перетинають напрямну m.

Через видиму проекцію т. А проводять видиму твірну, через невидиму проекцію т. В – невидиму. Т. С належить твірній, яка на П₁ є обрисовою.

2. Конус загального виду – прямолінійна твірнаl переміщається вздовж деякої напрямної m, яка проходить через одну i ту ж точку, яку називають вершиною S (рис. 66).

Рисунок 66 – Утворення конічної поверхні

Ø (l, m, S) – загальний визначник,

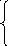
де

l – твірна, пряма; l l`l²…l = S;

ГЧ m – напрямна, крива, коло; l m.

S – вершина.

Проекції т. А та В знаходять, використовуючи алгоритмічну частину визначника. Проекції точок, що позначені в дужках, слід розуміти як ті, які невидимі. Т. С належить твірній, яка на П₂ є обрисовою.

3. Торс - поверхня з ребром повертання. (Tогs – витий, кручений).

Утворюється безперервним рухом прямолінійної твірної l, яка дотикається до деякої просторової криволінійної напрямної m (рис. 67).

Ø (l, m) – загальний визначник, де

l – твірна, пряма;

m – напрямна, просторова крива.

l^іº/ l,

l º m.

Читання знаків:

– мимобіжність

– дотик

Рисунок 67 – Побудова поверхні торса

Поверхні з однією напрямною відносяться до розгортуваних поверхонь.