AOM / Tannenbaum

без разделенной физической памяти возможно логическое разделение переменных, но сделать это несколько сложнее. Как мы видели выше, в системе Linda существует общее пространство кортежей, даже на мультикомпьютере, а в системе Осга поддерживаются разделенные объекты, общие с другими машинами. Существует и возможность разделения одного адресного пространства на мультикомпьютере, а также разбиение на страницы в сети. Процессы могут взаимодействовать между собой через общие переменные как в мультипроцессорах, так и в мультикомпьютерах.

Альтернативный подход — взаимодействие через передачу сообщений. В данной модели используются примитивы send и receive. Один процесс выполняет примитив send, называя другой процесс в качестве пункта назначения. Как только второй процесс совершает receive, сообщение копируется в адресное пространство получателя.

Существует множество вариантов передачи сообщений, но все они сводятся к применению двух примитивов send и recei ve. Они обычно реализуются как системные вызовы. Более подробно этот процесс мы рассмотрим ниже в этой главе.

Следующий вопрос при передаче сообщений — количество получателей. Самый простой случай — один отправитель и один получатель (двухточечная передача сообщений). Однако в некоторых случаях требуется отправить сообщение всем процессам (широковещание) или определенному набору процессов (муль-

тивещание).

Отметим, что в мультипроцессоре передачу сообщений легко реализовать путем простого копирования от отправителя к получателю. Таким образом, возможности физической памяти совместного использования (мультипроцессор/мультикомпьютер) и логической памяти совместного использования (взаимодействие через общие переменные/передача сообщений) никак не связаны между собой. Все четыре комбинации имеют смысл и могут быть реализованы. Они приведены в табл. 8.1.

Таблица8.1. Комбинации совместного использования физической и логической памяти

Базисные элементы синхронизации

Параллельные процессы должны не только взаимодействовать, но и синхронизировать свои действия. Если процессы используют общие переменные, нужно быть уверенным, что пока один процесс записывает что-либо в общую структуру данных, никакой другой процесс не считывает эту структуру. Другими словами, требуется некоторая форма взаимного исключения, чтобы несколько процессов не могли использовать одни и те же данные одновременно.

5 8 4 Глава 8. Архитектуры компьютеров параллельного действия

Существуют различные базисные элементы, которые можно использовать для взаимного исключения. Это семафоры, блокировки, мьютексы и критические секции. Все они позволяют процессу использовать какой-то ресурс (общую переменную, устройство ввода-вывода и т. п.), и при этом никакие другие процессы доступа к этому ресурсу не имеют. Если получено разрешение на доступ, процесс может использовать этот ресурс. Если второй процесс запрашивает разрешение, а первый все еще использует этот ресурс, доступ будет запрещен до тех пор, пока первый процесс не освободит ресурс.

Во многих параллельных программах существует и такой вид примитивов (базисных элементов), которые блокируют все процессы до тех пор, пока определенная фаза работы не завершится (см. рис. 8.11, б). Наиболее распространенным примитивом подобного рода является барьер. Когда процесс встречает барьер, он блокируется до тех пор, пока все процессы не наткнутся на барьер. Когда последний процесс встречает барьер, все процессы одновременно освобождаются и продолжают работу.

Классификация компьютеров параллельного действия

Многое можно сказать о программном обеспечении для параллельных компьютеров, но сейчас мы должны вернуться к основной теме данной главы — архитектуре компьютеров параллельного действия. Было предложено и построено множество различных видов параллельных компьютеров, поэтому хотелось бы узнать, можно ли их как-либо категоризировать. Это пытались сделать многие исследователи [39, 43, 148]. К сожалению, хорошей классификации компьютеров параллельного действия до сих пор не существует. Чаще всего используется классификация Флинна (Flynn), но даже она является очень грубым приближением. Классификация приведена в табл. 8.2.

Таблица 8.2. Классификация компьютеров параллельного действия, разработанная Флинном

В основе классификации лежат два понятия: потоки команд и потоки данных. Поток команд соответствует счетчику команд. Система с п процессорами имеет п счетчиков команд и, следовательно, п потоков команд.

Поток данных состоит из набора операндов. В примере с вычислением температуры, приведенном выше, было несколько потоков данных, один для каждого датчика.

Потоки команд и данных в какой-то степени независимы, поэтому существует 4 комбинации (см. табл. 8.2). SISD (Single Instruction stream Single Data stream —

один поток команд, один поток данных) — это классический последовательный компьютер фон Неймана. Он содержит один поток команд и один поток данных и может выполнять только одно действие одномоментно. Машины SIMD (Single Instruction stream Multiple Data stream — один поток команд, несколько потоков данных) содержат один блок управления, выдающий по одной команде, но при этом есть несколько АЛУ, которые могут обрабатывать несколько наборов данных одновременно. ILLIAC IV (см. рис. 2.6) — прототип машин SIMD. Существуют и современные машины SIMD. Они применяются для научных вычислений.

Машины MISD (Multiple Instruction stream Single Data stream — несколько потоков команд, один потокданных) — несколькостранная категория. Здесьнесколько команд оперируют одним набором данных. Трудно сказать, существуют ли такие машины. Однако некоторые считают машинами MISD машины с конвейерами.

Последняя категория — машины MIMD (Multiple Instruction stream Multiple Data stream — несколько потоков команд, несколько потоков данных). Здесь несколько независимых процессоров работают как часть большой системы. В эту категорию попадает большинство параллельных процессоров. И мультипроцессоры, и мультикомпьютеры — это машины MIMD.

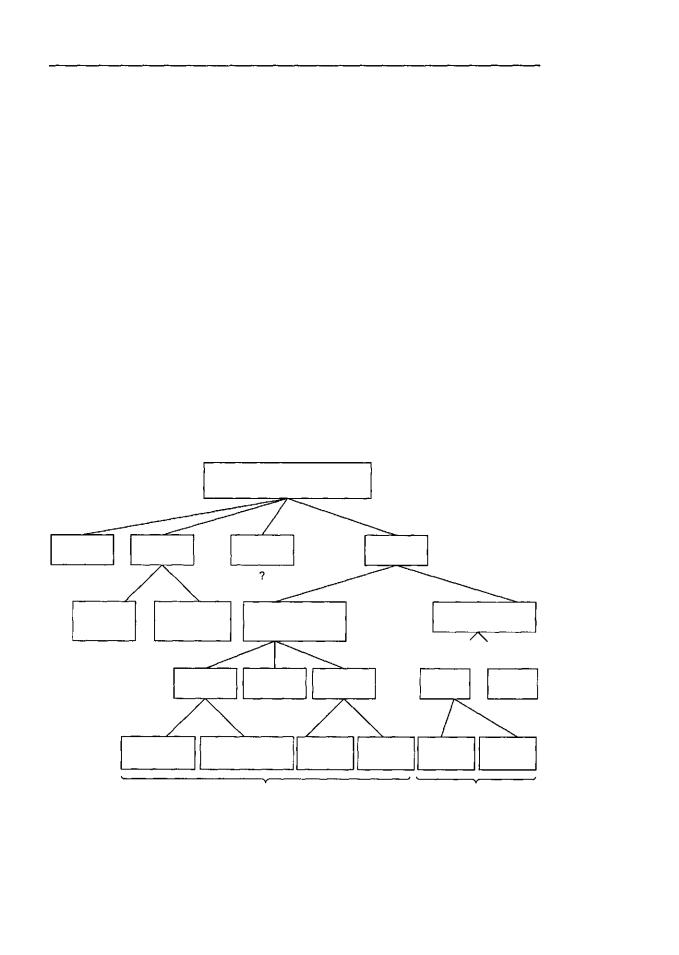
Мы расширили классификацию Флинна (схема на рис. 8.12). Машины SIMD распались на две подгруппы. В первую подгруппу попадают многочисленные суперкомпьютеры и другие машины, которые оперируют векторами, выполняя одну и ту же операцию над каждым элементом вектора. Во вторую подгруппу попадают машины типа ILLIAC IV, в которых главный блок управления посылает команды нескольким независимым АЛУ.

Архитектуры компьютеров параллельного действия

(Фон Нейман)

5 86 Глава 8. Архитектуры компьютеров параллельного действия

В нашей классификации категория MIMD распалась на мультипроцессоры (машины с памятью совместного использования) и мультикомпьютеры (машины с передачей сообщений). Существует три типа мультипроцессоров. Они отличаются друг от друга по способу реализации памяти совместного использования. Они называются UMA (Uniform Memory Access — архитектура с однородным досту-

пом к памяти), NUMA (NonUniform Memory Access — архитектура с неоднородным доступом к памяти) и СОМА (Cache Only Memory Access — архитектура сдоступомтолько ккэш-памяти). В машинах UMАкаждый процессоримеет одно и то же время доступа к любому модулю памяти. Иными словами, каждое слово памяти можно считать с той же скоростью, что и любое другое слово памяти. Если это технически невозможно, самые быстрые обращения замедляются, чтобы соответствовать самым медленным, поэтому программисты не увидят никакой разницы. Это и значит «однородный». Такая однородность делает производительностьпредсказуемой, аэтот фактороченьважендля написания эффективной программы.

Мультипроцессор NUMA, напротив, не обладает этим свойством. Обычно есть такой модуль памяти, который расположен близко к каждому процессору, и доступ к этому модулю памяти происходит гораздо быстрее, чем к другим. С точки зрения производительности очень важно, куда помещаются программа и данные. Машины СОМА тоже с неоднородным доступом, но по другой причине. Подробнее каждый из этих трех типов мы рассмотрим позднее, когда будем изучать соответствующие подкатегории.

Во вторую подкатегорию машин MIMD попадают мультикомпьютеры, которые в отличие от мультипроцессоров не имеют памяти совместного использования на архитектурном уровне. Другими словами, операционная система в процессоре мультикомпьютера не может получить доступ к памяти, относящейся к другому процессору, просто путем выполнения команды LOAD. Ему приходится отправлять сообщение и ждать ответа. Именно способность операционной системы считывать слово из отдаленного модуля памяти с помощью команды LOAD отличает мультипроцессоры от мультикомпьютеров. Как мы уже говорили, даже в мультикомпьютере пользовательские программы могут обращаться к другим модулям памяти с помощью команд LOAD и STORE, но эту иллюзию создает операционная система, ане аппаратное обеспечение. Разница незначительна, но очень важна. Так какмультикомпьютеры не имеют прямогодоступа к отдаленным модулям памяти, они иногда называются машинами NORMA (NO Remote Memory Access — без доступа к от-

даленным модулям памяти).

Мультикомпьютеры можно разделить на две категории. Первая категория содержит процессоры МРР (Massively Parallel Processors — процессоры с массовым параллелизмом) — дорогостоящие суперкомпьютеры, которые состоят из большого количества процессоров, связанных высокоскоростной коммуникационной сетью. В качестве примеров можно назвать Cray T3E и IBM SP/2.

Вторая категория мультикомпьютеров включает рабочие станции, которые связываются с помощью уже имеющейся технологии соединения. Эти примитивные машины называются NOW (Network of Workstations — сеть рабочих станций) и COW (Cluster of Workstattions — кластер рабочих станций).

В следующих разделах мы подробно рассмотрим машины SIMD, мультипроцессоры MIMD и мультикомпьютеры MIMD. Цель — показать, что собой представляет каждый из этих типов, что собой представляют подкатегории и каковы ключевые принципы разработки. В качестве иллюстраций мы рассмотрим несколько конкретных примеров.

Компьютеры SIMD

Компьютеры SIMD (Single Instruction Stream Multiple Data Stream — один поток команд, несколько потоков данных) используются для решения научных и технических задач с векторами и массивами. Такая машина содержит один блок управления, который выполняет команды по одной, но каждая команда оперирует несколькими элементами данных. Два основных типа компьютеров SIMD — это массивно-параллельные процессоры (array processors) и векторные процессоры (vector processors). Рассмотрим каждый из этих типов по отдельности.

Массивно-параллельные процессоры

Идея массивно-параллельных процессоров была впервые предложена более 40 лет назад [151]. Однакопрошлоещеоколо 10лет,преждечемтакойпроцессор (ILLIАС IV) был построен для NASA. С тех пор другие компании создали несколько коммерческих массивно-параллельных процессоров, в том числе СМ-2 и Maspar MP-2, но ни один из них не пользовался популярностью на компьютерном рынке.

В массивно-параллельном процессоре содержится один блок управления, который передает сигналы, чтобы запустить несколько обрабатывающих элементов, как показано на рис. 2.6. Каждый обрабатывающий элемент состоит из процессора или усовершенствованного АЛУ и, как правило, локальной памяти.

Хотя все массивно-параллельные процессоры соответствуют этой общей модели, они могут отличаться друг от друга в некоторых моментах. Первый вопрос — это структура обрабатывающего элемента. Она может быть различной — от чрезвычайно простой до чрезвычайно сложной. Самые простые обрабатывающие элементы — 1-битные АЛУ (как в СМ-2). В такой машине каждый АЛУ получает два 1-битных операнда из своей локальной памяти плюс бит из слова состояния программы (например, бит переноса). Результат операции — 1 бит данных и несколько флаговых битов. Чтобы совершить сложение двух целых 32-битных чисел, блоку управления нужно транслировать команду 1-битного сложения 32 раза. Если на одну команду затрачивается 600 не, то для сложения целых чисел потребуется 19,2 мке, то есть получается медленнее, чем в первоначальной IBM PC. Но при наличии 65 536 обрабатывающих элементов можно получить более трех миллиардов сложений в секунду при времени сложения 300 пикосекунд.

Обрабатывающим элементом может быть 8-битное АЛУ, 32-битное АЛУ или более мощное устройство, способное выполнять операции с плавающей точкой. В какой-то степени выбор типа обрабатывающего элемента зависит от типа целей машины. Операции с плавающей точкой могут потребоваться для сложных мате-

5 8 8 Глава 8. Архитектуры компьютеров параллельного действия

матических расчетов (хотя при этом существенно сократится число обрабатывающих элементов), но для информационного поиска они не нужны.

Второй вопрос — как связываются обрабатывающие элементы друг с другом. Здесь применимы практически все топологии, приведенные на рис. 8.4. Чаще всего используются прямоугольные решетки, поскольку они подходят для задач с матрицами и отображениями и хорошо применимы к большим размерам, так как с добавлением новых процессоров автоматически увеличивается пропускная способность.

Третий вопрос — какую локальную автономию имеют обрабатывающие элементы. Блок управления сообщает, какую команду нужно выполнить, но во многих массивно-параллельных процессорах каждый обрабатывающий элемент может выбирать на основе некоторых локальныхданных (например, на основе битов кода условия), выполнять ему эту команду или нет. Эта особенность придает процессору значительную гибкость.

Векторные процессоры

Второй тип машины SIMD — векторный процессор. Он более популярен на рынке. Машины, разработанные Сеймуром Креем (Seymour Cray) для Cray Research (сейчас это часть Silicon Graphics), — Сгау-1 в 1976 году, а затем С90 и Т90 доминировали в научной сфере на протяжении десятилетий. В этом разделе мы рассмотрим основные принципы, которые используются при создании таких высокопроизводительных компьютеров.

Типичное приложение для быстрой переработки больших объемов цифровых данных полно таких выражений, как:

for(i=0: i<n: i++) a[i]-b[i]+c[i];

где a, b и с — это векторы1 (массивы чисел), обычно с плавающей точкой. Цикл приказывает компьютеру сложить i-e элементы векторов b и с, и сохранить результат в i-м элементе массива а. Программа определяет, что элементы должны складываться последовательно, но обычно порядок не играет никакой роли.

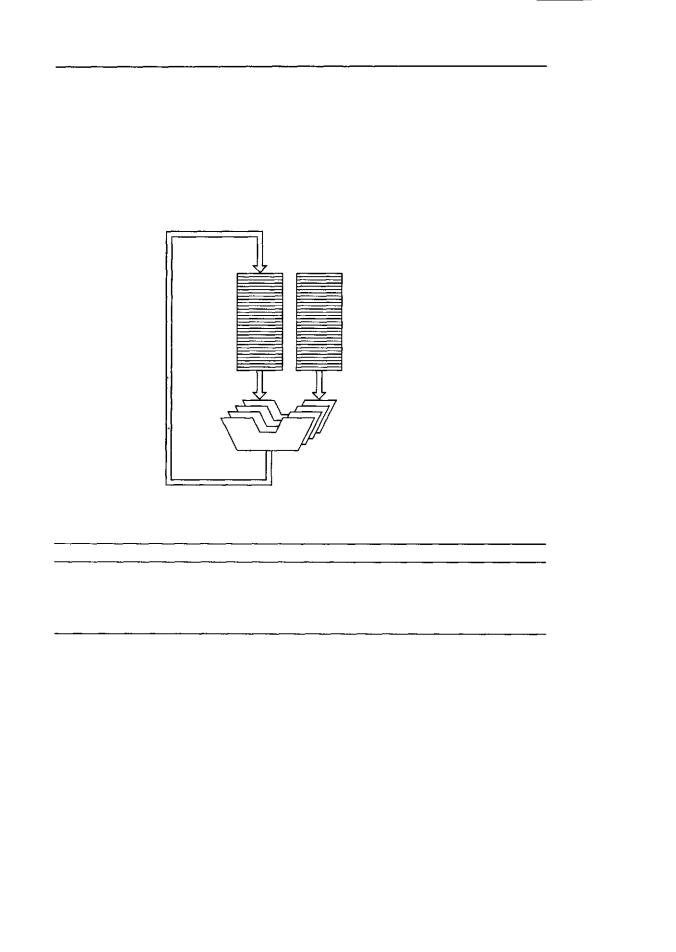
На рис. 8.13 изображено векторное АЛУ. Такая машина на входе получает два n-элементных вектора и обрабатывает соответствующие элементы параллельно, используя векторное АЛУ, которое может оперировать п элементами одновременно. В результате получается вектор. Входные и выходные векторы могут сохраняться в памяти или в специальных векторных регистрах.

Векторные компьютеры применяются и для скалярных (невекторных) операций, а также для смешанных векторно-скалярных операций. Основные типы векторных операций приведены в табл. 8.3. Первая из них, U, выполняет ту или иную операцию (например, квадратный корень или косинус) над каждым элементом одного вектора. Вторая, f2, на входе получает вектор, а на выходе выдает скалярное значение. Типичный пример — суммирование всех элементов. Третья, f3, выполняет бинарную операцию над двумя векторами, например сложение соответствую-

1Строго говоря, использование термина «вектор» в данном контексте неправомочно, хотя уже много лет говорят именно «вектор». Дело в том, что вектор, в отличие от одномерной матрицы, имеет метрику, тогда как одномерный массив представляет собой просто определенным образом упорядоченный набор значений, характеризующих некоторый объект. — Примеч. научн. ред.

щихэлементов. Наконец, четвертая, U, соединяетскалярный операндс векторным. Типичный пример — умножение каждого элемента вектора на константу. Иногда быстрее переделать скалярный операнд в вектор, каждое значение которого равно скалярному операнду, а затем выполнить операцию над двумя векторами.

Все обычные операции с векторами могут производиться с использованием этих четырех форм. Например, чтобы получить скалярное произведение двух векторов, нужно сначала перемножить соответствующие элементы векторов (f3), а затем сложить полученные результаты (f2).

Входныевекторы

ВекторноеАЛУ

Рис. 8.13. ВекторноеАЛУ

Таблица 8.3. Комбинации векторных и скалярных операций

На практике суперкомпьютеры редко строятся по схеме, изображенной на рис. 8.13. Причина не техническая — такую машину вполне можно построить, а экономическая. Создание компьютера с 64 высокоскоростными АЛУ слишком дорого обойдется.

Обычно векторные процессоры сочетаются с конвейерами. Операции с плавающей точкой достаточно сложны. Они требуют выполнения нескольких шагов, а для выполнения любой многошаговой операции лучше использовать конвейер. Если вы не знакомы с арифметикой с плавающей точкой, обратитесь к приложению Б.

Рассмотрим табл. 8.4. В данном примере нормализованное число имеет мантиссу больше 1, но меньше 10 или равную 1. Здесь требуется вычесть 9,212x10" из 1,082хЮ12.

5 9 0 Глава 8. Архитектуры компьютеров параллельного действия

Таблица 8.4. Вычитание чисел с плавающей точкой

Чтобы из одного числа с плавающей точкой вычесть другое число с плавающей точкой, сначала нужно подогнать их таким образом, чтобы их экспоненты имели одно и то же значение. В нашем примере мы можем либо преобразовать уменьшаемое (число, из которого производится вычитание) в 10,82x10", либо преобразовать вычитаемое (число, которое вычитается) в 0,9212х1012. При любом преобразовании мы рискуем. Увеличение экспоненты может привести к антипереполнению (исчезновению значащих разрядов) мантиссы, а уменьшение экспоненты может вызватьпереполнениемантиссы. Антипереполнениеменееопасно, посколькучисло с антипереполнением можно округлить нулем. Поэтому мы выбираем первый путь. Приведя обе экспоненты к 12, мы получаем значения, которые показаны в табл. 8.4 на шаге 2. Затем мы выполняем вычитание, а потом нормализуем результат.

Конвейеризацию можно применять к циклу for, приведенному в начале раздела.

Втабл. 8.5 показана работа конвейеризированного сумматора с плавающей точкой.

Вкаждом цикле на первой стадии вызывается пара операндов. На второй стадии меньшая экспонента подгоняется таким образом, чтобы соответствовать большей. На третьей стадии выполняется операция, а на четвертой стадии нормализуется результат. Таким образом, в каждом цикле из конвейера выходит один результат.

Таблица8.5. Работа конвейеризированногосумматорас плавающейточкой

Существенное различие между использованием конвейера для операций над векторами и использованием его для выполнения обычных команд — отсутствие скачков при работе с векторами. Каждый цикл используется полностью, и никаких пустых циклов нет.

Векторный суперкомпьютер Сгау-1

Суперкомпьютеры обычно содержат несколько АЛУ, каждое из которых предназначено для выполнения определенной операции, и все они могут работать параллельно. В качестве примера рассмотрим суперкомпьютер Сгау-1. Он больше не используется, но зато имеет простую архитектуру типа RISC, поэтому его очень удобно применять в учебных целях, и к тому же его архитектуру можно встретить во многих современных векторных суперкомпьютерах.

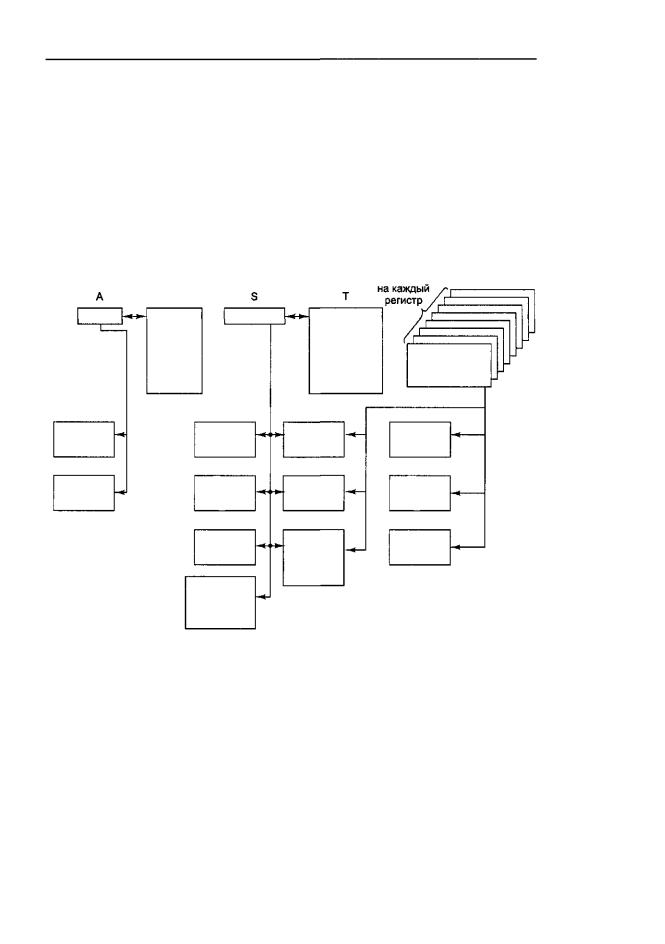
Машина Сгау-1 регистровая (что типично для машин типа RISC), большинство команд 16-битные, состоят из 7-битного кода операции и трех 3-битных номеров регистров для трех операндов. Имеется пять типов регистров (рис. 8.14). Восемь 24-битных регистров А используются для обращения к памяти. 64 24-бит- ных регистра В используются для хранения регистров А, когда они не нужны, чтобы не записывать их обратно в память. Восемь 64-битных регистров S предназначены для хранения скалярных величин (целых чисел и чисел с плавающей точкой). Значения этих регистров можно использовать в качестве операндов как для операций с целыми числами, так и для операций над числами с плавающей точкой. 64 64-битных регистра Т — это регистры для хранения регистров S, опятьтаки для сокращения количество операций LOAD и STORE.

Блокивычисления точкой генеральной совокупности

Рис.8.14.РегистрыифункциональныеблокимашиныСгау-1

Самый интересный набор регистров — это группа из восьми векторных регистров. Каждый такой регистр может содержать 64-элементный вектор с плавающей точкой. В одной 16-битной команде можно сложить, вычесть или умножить два вектора. Операция деления невозможна, но можно вычислить обратную величину. Векторные регистры могут загружаться из памяти, сохраняться в память, но такие перемещения выполнять очень невыгодно, поэтому их следует свести к минимуму. Во всех векторных операциях используются регистровые операнды.

5 9 2 Глава 8. Архитектуры компьютеров параллельного действия

Не всегда в суперкомпьютерах операнды должны находиться в регистрах. Например, машина CDC Cyber 205 выполняла операции над векторами в памяти. Такой подход позволял работать с векторами произвольной длины, но это сильно снижало скорость работы машины.

Сгау-1 содержит 12 различных функциональных блоков (см. рис. 8.14). Два из них предназначены для арифметических действий с 24-битными адресами. Четыре нужны для операций с 64-битными целыми числами. Сгау-1 не имеет блока для целочисленного умножения (хотя есть блок для перемножения чисел с плавающей точкой). Оставшиеся шесть блоков работают над векторами. Все они конвейеризированы. Блоки сложения, умножения и вычисления обратной величины работают как над скалярными числами с плавающей точкой, так и над векторами.

Как и многие другие векторные компьютеры, Cray-1 допускает операции сцепления. Например, чтобы вычислить выражение

R1=R1*R2+R3

где Rl, R2 и R3 — векторные регистры, машина выполнит векторное умножение элемент за элементом, сохранит результат где-нибудь, а затем выполнит векторное сложение. При сцеплении, как только первые элементы перемножены, произведение сразу направляется в сумматор вместе с первым элементом регистра R3. Сохранения промежуточного результата не требуется. Такая технология значительно улучшает производительность.

Интересно рассмотреть абсолютную производительность Сгау-1. Тактовый генератор работает с частотой 80 МГц, а объем основной памяти составляет 8 Мбайт. В то время (в середине — конце 70-х) это был самый мощный компьютер в мире. Сегодня вряд ли кто-нибудь сможет купить компьютер с таким медленным тактовым генератором и такой маленькой памятью — их уже никто не производит. Это наблюдение показывает, как быстро развивается компьютерная промышленность.

Мультипроцессоры с памятью совместного использования

Как показано на рис. 8.12, системы MIMD можно разделить на мультипроцессоры и мультикомпьютеры. В этом разделе мы рассмотрим мультипроцессоры, а в следующем — мультикомпьютеры. Мультипроцессор — это компьютерная система, которая содержит несколько процессоров и одно адресное пространство, видимое для всех процессоров. Он запускает одну копию операционной системы с одним набором таблиц, в том числе таблицами, которые следят, какие страницы памяти заняты, а какие свободны. Когда процесс блокируется, его процессор сохраняет свое состояние в таблицах операционной системы, а затем просматривает эти таблицы для нахождения другого процесса, который нужно запустить. Именно наличие одного отображения и отличает мультипроцессор от мультикомпьютера.

Мультипроцессор, как и все компьютеры, должен содержать устройства вводавывода (диски, сетевые адаптеры и т. п.). В одних мультипроцессорных системах только определенные процессоры имеют доступ к устройствам ввода-вывода и, следовательно, имеют специальную функцию ввода-вывода. В других мультипро-