Лабораторна робота № 5-7

Визначення дифракції Фраунгофера

на дифракційній гратці

Мета роботи: ознайомлення з прозорою дифракційною траткою, визна­чення довжини хвилі джерела світла, а також роздільної здатності дифракційної гратки та інтенсивності дифракцій­них максимумів.

Прилади і матеріали: джерело світла - гелій-неоновий лазер, дифракцій­на гратка, екран з шкалою (ціна поділки 1 мм), лю­ксметр Ю116, оптична лава.

Теоретичні відомості

Плоска прозора дифракційна гратка це - прозора пластинка з великою кількістю N (до 2400 на довжині 1 мм) тонких паралельних щілин однако­вої ширини та однакової віддалі між їх серединами (або іншими відпові­дними точками). Щілини гратки утворюють упорядковану структуру. Ця структура має різний коефіцієнт пропускання світла через щілини та про­міжки між ними, тому гратку такого типу називають амплітудною.

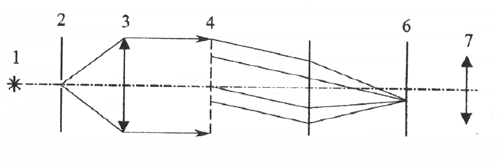
Рис.1

Віддаль називається періодом (або сталою) дифракційної гратки. На рис. 1 зображено хід променів через дифракційну гратку згідно з схемою дифракції Фраунгофера. Монохроматичне світло від джерела 1 попа­дає на щілину 2, що знаходиться в фокальній площині об'єктиву паралель­ний пучок променів. Результуючий пучок дійде до дифракційної гратки 4 практично паралельним, тобто плоским пучком променів. Ці промені ди-фрагують при проходженні через гратку і створюють вторинні конкретні розбіжні пучки під кутами дифракції Пучки, пройшовши через об'єктив 5 зорової труби, дають в його фокальній площині 6 дифра­кційну картину, яка є зображенням щілини 2 як результату інтерференції когерентних коливань, що дійшли до площини 6. Це зображення можна спостерігати з допомогою об'єктива 7. При відсутності гратки в фокальній площині 6 спостерігатиметься звичайне зображення щілини 2.

У відповідності з принципом Гюйгенса-Френеля розподіл інтенсивності в дифракційній картині визначається суперпозицією хвиль, що прийшли в точку спостереження від різних щілин дифракційної гратки. При цьому ам­плітуди всіх інтерферуючих хвиль для певного кута практично однакові, а фази складають арифметичну прогресію. Нехай падаюча на гратку світ­лова хвиля розповсюджується перпендикулярно до її поверхні. Інтенсив­ність дифрагованого світла буде максимальна для тих кутів, для яких хвилі, що приходять в точку спостереження від всіх щілин гратки, мають однакові фази. Для таких напрямків справедливе співвідношення:

(т - ціле число). (1)

Точна теорія гратки враховує як інтерференцію хвиль, що приходять від різних щілин, так і дифракцію на кожній щілині. Розрахунки показують. Що інтенсивність J світла, яке поширюється під кутом до нормалі, дорі­внює

, (2)

де - хвильове число, - інтенсивність, створювана однією щілиною а напрямку .

Аналіз виразу (2) показує, що при великій кількості щілин N світло, пройшовши крізь гратку, поширюється тільки вздовж певних різко обме­жених напрямків, які визначаються співвідношенням (1). Залежність інтен­сивності світла від кута спостереження зображена на рис. 2.

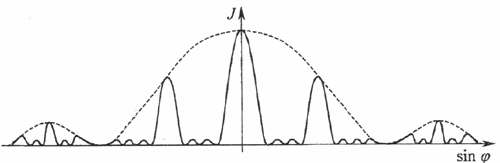
Рис.2

Пунктирна крива зображає інтенсивність від однієї щілини, помножену

на N . Суцільна крива відповідає основним максимумам, а також додатко­вим максимумам та мінімумам.

Як випливає з (1) кути, при яких спостерігаються світлові максимуми, залежать від довжини хвилі . Прит = 0 максимуми інтенсивності для всіх довжин хвиль розташовуються при = 0 і накладаються один на од­ного. Це - максимум нульового порядку. Максимуми першого, другого і т.д. порядків розміщуються симетрично відносно нульового.

У залежності від віддалі джерела світла та точки спостереження від пе­решкоди (гратки) розрізняють дифракцію Френеля і дифракцію Фраунго-фера. Якщо ці віддалі досить великі, то промені, падаючі на перешкоду, а також ті, які приходять в точку спостереження, можна вважати паралель­ними, та має місце дифракція Фраунгофера.

У даній лабораторній роботі джерелом світла являється гелій-неоновий лазер. Його випромінювання характеризується високим ступенем монохро-матичності - когерентності в часі, просторової когерентності, значною по­тужністю та малою кутовою розбіжністю.

Для виконання роботи використовується оптична лава 1, розміщення приладів на якій зображено на рис.З, 2 - оптичний квантовий генератор (лазер) з джерелом живлення; 3 - дифракційна гратка; 4 - екран.

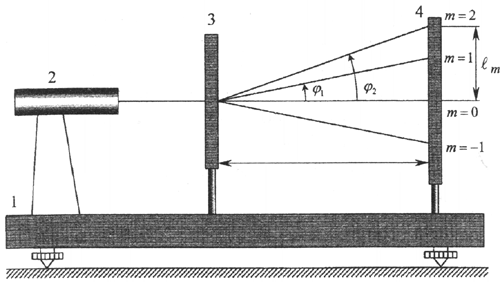
Рис.3

З формули (1) можна визначити довжину хвилі , якщо відомі кут, порядок максимуму т та стала дифракційної гратки :

. (3)

Але при малих кутах , a можна знайти за співвідношенням:

, (4)

таким чином:

, (5)

де L - віддаль від гратки до екрану;

- віддаль від центру дифракційної картини до от- того максимуму;

d - стала дифракційної гратки.

Розподіл інтенсивності в дифракційній картині досліджується з допомо­гою люксметра Ю 116.

Звертаємо увагу на те, що попадання в очі прямого лазерного пучка небезпечне для зору! При роботі з лазером його світло можна спостеріга­ти тільки після відбивання від розсіюючих поверхонь.