5

Лабораторная работа № 31

определение напряжённости магнитного поля в центре кругового тока

Цель работы

1. Проверить закон Био-Савара-Лапласа.

2. Определить напряжённость магнитного поля в лаборатории.

Теоретическое введение

Если по проводнику протекает электрический ток, то в окружающем его пространстве возникает магнитное поле. Количественными характеристиками магнитного поля являются магнитная индукция (Тл) и напряжённость (А/м). Эти величины связаны между собой соотношением:

, (1)

где μ_о = 4π∙10^-7 Гн/м - магнитная постоянная, μ – магнитная проницаемость среды.

Численное значение напряжённости dH магнитного поля, создаваемого элементом проводника dl, по которому идёт ток силой I, в точке, отстоящей от данного элемента проводника на расстояние r, определяется по закону Био-Савара-Лапласа:

(2)

где α – угол между направлением тока в данном элементе проводника dl и радиус-вектором , проведённым из этого элемента в точку, в которой определяется напряжённость поля.

Направление вектора находится по правилу буравчика.

Вектор напряжённости общего магнитного поля, создаваемого всем проводником, есть векторная сумма напряжённостей полей, создаваемых отдельными элементами:

, (3)

где интегрирование ведётся по всей длине проводника.

Таким способом можно рассчитать и напряжённость магнитного поля в центре кругового витка с током. В этом случае для всех элементов проводника расстояние r до точки, в которой определяется напряжённость (центра), равно радиусу витка R, а угол α = 90^о. В центре кругового тока все векторы напряжённостей, создаваемых отдельными элементами, совпадают по направлению (перпендикулярны плоскости витка), поэтому

. (4)

В последней формуле интегрирование ведётся по всей длине кругового витка. Из (4) и (2), с учётом того, что r = R и sin α = sin 90^о = 1, получаем:

. (5)

Напряжённость в центре плоской короткой катушки, содержащей N одинаковых витков,

. (6)

В данной работе проводится экспериментальная проверка последней формулы и, следовательно, проверка справедливости закона Био-Савара-Лапласа (2).

Описание установки и метода

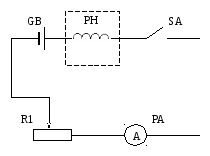
Установка, схема которой приведена на рис. 1, состоит из следующих последовательно соединённых элементов:

• источника постоянного тока GB,

• выключателя SA,

• реостата для изменения силы тока в цепи R1,

• амперметра РА,

- тангенс-гальванометра РН – прибора, предназначенного для измерения напряжённости магнитного поля в центре кругового тока.

Рисунок 1. Принципиальная схема установки

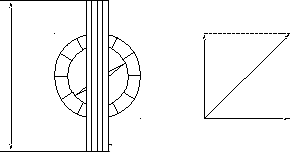
На рис. 2 показан вид сверху на тангенс-гальванометр. Он представляет собой плоскую короткую вертикальную катушку радиусом R с числом витков N, в центре которой на вертикальном острие расположена короткая магнитная стрелка NS, способная вращаться в горизонтальной плоскости.

N

2R S

φ

S

Рисунок 2. Вид сверху на тангенс-гальванометр

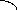
Принцип измерения основан на том, что, если при отсутствии тока в катушке стрелка ориентирована вдоль силовых линий магнитного поля, имеющегося в лаборатории, то при пропускании тока появляется собственное магнитное поле катушки, заставляющее стрелку отклониться на некоторый угол φ.

В исходном состоянии, когда тока в цепи нет, катушку надо расположить так, чтобы горизонтальная составляющая вектора напряжённости магнитного поля лаборатории лежала в её плоскости. Для этого катушку без тока поворачивают так, чтобы стрелка одним из концов была направлена на нулевое деление круговой шкалы, жёстко связанной с катушкой. При пропускании тока возникает собственное магнитное поле катушки, вектор напряжённости которогоперпендикулярен плоскости витков и, тем самым, вектору . Стрелка повернётся на угол φ и установится вдоль вектора напряжённости результирующего поля . Из рис. 2 видно, что

. (7)

Из формул (6) и (7) вытекает, что, если закон Био-Савара-Лапласа справедлив, то тангенс угла отклонения стрелки прямо пропорционален силе тока:

. (8)

Отсюда же следует формула для определения напряжённости магнитного поля лаборатории:

. (9)

Порядок выполнения работы

1. Собрать схему, показанную на рис. 1.

2. Не подавая ток в цепь (I=0), вращением катушки вокруг вертикальной оси совместить её плоскость со стрелкой тангенс-гальванометра.

3. Изменяя силу тока в контуре от 0 до 1А, снять зависимость φ(I) (8-10 точек). Результаты занести в таблицу 1.

4. Определить и записать число витков в контуре N, радиус витков R и погрешность ∆R.

Таблица 1 Таблица расчетных и экспериментальных данных

№ п/п	I, А	φ	tgφ

Обработка результатов измерений

1. Построить график зависимости tg φ(I). Сделать вывод о справедливости закона Био-Савара-Лапласа.

2. Определить, в каком из опытов угол φ был наиболее близок к 45^о (в этом случае погрешность расчёта Н_Л минимальна). Для этого опыта рассчитать по формуле (9) горизонтальную составляющую Н_Л магнитного поля лаборатории. Погрешность ∆Н_Л рассчитать по формуле:

∆Н_Л = Н_Л∙∙ , (10)

где ∆φ = 0,5^о (перевести в радианы), ∆I определить по классу точности прибора РА.

Сравнить найденное значение Н_Л с известным значением напряжённости магнитного поля Земли для Брянска Н_ЗМ = (16,0 ± 0,5) А/м. Сделать вывод о влиянии лабораторного оборудования на магнитное поле Земли.

Контрольные вопросы

1. Характеристики магнитного поля: напряжённость и индукция. Их взаимосвязь и единицы измерения.

2. Закон Био-Савара-Лапласа. Правило буравчика.

3. Вывод формулы для напряжённости магнитного поля в центре кругового тока.

4. Вывод формулы для напряжённости магнитного поля прямолинейного проводника с током.

5. Принцип действия тангенс-гальванометра.

Список рекомендованной литературы

1. Трофимова Т.И. Курс физики: Учебное пособие для вузов. – 7-е изд., испр. – М.: Высшая школа, 2003. – § 109, 110, 112.

2. Детлаф А.А., Яворский Б.М. Курс физики: Учебное пособие для вузов. – 2-е изд., испр. и доп. - М.: Высшая школа, 1999. – §§ 21.1, 22.1, 22.2.

3. Савельев И.В. Курс общей физики: Учеб: В 3-х т. Т.2: Электричество и магнетизм. Волны. Оптика. – 3-е изд., испр. - М.: Наука., 1989. – § 40, 42.

4. Грабовский Р.И. Курс физики (для сельскохозяйственных вузов): Учеб. пособие. – 5-е изд., перераб. и доп. – М.: Высшая школа, 1980. – Ч.2 §§ 24, 26, 27.