
55 Лабораторная работа № 39
ИССЛЕДОВАНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ
В КОЛЕБАТЕЛЬНОМ RLC-КОНТУРЕ
Цель работы
-
Проверить формулу Томсона для расчёта периода колебаний Т в колебателъном LC-контуре.
-
Определить коэффициент затухания δ при различных значениях сопротивления R контура.
-
Проверить применимость формулы Томсона к контуру с потерями.
Краткие теоретические сведения
Колебательный контур – это цепь, состоящая из катушки индуктивности L, конденсатора С и резистора R. Если конденсатор зарядить, то в контуре возникают электромагнитные колебания, при которых электрические величины (заряды, напряжения и токи) периодически изменяются.
Если сопротивление контура пренебрежимо мало (R≈0), то возникающие колебания являются гармоническими (незатухающими) и сопровождаются взаимным превращением энергии электрического и магнитного полей. Такой контур называется идеальным (рис. 1а).
Всякий реальный контур (рис. 1б) обладает активным сопротивлением (R≠0), поэтому первоначально запасённая в контуре энергия, расходуется на нагревание этого сопротивления, и возникающие колебания являются затухающими.

Затухающие колебания – это колебания, амплитуда которых уменьшается с течением времени из-за потерь энергии в реальной колебательной системе.
Закон затухания колебаний определяется параметрами колебательной системы.
Амплитуда UЗ затухающих колебаний уменьшается с течением времени по экспоненте (пунктирная кривая на графиках колебаний таблицы 1).
Промежуток времени τ, в течение которого амплитуда колебаний уменьшается в е раз, называется временем релаксации.
Величина, обратная времени релаксации и определяемая параметрами колебательного контура, называется коэффициентом затухания δ:
![]()
![]() .
(1)
.
(1)
Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако, если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся величины. Период затухающих колебаний Tз зависит от параметров колебательного контура (индуктивности L, ёмкости C и коэффициента затухания δ) и определяется по формуле:
 .
(2)
.
(2)
При отсутствии потерь энергии (R=0 δ=0) формула для расчёта периода колебаний принимает вид (формула Томсона):
![]()
![]() .
(3)
.
(3)
Формула Томсона также применима и в том случае, когда циклическая частота собственных незатухающих колебаний ω0 во много раз больше коэффициента затухания δ .
Если U(t) и U(t+T) – амплитуды двух последующих колебаний, соответствующих моментам времени, отличающимся на период, то отношение
![]() (4)
(4)
называется декрементом затухания, а логарифм отношения
ln![]() =
æ
(5)
=
æ
(5)
– логарифмическим декрементом затухания.
Связь между коэффициентом затухания δ и логарифмическим декрементом затухания æ устанавливается следующим образом:
Амплитуды двух последующих колебаний можно представить в виде:
![]() ;
; ![]() (6)
(6)
Тогда отношение двух последующих амплитуд:
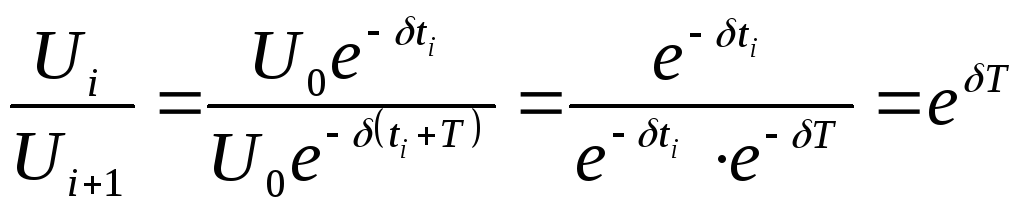 ;
(7)
;
(7)
а логарифм их отношения
ln![]() =
æ. (8)
=
æ. (8)
В таблице 1 приведены сравнительные характеристики незатухающих и затухающих колебаний применительно к колебательному контуру.
Таблица 1. Сравнительные характеристики гармонических (незатухающих) и затухающих колебаний.
|
Характеристика |
Колебания |
|
|
Незатухающие (R=0) |
Затухающие (R≠0) |
|
|
Уравнение колебаний |
UС=U0∙sin(ω0t + φ0); где U0 – амплитуда колебаний; ω0 – собственная частота колебаний; φ0 – начальная фаза колебаний (t=0) |
UС=UЗ∙sin(ωЗt + φ0); где UЗ –амплитуда колебаний; ωЗ –частота затухающих колебаний; φ0 – начальная фаза колебаний (t=0) |
|
Амплитуда U |
U0 = const |
U3 = U0∙e-δt |
|
частота ω |
|
|
|
Коэффициент затухания δ |
δ = 0 |
|
|
Период колебаний Т |
|
|
|
колебаний |
|
|
Описание установки.
Установка для исследования затухающих колебаний (см. рис. 2) содержит блок ударного возбуждения контура, собственно колебательный контур и электронный осциллограф С1-17 с калиброванной разверткой. Блок ударного возбуждения содержит понижающий трансформатор Тр, выпрямляющий диод VD1, превращающий синусоидальный сигнал в выпрямленный, стабилитрон VD2, служащий для уменьшения времени ударного возбуждения и ограничительное сопротивление Rогр, предотвращающее выход блока из строя при случайном замыкании выхода блока. Блок вырабатывает кратковременные импульсы, следующие с частотой сети (50 Гц) и напряжением порядка 10 В. В момент подачи импульса происходит зарядка конденсатора, а в промежуток времени между импульсами в контуре возникают затухающие колебания, период которых определяется по формулам (2) или (3).
Колебательный контур состоит из магазина емкостей, магазина сопротивлений и катушки индуктивности. Меняя ёмкость С магазина, изменяют период колебаний T контура, а изменяя сопротивление R магазина, изменяют вносимое в контур затухание.
Р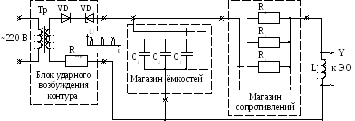 исунок
2. Схема установки для исследования
затухающих колебаний.
исунок
2. Схема установки для исследования
затухающих колебаний.
(ЭО – электронный осциллограф, Y – вход канала вертикального усиления)
Данная установка позволяет:
-
изменять сопротивление R магазина в диапазоне от 0 до 3000 Ом; при этом изменяется коэффициент затухания δ от начального δo, определяемого собственным сопротивлением RL катушки индуктивности, до максимального, при котором происходит превращение затухающих колебаний в апериодические;
-
изменять ёмкость C контура в диапазоне от 0,05 до 0,5 мкФ; при этом изменяется период Т затухающих колебаний.
Параметры затухающих колебаний определяются с помощью электронного осциллографа:
-
период колебаний Т находится с помощью калиброванной развертки осциллографа;
-
коэффициент затухания δ находится по степени относительного уменьшения амплитуд двух соседних колебаний Ui и Ui+1.
Индуктивность катушки L и ее активное сопротивление RL определяются в данной работе расчётным путём через период колебаний Т и коэффициент затухания колебаний δ.
Порядок выполнения работы
-
Собрать цепь по схеме в соответствии с рисунком 2. После проверки схемы преподавателем включить блок питания и осциллограф в сеть 220В.
-
Установить на магазине сопротивлений значение R = 0, а на магазине ёмкостей одно из значений ёмкости С в диапазоне (0,1÷0,5) мкФ (по указанию преподавателя).
-
Получить на экране осциллографа устойчивое изображение затухающих колебаний (должно наблюдаться не менее пяти периодов).
Примечание:
На передней панели осциллографа переключатель «ДЛИТЕЛЬНОСТЬ» необходимо установить в положение «200 μs/см»; переключатель «МНОЖИТЕЛЬ» – в положение «×5»; переключатель «ЗАПУСК» – в положение «+».
Ручками «УСИЛЕНИЕ» канала Y (дискретно и плавно) установить максимальную амплитуду колебаний порядка 40÷50 мм. Устойчивость изображения достигается вращением ручек «СИНХРОНИЗАЦИЯ» и «ПОДСТРОЙКА СИНХРОНИЗАЦИИ», а четкость изображения – вращением ручек «ФОКУС» и «АСТИГМАТИЗМ».
Перемещение изображения вдоль осей Х и Y производится соответственно ручками «Х↔» и «Y↨».
-
Проверка зависимости периода колебаний Т от емкости контура С.
-
Установить на магазине сопротивлений значение R = 0 Ом.
-
Установить на магазине ёмкостей начальное значение С в диапазоне 0,05÷0,25 мкФ (по указанию преподавателя).
-
Совместить максимальное значение амплитуды колебания, принятого за начальное, с левой вертикальной линией сетки шкалы (см. рис. 3). Подсчитать число периодов N, умещающихся на сетке экрана и занимаемую ими длину экрана lN в сантиметрах. Результаты измерений занести в таблицу 2.
-
Указание. При счете числа периодов по числу максимумов начальная амплитуда в расчет не принимается.
-
Изменяя значение емкости С магазина ёмкостей с шагом, заданным преподавателем, провести необходимое количество измерений по п.1.3.
Таблица 2 Зависимость периода затухающих колебаний от ёмкости контура.
|
Параметры: R = 0 Ом; «ДЛИТЕЛЬНОСТЬ» = 200 μs/см; «МНОЖИТЕЛЬ» ×5 |
||||||
|
Экспериментальные данные |
Расчетные данные |
|||||
|
№ |
С, мкФ |
N |
lN, см |
lТ, см |
Т, мс |
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
-
Исследование зависимости коэффициента затухания δ от активного сопротивления R контура.
-
Установить на магазине ёмкостей значение С в диапазоне 0,1÷0,5 мкФ (по указанию преподавателя).
-
Установить на магазине сопротивлений начальное значение R = 0 Ом.
-
Выбрать одну из горизонтальных осей сетки экрана в качестве оси Х. Установить изображение колебаний симметрично относительно выбранной оси.
-
С
 помощью ручек «УСИЛЕНИЕ» Y
(дискретно и плавно) установить
максимальную амплитуду колебания
порядка 40÷50
мм (см. рис.4).
помощью ручек «УСИЛЕНИЕ» Y
(дискретно и плавно) установить
максимальную амплитуду колебания
порядка 40÷50
мм (см. рис.4). -
Измерить (в миллиметрах) амплитуду первых четырёх колебаний, каждый раз совмещая измеряемую амплитуду с вертикальной осью, имеющей миллиметровые деления; результаты измерений занести в таблицу 4.
-
Изменяя сопротивление R магазина сопротивлений с шагом, заданным преподавателем, провести необходимое количество измерений по п.3.4. При этом максимальную амплитуду колебания необходимо поддерживать на уровне 40÷50 мм с помощью ручек «УСИЛЕНИЕ» Y (дискретно и плавно).
-
Таблица 3 Зависимость коэффициента затухания колебаний δ от сопротивления R контура.
|
Параметры: С = ___ мкФ |
||||||||||||
|
Экспериментальные данные |
Расчетные данные |
|||||||||||
|
№ |
R, Ом |
Амплитуда U, мм |
Логарифмический декремент æ |
δ,с-1 |
||||||||
|
U1 |
U2 |
U3 |
U4 |
U5 |
æ1 |
æ2 |
æ3 |
æ4 |
<æ> |
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
-
Проверка применимости формулы Томсона к контуру с потерями.
-
Установить на магазине ёмкостей значение С в диапазоне 0,1÷0,5 мкФ (по указанию преподавателя).
-
Установить на магазине сопротивлений начальное значение R = 0 Ом.
-
Произвести измерения периода затухающих колебаний Т по пункту 1.3; результаты измерений занести в таблицу 3.
-
Изменяя сопротивление R магазина сопротивлений с шагом, заданным преподавателем, провести необходимое количество измерений по п.1.3.
-
Таблица 4 Зависимость периода затухающих колебаний от сопротивления R контура.
|
Параметры: С = ___ мкФ; «ДЛИТЕЛЬНОСТЬ» = 200 μs/см; «МНОЖИТЕЛЬ» ×5 |
||||||||
|
Экспериментальные данные |
Расчетные данные |
|||||||
|
№ |
R, Ом |
N |
lN, см |
lТ, см |
Т, мс |
<Т>, мс |
∆Т, мс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|


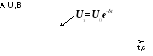
 График
График
