6. О точности вычислений

Ошибка результата определяется не только ошибкой измерений, но и ошибками вычислений. Вычисления необходимо проводить так, чтобы их ошибка была на порядок меньше ошибки результата измерений. Для этого вспомним правила математических действий с приближенными числами.

Результаты измерений – приближенные числа. В приближенном числе все цифры должны быть верными. Последней верной цифрой приближенного числа считается та цифра, ошибка в которой не превышает одной единицы ее разряда. Все цифры от 1 до 9 и нуль, если он стоит в середине или в конце числа, называются значащими. В числе 6100 – четыре значащих цифры, а в 6,1·10³ – только две, в числе 0,00209 – три, т.к. нули слева от двойки незначащие.

Запись 2,39 означает, что верны все знаки до второго после запятой, а запись 2,3900 – что верны также и третий и четвертый знаки. В числе 6,30 три значащие цифры и это значит, что при измерении мы учитывали не только единицы, но и десятые и сотые, в числе 6,3 – только две значащие цифры и это значит, что мы учитывали только целые и десятые и точность этого числа в десять раз меньше.

Правила округления чисел

При округлении оставляют лишь верные знаки, остальные отбрасывают.

Правило 1. Округление достигается простым отбрасыванием цифр, если первая из отбрасываемых цифр меньше, чем 5.

Правило 2. Если первая из отбрасываемых цифр больше, чем 5, то последняя цифра увеличивается на единицу. Последняя цифра увеличивается также и в том случае, когда первая из отбрасываемых цифр 5, а за ней есть одна или несколько цифр, отличных от нуля. Например, различные округления числа 35,856 будут 35,86; 35,9; 36.

Правило 3. Если отбрасываемая цифра равна 5, а за ней нет значащих цифр, то округление производится на ближайшее четное число, т.е. последняя сохраняемая цифра остается неизменной, если она четная и увеличивается на единицу, если она нечетная. Например, 0,435 округляем до 0,44; 0,465 округляем до 0,46.

8. Пример обработки результатов измерений

Определение плотности твердых тел. Предположим, твердое тело имеет форму цилиндра. Тогда плотность ρ может быть определена по формуле:

где D – диаметр цилиндра, h – его высота, m – масса.

Пусть в результате измерений m, D, и h получены следующие данные:

№ п/п	m, г	Δm, г	D, мм	ΔD, мм	h, мм	Δh, мм	, г/см3	Δ, г/см3
1	51,2	0,1	12,68	0,07	80,3	0,15	5,11	0,07	0,013
2			12,63		80,2
3			12,52		80,3
4			12,59		80,2
5			12,61		80,1
среднее			12,61		80,2		5,11

Будем считать, что определение массы цилиндра производилось с помощью технических весов. Допустимая ошибка таких весов равна Δm = 100 мг = 0,1 г.

Определим среднее значение D̃:

Найдем погрешности отдельных измерений и их квадраты

Определим среднюю квадратичную погрешность серии измерений:

Задаем значение надежности α = 0,95 и по таблице находим коэффициент Стьюдента t_α.n=2,8 (для n = 5). Определяем границы доверительного интервала:

Так как вычисленное значение ΔD = 0,07 мм значительно превышает абсолютную ошибку микрометра, равную 0,01 мм (измерение производится микрометром), то полученное значение может служить оценкой границы доверительного интервала:

D = D̃ ± ΔD; D = (12,61 ±0,07) мм.

Определим значение h̃:

тогда:

Следовательно:

Для α = 0,95 и n = 5 коэффициент Стьюдента t_α,n = 2,8.

Определяем границы доверительного интервала

.

Так как полученное значение Δh = 0,11 мм того же порядка, что и ошибка штангенциркуля, равная 0,1 мм (измерение h производится штангенциркулем), то границы доверительного интервала следует определить по формуле:

где

Следовательно:

Вычислим среднее значение плотности ρ:

Найдем выражение для относительной погрешности:

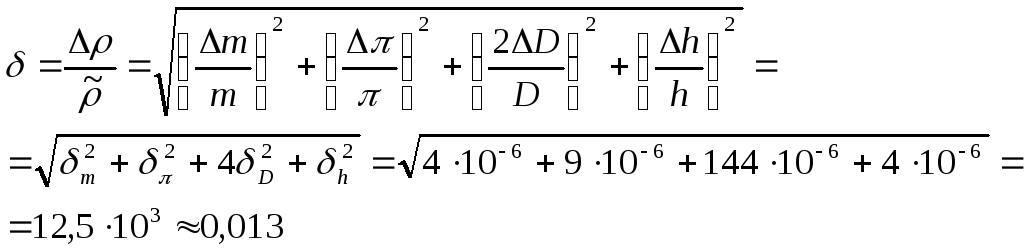
где

Окончательно имеем: