Пример выполнения варианта расчетно-графической работы.

Задание 1. Найти область решения системы неравенств. Сделать чертеж.

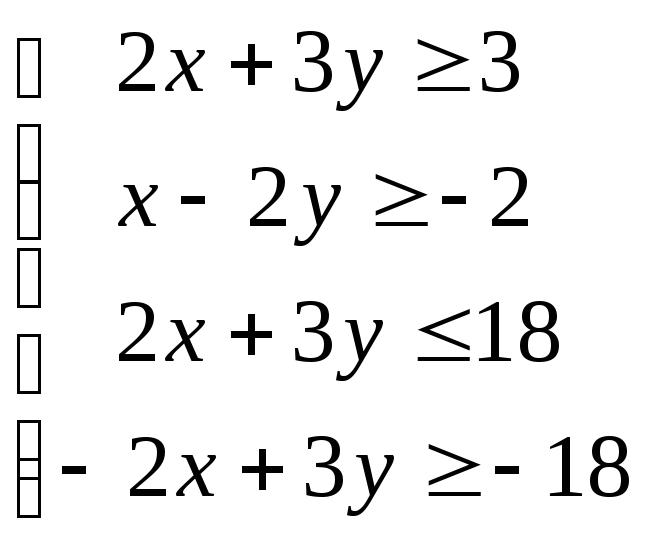
Решение.

Заменим в данной системе каждое неравенство равенством. По полученным уравнениям построим прямые. Каждая прямая разделит плоскость на две полуплоскости, в одной из которых выполняется неравенство, в другой - нет. Часть плоскости, в которой выполняются все неравенства и есть область решения.

Рис.1

Ответ. Областью решения служит четырехугольник ABCD.

Задание 2. Решить систему уравнений двумя способами:

1. Методом Гауcса

2. Матричным методом.

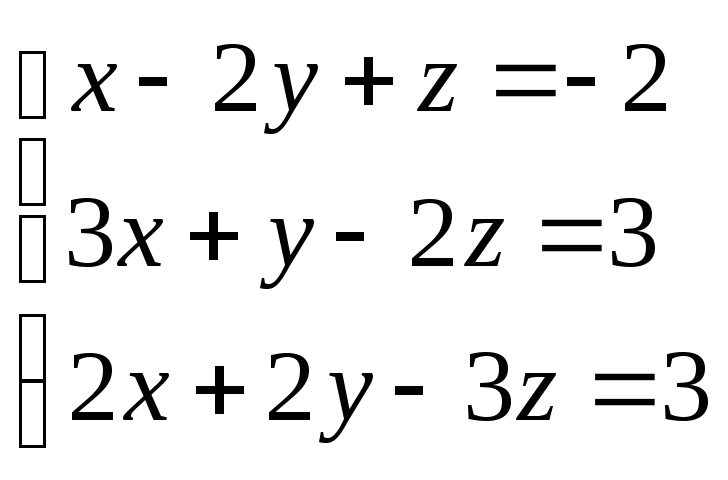
Решение.

Вычислить определитель системы ∆:

∆==

Следовательно, система имеет единственное решение.

Решим систему методом Гаусса. Составим расширенную матрицу, и, применяя элементарные преобразования, приведем ее к диагональному виду

Проверка:

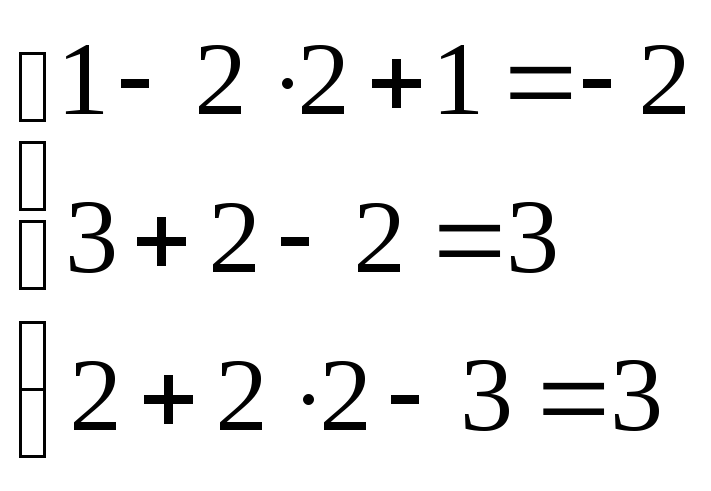
Решим систему матричным методом. Составим обратную матрицу А^-1.

Вычислим алгебраическое дополнение А_ίj:

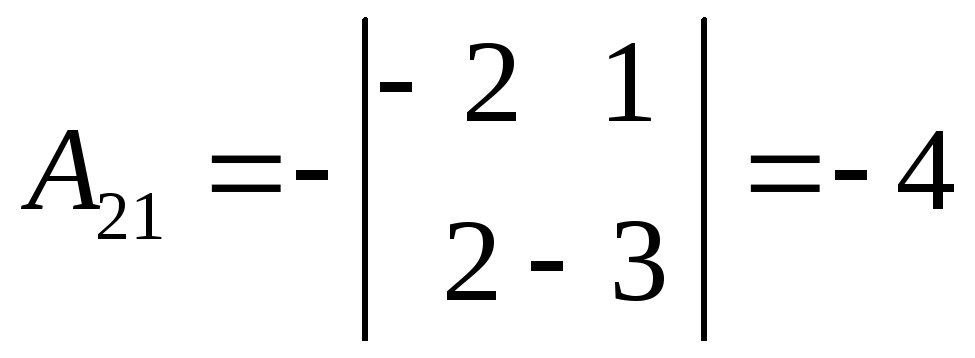
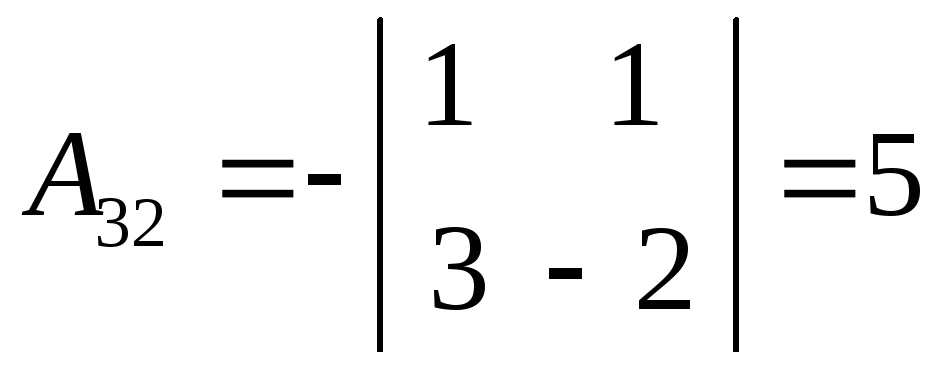
Ответ:

Задание 3. Дана пирамида:,,,.

Найти:

1)угол между ребрами и.

2)уравнение плоскости ;

3)уравнение и длину высоты, опущенной из вершины на грань;

4)угол между ребром и гранью;

5)объем пирамиды;

6)площадь грани . Сделать чертеж.

Решение.

1)Найти координаты векторов и:

= ===

Вычислим косинус угла образованного векторамии:

2)Запишем уравнение плоскости, проходящей через три точки:

Уравнение плоскости :

3)Вычислим векторное произведение векторов и:

Так как вектор векторного произведения перпендикулярен плоскости , то его можно принять за направляющий вектор высоты. Уравнения высоты будет иметь вид:

Найдем координаты точки , пересечения прямойс плоскостью. Запишем уравнение плоскости:

Уравнение высоты запишем в параметрической форме и решим систему:

; ;

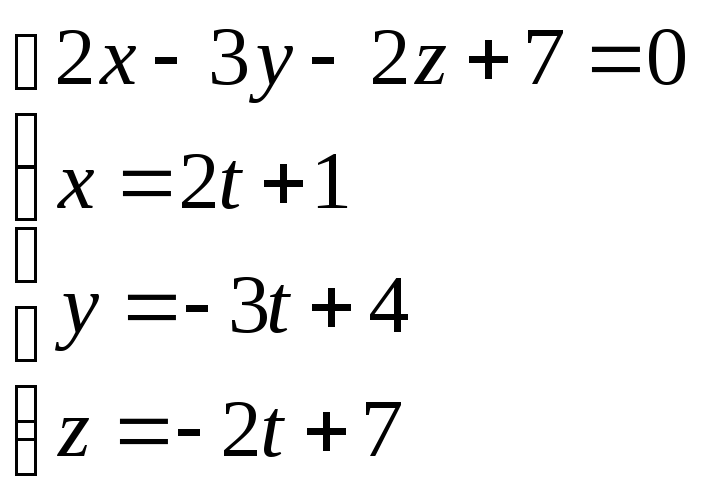
Вычислим длину высоты :

Уравнение высоты :

Длинна

4)Вычислим синус угла между ребром и гранью:

рад.

5)вычислим объем пирамиды :

ед.

6) Вычислим площадь грани :

ед

Сделаем чертеж:

Рис. 2

Задание 4. Даны векторыв некотором базисе.

Показать, что векторы образуют базис и найти координаты векторав базисе .

=,=,=,=

Решение.

Три вектора образуют базис в пространстве, если они некомпланарны. Условием компланарности трех векторов служит равенство

Вычислим смешенное произведение:

Следовательно, векторы образуют базис.

Найдем координаты вектораdв этом базисе.

Разложение вектора в базисе , имеет вид:=

Переходя к координатам записи, получим:

Решим систему по формуле Крамера:

∆=9

Найдем вспомогательные определители:

,,

Искомое разложение имеет вид: +-

Задание 5. Привести уравнение кривой к каноническому виду. Сделать чертеж. Найти координаты фокусов и вершин. .

Решение.

Выделим полные квадраты по и:

Полученное уравнение - уравнение гиперболы. Центр симметрии в точке 0(0: 3). Действительная полуось гиперболы ; мнимая полуось.

Получим координаты фокусов:

, .

Координаты вершин: ,,,

Рис.3

Задание 6. Дано комплексное число . Записать комплексное число в алгебраической и трибометрической формах. Найти все корни уравнений. Результат изобразить схематически.

Решение.

Запишем комплексное число в алгебраической форме:

Найдем модуль комплексного числа:

Решим уравнение: .

Запишем число zв тригонометрической форме:

По правилу извлечения корня третьей степени из z,получим:

Изобразим схематически полученные результаты.

Алгебраическая форма:

Тригонометрическая форма:

Корни уравнения:

Задание 7. Найти собственные векторы линейного преобразования, приводящего квадратическую формук каноническому виду. Установить вид кривой и сделать чертеж.

Решение.

Составим матрицу квадратной формы:

Найдем собственные значения и собственные векторы линейного преобразования, определяемого матрицей А:

Найдем корни полученного уравнения:

.

Найдем собственные векторы, соответствующие собственным значениям:

Пусть , тогда

Собственный вектор . Найдем единичный вектор: =.

Пусть , тогда.

Собственный вектор = Единичный вектор: =

Составим матрицу преобразования:

Запишем формулы преобразования координат:

Поставим в квадратную форму:

Полученное уравнение описывает гиперболу.

Действительная полуось гиперболы , мнимая полуось.

Сделаем чертеж.

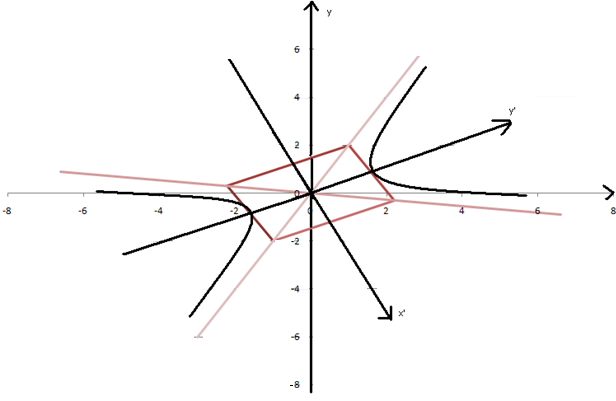
Рис. 5

Содержание

1. Линейные уравнения и неравенства с двумя неизвестными………………….3

2. Системы линейных уравнений и неравенств с двумя неизвестными………..5

3. Матрицы и определители……………………………………………………….7

4. Определители произвольного порядка……………………………………….10

5. Системы линейных алгебраических уравнений……………………………..12

6. Методы решения системы линейных алгебраических уравнений………….14

7. Векторы и линейные операции над ними…………………………………….16

8. Умножение векторов…………………………………………………………...21

9. Комплексные числа…………………………………………………………….24

10. Аналитическая геометрия на плоскости……………………………………..29

11. Различные виды уравнения прямой на плоскости…………………………..30

12. Кривые второго порядка………………………………………………………36

13. Уравнение плоскости………………………………………………………….43

14. Прямая в пространстве………………………………………………………..47

15. Поверхности второго порядка………………………………………………...51

16. Преобразование декартовых координат……………………………………...58

17. Полярная система координат…………………………………………………60

18. Варианты расчётно-графической работы…………………………………….62

19. Пример выполнения расчетно-графической работы………………………..71

80