I. Основные законы движения

Механическое движение. Системы отсчета и системы координат. Понятие материальной точки. Движение материальной точки. Переме­щение, путь, скорость, ускорение, тангенциальная и нормальная составляющие ускорения.

Прочитать § I, 3, 4, § 2 (желательно).

Движение материальной точки по окружности. Связь между векто­рами линейных и угловых скоростей и ускорений (§5).

Инерция, масса, импульс (количество движения), первый закон Нью­тона. Понятие об инерциальных и неинерциальных системах отсчета.

Прочитать § 7, 8, 32.

Сила, второй закон Ньютона (§ 9, 10).

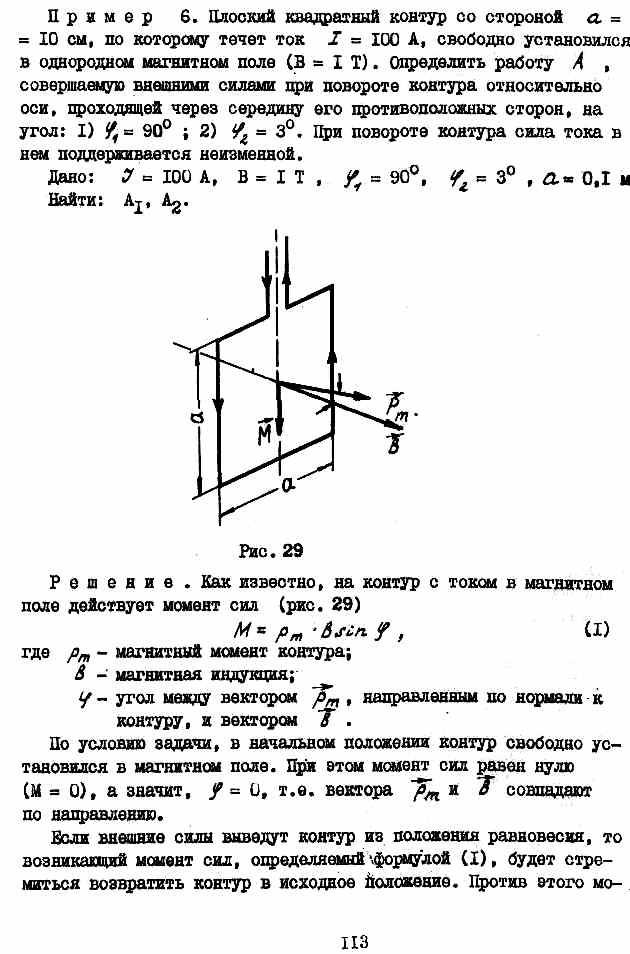
Дополнение. Полезно запомнить следующее определение силы: сила есть мера взаимодействия двух тел (двух объектов). По­этому выражение для любой силы включает в себя характеристики двух тел (объектов). Например,

где f₁ - сила всемирного тяготения между двумя материальными

точками m₁ и m₂, находящимися на расстоянии r ; F₂ - сила взаимодействия двух точечных зарядов q₁ и q₂,

находящихся на расстоянии г ;

F₃ - сила взаимодействия движущихся с относительной ско­ростью V заряда q (один объект) и магнитного поля с индукцией В (второй объект).

Третий закон Ньютона. Механический принцип относительности. Преобразование координат Галилея. Сложение скоростей в классиче­ской механике (§ 11, 12, 17).

2. Законы сохранения

Закон сохранения импульса (§ 18, 27).

Работа и мощность. Работа переменной силы. Кинетическая и по­тенциальная энергия. Закон сохранения энергии в механике. Кон­сервативные и диссипативные системы.

Прочитать § 19, 20 (опустить вывод формул (20.2) и (20.3), § 21, 22, 23 (до формулы (23.11), § 24.

Дополнение. Система тел, подверженная действию лишь консервативных сил (см. определение в § 21), называется консервативной системой. В такой системе выполняется закон сохранения механической энергии. Система тел, подверженная дей­ствию неконсервативных сил (например, силы трения), называется диссипативной системой, ее механическая энергия в общем случае уменьшается во времени из-за перехода в другие формы энергии.

Применение законов сохранения импульса и энергии к упруго­му и неупругому ударам (§28).

3. Твердое тело как система частиц (гл. У)

Понятие абсолютно твердого тела. Поступательное и враща­тельное движение твердого тела. Применимость законов кинемати­ки и динамики материальной точки к поступательному движению твердого тела. Угол поворота, угловая скорость, угловое уско­рение - кинематические характеристики вращательного движения твердого тела (§ 5, 36, 37).

Центр инерции (массы) твердого тела (§ 27),

Вращение твердого тела вокруг неподвижной оси, его момент инерции и кинетическая энергия. Основной закон динамики враща­тельного движения. Закон сохранения момента импульса для сис­темы тел.

Прочитать § 29, 38 (до формулы (38.8); § 39, 41 (до форму­лы (41.I), 42, 43 (желательно).

Дополнение. Поскольку материал, касающийся основ­ного закона динамики вращательного движения, изложен в §. 40 громоздко, ниже предлагается упрощенный вариант его изложения.

Рассмотрим твердое тело, вращающееся вокруг неподвижной оси (рис. I). Очевидно, что сила, действующая вдоль направле­ния, пересекающегося с осью, вокруг этой оси не может вызвать вращения. Также очевидно, что сила, параллельная оси, не вызы­вает относительно нее вращения. Момент силы создается только той составляющей силы, которая лежит в плоскости,_перпендикулярной к оси. Обозначим эту составляющую через F_i. , m_i масса маленького элемента, твердого тела, к которому приложена сила.

Пусть сила F_i образует угол _i с касательной к траекто­рии элемента массой m_i. Тогда для этого элемента можно напи­сать равенство

где F_icos_i=F_ik=m_iw_i- проекция силы F_i , касательная

к траектории элемента m_i ; w_i. - тангенциальное ускорение;

 - угловое ускорение элемента (рис. I).

Такие же равенства мы можем написать для всех прочих эле­ментов, а затем просуммировать их:

угловое ускорение  постоянно для всех элементов, поэтому его можно вынести из под знака суммы:

Величина Nz=F_ikr_i представляет собой сумму моментов сил, действующих на все элементы твердого тела, т.е. она пред­ставляет собой полный момент N_z сил, действующих на твердое тело относительно оси вращения ZZ'. При этом следует произ­ведение F_ikr_i брать со знаком плюс, если точка приложения силы F_i обходит ось в направлении действия силы F_i. , и со знаком минус - в противном случае, величина

равная сумме моментов инерции отдельных элементов, на которые мы разбили тело, называется моментом инерции тела относитель­но данной оси. С учетом выражений для N_z и J_z равенство (I) перепишется следующим образом:

J_z=N_z (2)

Угловое ускорение  , приобретаемое твердым телом: =N_z/J_z

прямо пропорционально приложенному моменту сил N_z и обратно пропорционально моменту инерции J_z. Равенство (2) можно запи­сать в векторной форме:

J_z=N_z. (3)

Сравнивая соотношение (3) с равенством (9.2) (см. гл. II, § 9 [I]), выражающим второй закон Ньютона, мы видим, что для вращения твердого тела вокруг неподвижной оси имеет место со­отношение, вполне аналогичное второму закону Ньютона, только роль линейного ускорения играет угловое ускорение, роль силы -момент силы и роль массы - момент инерции.

Закон сохранения момента импульса также предлагается в нижеследующем изложении, так как материал § 29, посвященный этому вопросу, не очень нагляден.

Рассмотрим первоначально маленький элемент с массой m_i, вращающийся по окружности радиуса r_i (см. рис. I). Для такого элемента имеет место соотношение

F_ik=m_iw_i.

Учитывая, что w_i=v_i/t , это равенство можно переписать следующим образом

F_ikt=m_iv_i .

Умножая правую и левую части этого выражения на r_i , по­лучим

F_ikrit=r_iv_i (4)

или, так как v_i=wr_i, где w - изменение угловой ско­рости твердого тела, то

Суммируя эти выражения для всех i -ых элементов твердого тела получим

или, так как 2SF_ikr_i=N_z - момент сил, действующих на твер­дое тело, a 2Sm_ir²_i=J_z - момент инерции тела, то

Так как момент инерции твердого тела относительно оси Z-Z'-величина постоянная, то это равенство можно переписать в виде

Если момент сил N_z непостоянен, то следует брать диффе­ренциально малый промежуток времени, чтобы N_z можно было счи­тать постоянным. Тогда равенство (6) перепишется следующим об­разом

Выражение (8), записанное в форме

аналогично равенству (9.1) (см. гл. II, § 9 [1]), выражаю­щему связь между скоростью изменения импульса тела и действую­щей на тело силой. Только роль скорости изменения импульса здесь