физика / ЛР ин.-тех. напр / Сборник МУ Часть 3 (нов) / № 35(нов)

36

Лабораторная работа №35

Изучение собственных колебаний крутильного маятника

Цель работы:

1. Изучение основных понятий теории колебаний.

2. Экспериментальная проверка формулы периода собственных колебаний крутильного маятника.

Теоретическое введение

Колебаниями называются процессы, в той или иной степени повторяющиеся во времени.

В зависимости от физической природы колебательного процесса различают механические и электромагнитные колебания. Система, в которой происходят колебания, называется колебательной системой.

Колебания называются свободными (собственными), если они происходят в отсутствие переменных внешних воздействий на колебательную систему. Колебания называются вынужденными, если на систему оказывается периодическое внешнее воздействие.

Колебания называются периодическими, если значения всех физических величин, характеризующих состояние колебательной системы и изменяющихся при ее колебаниях, повторяются через равные промежутки времени. Время, за которое в системе совершается одно полное колебание, называют периодом колебаний (T, с). Величина, равная числу полных колебаний за единицу времени, называется частотой колебаний (ν, Гц):

.

Циклической или круговой частотой называется величина ω, равная:

При периодических колебаниях зависимость колеблющейся величины s от времени t удовлетворяет условию:

.

Периодические колебания называются гармоническими, если колеблющаяся величина меняется с течением времени по закону косинуса или синуса:

или

.

Здесь - циклическая частота колебаний, A – максимальное отклонение колеблющейся величины от положения равновесия (амплитуда колебаний), φ(t) = ωt+φ₀ – фаза колебаний, φ₀ – начальная фаза.

График гармонических колебаний представлен на рисунке 1.

Рисунок 1 – График гармонических колебаний

При гармонических колебаниях полная энергия системы с течением времени не изменяется. Можно показать, что полная энергия механической колебательной системы при гармонических колебаниях равна:

.

Гармонически колеблющаяся величина s(t) подчиняется дифференциальному уравнению:

, (1)

которое называется дифференциальным уравнением гармонических колебаний.

Если какой-либо процесс описывается уравнением такого вида, то этот процесс представляет собой гармоническое колебаний с частотой ω.

Собственные колебания некоторых физических систем при определенных условиях являются близкими к гармоническим. При этом частота собственных колебаний определяется физическими параметрами системы (например, массой груза и упругостью пружины для пружинного маятника). Значения амплитуды и начальной фазы зависят от начальных условий в системе.

Рассмотрим собственные колебания твердого тела, подвешенного вертикально на упругих нитях.

Если повернуть это тело на некоторый угол φ вокруг вертикальной оси и отпустить, то момент упругих сил, возникающий при закручивании нитей подвеса, будет стремиться вернуть тело в исходное положение, и в системе возникнут крутильные колебания. Такую систему называют крутильным маятником.

Запишем основное уравнение динамики вращательного движения для крутильного маятника:

(2)

Здесь М – момент действующих на тело сил, взятых относительно оси вращения; I – момент инерции тела относительно той же оси; - угловое ускорение тела.

При условии, что силы трения в системе пренебрежимо малы, а деформация нитей подвеса является упругой, для определения M можно использовать закон Гука. Для деформации кручения он имеет вид:

где k – коэффициент упругости, φ – угол закручивания нитей подвеса.

С учетом этого уравнение динамики вращательного движения (2) запишется в виде:

Преобразовав это уравнение, получаем:

Сравнив полученное уравнение с уравнением (1), можно сделать вывод о том, что оно представляет собой дифференциальное уравнение гармонических колебаний с циклической частотой:

и периодом:

(3)

Из формулы (3) следует, что период собственных колебаний крутильного маятника определяется коэффициентом упругости нитей подвеса k и моментом инерции вращающегося тела I относительно оси вращения. В данной работе экспериментально исследуется зависимость периода колебаний крутильного маятника от величины его момента инерции.

Моментом инерции материальной точки относительно некоторой оси назы­вается величина, равная произведению массы точки на квадрат ее расстояния от оси:

.

Для протяженных тел момент инерции определяется как сумма моментов инерции отдельных материальных точек (элементарных масс Δm_i), на которые можно разбить тело

.

В предельном случае, когда число элементарных масс стремится к беско­нечности, сумма переходит в интеграл

, (4)

где ρ – плотность, V – объем тела; ρdV – масса бесконечно малого элемента объ­ема dV твердого тела.

Как видно из определения, момент инерции тела есть величина аддитивная; момент инерции тела равен сумме моментов инерции его частей; момент инерции системы тел равен сумме моментов отдельных тел.

Используя формулу (4), можно вывести формулы для моментов инерции часто встречающихся твердых тел правильной геометрической формы массой m.

Так, момент инерции сплошного цилиндра радиуса R относительно оси симмет­рии:

. (5)

Момент инерции шара относительно оси, проходящей через центр шара:

. (6)

Моменты инерции однородного прямоугольного параллелепипеда относительно осей симметрии (см. рисунок 2) равны соответственно:

(7)

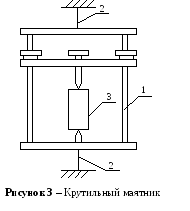
Описание установки и метода

Установка (рисунок 3) представляет собой крутильный маятник и состоит из рамки 1, подвешенной на упругих нитях подвеса 2. В рамку зажимают тело 3, момент инерции которого относительно оси, проходящей через нити подвеса, можно рассчитать, зная его массу и размеры.

Маятник способен совершать крутильные колебания, число n и полное время t которых регистрируются автоматически. Период колебаний можно рассчитать по формуле:

. (8)

Момент инерции маятника относительно оси вращения равен сумме моментов инерции рамки I_P и закрепленного в ней тела I_T:

В соответствии с формулой (3) период собственных колебаний рамки с телом должен быть равен:

. (9)

Для экспериментальной проверки этой формулы измеряют периоды колебаний маятника, поочередно закрепляя в рамке тела с различными моментами инерции I_Т (цилиндр и прямоугольный параллелепипед). Коэффициент жесткости нитей подвеса k и момент инерции рамки I_Р при этом остаются неизменными.

Если возвести обе части выражения (9) в квадрат, то получим:

(10)

График зависимости квадрата периода собственных колебаний T² крутильного маятника от момента инерции I_Т тела, закрепленного в рамке, изображен на рисунке 4. В соответствии с (10) он представляет собой прямую линию, пересекающую ось абсцисс в точке I_Т = - I_Р. Тангенс угла наклона этой прямой к оси абсцисс равен

П орядок выполнения работы

1. Определить массу и размеры используемых в работе тел (цилиндра и прямоугольного параллелепипеда). Результаты занести в таблицу 1.

Таблица 1 - Определение параметров используемых тел

Цилиндр		Прямоугольный параллелепипед
масса m, кг	радиус R, м	масса m, кг	стороны
			a, м	b, м	с, м

2. Рассчитать момент инерции цилиндра относительно оси симметрии по формуле (5) и моменты инерции прямоугольного паралеллелепипеда относительно осей ОХ, ОY и OZ (см. рисунок 2) по формулам (7). Результаты записать в таблицу 2.

3. Закрепить в рамке крутильного маятника цилиндр и измерить время t 10 колебаний кру­тильного маятника. Изме­рения провести 3-5 раз. Данные занести в таблицу 2.

4. Закрепить в рамке прямоугольный параллелепипед так, чтобы ось вращения совпадала с осью OX. Измерить время 10 крутильных колебаний. Измерения провести 3-5 раз. Данные занести в таблицу 2.

5. Повторить п.4, закрепляя в рамке прямоугольный параллелепипед так, чтобы ось вращения сначала совпала с осью OY, а затем с осью OZ.

Таблица 2 – Измерение периодов колебаний крутильного маятника

Тело	Ось вращения	n	t1, c	t2, c	t3, c	<t>, c	T = <t>/n, c	Т2, с2	IТ, кг · м2
Цилиндр	ось симметрии	10
Паралле-лепипед	ОХ	10
	OY	10
	OZ	10

Обработка результатов измерений

1. Рассчитать средние значения времени 10 колебаний <t> , периоды колебаний T , а также их квадраты T² для всех строк таблицы 2._.

2. Построить график зависимости T² от I_Т . Сделать вывод о справедливости формулы периода собственных колебаний крутильного маятника.

Примечание: Пункты 3 и 4 выполняются по указанию преподавателя.

3. Продолжив полученный график до пересечения с осью абсцисс (см. рис.4), найти момент инерции рамки крутильного маятника I_Р .

4. Определить коэффициент жесткости нитей подвеса крутильного маятника по формуле:

Контрольные вопросы

1. Что такое колебания? Дайте определение собственных и вынужденных колебаний.

2. Какие колебания называются гармоническими? Запишите уравнение гармонических колебаний. Дайте определения основных характеристик гармонических колебаний (амплитуды, частоты, циклической частоты, периода, фазы, начальной фазы).

3. Нарисуйте график гармонических колебаний.

4. Запишите дифференциальное уравнение гармонических колебаний.

5. Что такое крутильный маятник? При каких условиях колебания крутильного маятника близки к гармоническим?

6. Используя основное уравнение вращательного движения, выведите формулу для периода собственных колебаний крутильного маятника.

7. Как зависит период колебаний от момента инерции маятника и коэффициента жесткости нитей подвеса?

8. Как проверяется в лабораторной работе справедливость формулы периода собственных колебаний крутильного маятника?

9. Как можно в данной работе экспериментально определить момент инерции рамки и коэффициент жесткости нитей подвеса крутильного маятника?

Список рекомендуемой литературы

1. Трофимова, Т.И. Курс физики: учеб. пособие для инженер.-техн. специальностей вузов / Т. И. Трофимова. - 13-е изд., стер. - М.: Академия, 2007. – §§ 140-142.

2. Детлаф, А.А. Курс физики: учеб. пособие для втузов / А. А. Детлаф, Б. М. Яворский. - 7-е изд., стер. - М.: Академия, 2008. - § 27.1.

3. Грабовский, Р.И. Курс физики: учеб. пособие для вузов по естественнонауч., техн. и с.-х. направлениям и специальностям / Р. И. Грабовский. - 10-е изд., стер. - СПб.: Лань, 2007. - §§ 27, 29.