18

Лабораторная работа № ксе-01

ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ И КОСВЕННЫХ ИЗМЕРЕНИЙ

НА ПРИМЕРЕ ИЗМЕРЕНИЯ ПЛОТНОСТИ

Цель работы:

1. Ознакомиться с основными понятиями теории погрешностей и методами обработки результатов измерений.

2. Определить плотность тела правильной геометрической формы с учетом погрешности.

Теоретическое введение

Основные понятия и термины

Одним из основных эмпирических методов естествознания является измерение – то есть определение количественного значения какой-либо величины путем ее сопоставления (непосредственного или косвенного) с эталоном. Как правило, абсолютно точные измерения невозможны. Действительно, для абсолютно точных измерений нужно, во-первых, иметь абсолютно точный измерительный прибор, во-вторых, полностью исключить влияние в ходе измерений внешних неконтролируемых факторов на измерительный прибор и на сам исследуемый объект. Оба эти условия на практике невыполнимы. Поэтому задачей измерений является не нахождение точного значения интересующей нас величины, а нахождение так называемого доверительного интервала и минимизация возникающей при измерении погрешности.

Доверительный интервал – интервал, в котором с заданной, так называемой доверительной вероятностью  находится истинное значение искомой величины (рисунок 1.1). Результат нахождения доверительного интервала должен быть представлен следующим образом:

, (1.1)

где – среднее значение результата измерений;

ΔА – полуширина доверительного интервала или, иначе говоря, абсолютная погрешность измерений;

– доверительная вероятность.

При этом необходимо учитывать, что численное значение ΔА должно содержать не более двух значащих цифр, а значение должно оканчиваться цифрой того же разряда, что и ΔА.

Например, результат измерения времени движения тела имеет вид

t = (18,5 ± 1,2) c; = 0,95.

Из этой записи следует, что с вероятностью 95 % истинное значение времени движения лежит в интервале от 17,3 с до 19,7 с.

Отметим, что величина абсолютной погрешности не является мерой точности выполненного измерения. Допустим, при измерении расстояния была допущена абсолютная погрешность 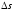= 1 км. Много это или мало? Это может быть и много, если само измеряемое расстояние равно нескольким километрам, и очень мало, если измерялось огромное расстояние, например расстояние от Земли до Луны. Мерой точности измерения являетсяотносительная погрешность, показывающая соотношение между абсолютной погрешностью и средним значением измеряемой величины:

. (1.2)

Иногда относительную погрешность выражают в процентах

. (1.2а)

Измерения подразделяются на прямые и косвенные. При прямом измерении значение искомой величины определяется непосредственно с помощью прибора, предназначенного для измерения именно этой величины (измерение длины образца линейкой, длительности процесса с помощью часов и т.п.). При косвенном измерении искомая величина находится (вычисляется) по некоторой известной формуле на основании прямых или косвенных измерений величин, входящих в эту формулу. Например, для определения плотности  однородного материала можно использовать формулу

, (1.3)

где m – масса тела, которую можно измерить прямо, например с помощью весов;

V – объем тела.

Объем может быть измерен прямо, например, с помощью мерного стакана, но для тел правильной геометрической формы зачастую (и в данной работе также) его находят косвенно, то есть вычисляют по формуле на основании прямых измерений размеров тела. В данной работе используется тело (брусок) в форме прямоугольного параллелепипеда и его объем находится по формуле

V=a·b·c, (1.4)

где a, b, c – длина, ширина и высота бруска, измеряемые прямо с помощью штангенциркуля.

Отклонение результата прямого или косвенного измерения от истинного значения искомой величины называется погрешностью измерения. Погрешности прямых измерений обусловлены возможностями измерительных приборов, методикой измерений и условиями проведения эксперимента. Погрешности косвенных измерений обусловлены “переносом” на искомую величину погрешностей прямых измерений тех величин, на основе которых она рассчитывается. Существуют погрешности трех видов: систематические, случайные и промахи.

Под систематическими погрешностями понимают те, причина возникновения которых остается постоянной или закономерно изменяется в течение всего процесса измерения. Если причина систематической погрешности постоянна, то такая погрешность воспроизводится при повторных измерениях и поэтому не может быть обнаружена и устранена путем многократных измерений. Источниками систематических погрешностей обычно являются неправильная юстировка приборов, закономерно изменяющиеся внешние факторы, неправильно выбранная методика измерений. Для выявления и исключения систематических погрешностей необходимо предварительно проанализировать условия измерения, провести контрольные поверки измерительных приборов и сопоставить получаемые результаты с данными более точных измерений. К неисключаемым систематическим погрешностям, которые необходимо учитывать при обработке результатов, относят погрешности используемых приборов и инструментов (приборные погрешности).

Приборная погрешность для приборов типа линейки, штангенциркуля, микрометра равна половине цены деления прибора

, (1.5)

для стрелочных электроизмерительных приборов определяется по классу точности прибора.

Под классом точности прибора γ понимают величину, равную:

, (1.6)

где ΔA_пр  приборная погрешность, одинаковая для всех точек шкалы;

A_max  предел измерения (максимальное значение показаний прибора).

Для электронных приборов формулы для расчета приборной погрешности приводятся в паспорте прибора.

Случайные погрешности возникают в результате действия различных случайных факторов. Этот вид погрешностей обнаруживается при многократном измерении одной и той же величины в одинаковых условиях с помощью одних и тех же приборов: результаты серии измерений несколько отличаются друг от друга случайным образом. Вклад случайных погрешностей в результат измерения учитывают и минимизируют путем многократных измерений и последующей обработки результатов.

Под промахами понимают большие погрешности, резко искажающие результат измерения. Они возникают как следствие грубых нарушений процесса измерений: неисправности приборов, ошибок экспериментатора, скачков напряжения в электрической цепи и т.д. Результат измерений при промахе резко отличается от результатов повторных измерений и должен быть отброшен в процессе предварительного анализа.

С целью выявления промахов и учета вклада случайных и приборных погрешностей прямые измерения искомой величины проводят несколько раз в одних и тех же условиях, то есть проводят серию равноточных прямых измерений. Целью последующей обработки результатов серии равноточных измерений является нахождение доверительного интервала, то есть:

– получение значения искомой величины, наиболее близкого к истинному (среднего значения серии измерений);

– определение полуширины доверительного интервала.