§15. Преобразование декартовых координат.
Известно, что положение точки М некоторого пространства Vможно однозначно определить, задав координатыx,yиzэтой точки относительно некоторой системы координатOXYZ. Выбор системы координат – произвольный. Очевидно, что в одной системе координатXOYZточка М будет иметь координаты М(x;y;z), а в другой системеX’O’Y’Z’ точка М будет иметь другие координаты М(x’;y’;z’). Естественно возникает задача: зная координаты точки М в одной системе координат, выразить через них координаты той же точки М относительно другой системы.
Задача сводится к нахождению трех функций:
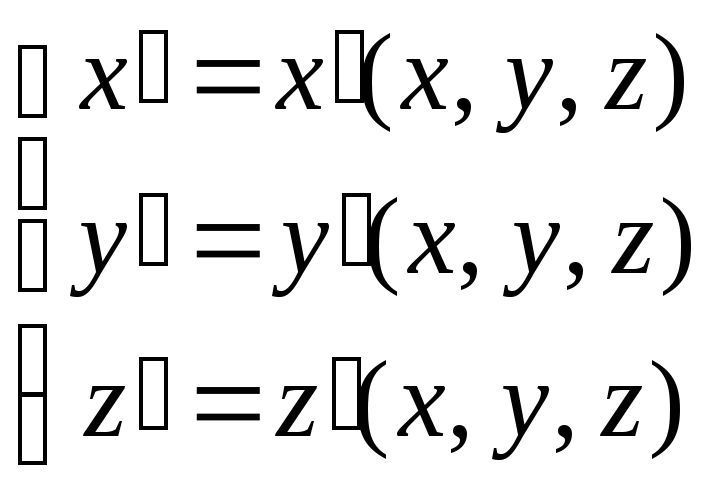
позволяющих однозначно определить координаты точки М относительно одной системы координат, зная их относительно другой системы. Если системы XOYZиX’O’Y’Z’ - прямоугольные декартовы системы координат, то формулы перехода от одной системы координат к другой системе имеют вид:
где точка
- начало координат новой системыX’O’Y’Z’;
- направляющие косинусы углов, составленных
единичными векторами новой и старой
систем координат. Если система координат
определена на плоскости, то формулы
преобразования имеют вид:
.
Если
,
то есть начало новой системы координат
совпадает с началом старой системы, то
формулы преобразования имеют вид:
и определяют поворот системы.
Если единичные векторы старой и новой систем коллинеарны, то получим преобразование параллельного переноса:
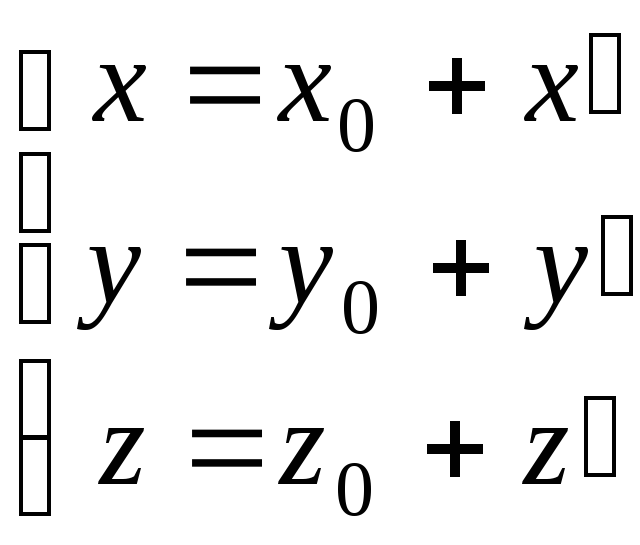
На плоскости преобразования поворота
и параллельного переноса имеют вид:
Общее преобразование можно рассматривать как суперпозицию параллельного переноса и поворота системы координат. Справедливо фундаментальное утверждение: каковы бы ни были две произвольные прямоугольные декартовы системы координат, координаты x,y,zлюбой точки пространства относительно одной системы являются линейными функциями координатx’,y’,z’ той же точки относительно другой системы.
§16. Кривые и поверхности второго порядка.
Поверхностью второго порядка называют совокупность точек пространства, координаты которых x,y,zудовлетворяют уравнению
Коэффициенты
могут принимать любые действительные
значения и удовлетворяют условию
.
Для определения вида поверхности второго порядка необходимо ее уравнение привести к виду, не содержащему произведений координат. Этого можно достичь соответствующим выбором системы координат.
называют квадратичной формой. Матрицу
,
где
,
называют матрицей квадратичной формы.
Вектор
,
удовлетворяющий условию
называют собственным вектором матрицы
А,
- собственным значением.
Каждая матрица квадратичной формы имеет три взаимно ортогональных собственных вектора. Если единичные векторы собственных векторов матрицы А принять за единичные векторы новой системы координат, то в выражении квадратичной формы коэффициенты при произведениях обратятся в ноль и форма примет вид:
.
Присоединяя к ней линейную часть общего уравнения поверхности второго порядка и выделяя полные квадраты, получим каноническое уравнение поверхности второго порядка.
Преобразование уравнения линии второго порядка проводят аналогично. Рассмотрим пример.
Пример 24.Привести к каноническому виду уравнение кривой второго порядка и сделать чертёж:
17x2+8y2+12xy+10x– 8y+ 5 = 0.
Решение.
Составим матрицу квадратичной формы:
.
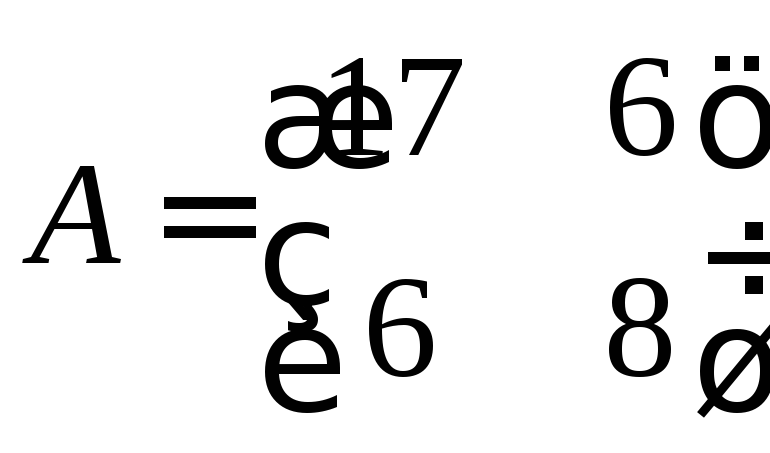Найдем собственные векторы линейного преобразования из условия:
.
Полученная система однородная. Она имеет ненулевые решения, если определитель системы равен нулю:
,
Отсюда находим:
.
Найдём собственные векторы.
При
получим систему уравнений:
Полагая
,
найдём
.
Получим первый собственный вектор
.
При
получим систему уравнений:
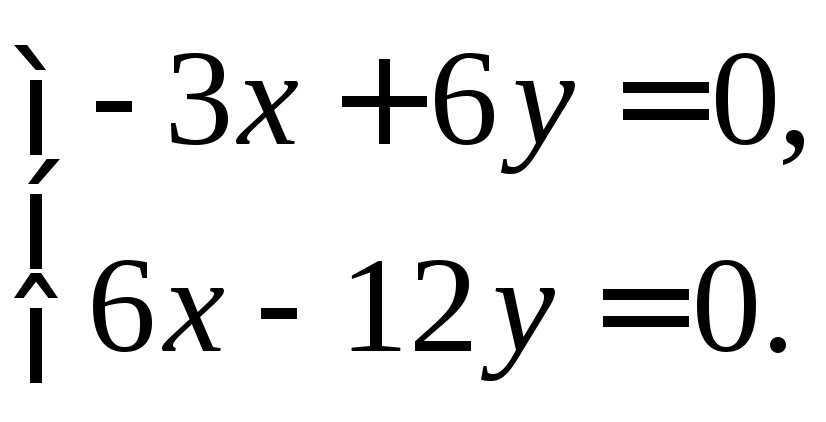
Откуда
,
.
Получим второй собственный вектор
.
Найдём орты собственных векторов.
,
Запишем матрицу преобразования:
Формулы линейного преобразования примут вид:
или
.
Подставим значения
и
в уравнение кривой:
или
Выделяя полные квадраты, получим:
.
Введём новые координаты:
Совершив параллельный перенос осей координат и разделив на 5 обе части уравнения, получим каноническое уравнение:
Это уравнение описывает эллипс, полуоси
которого
.
Построим эллипс по полученному уравнению.
Классификация поверхностей второго порядка.
Применяя преобразование координат, уравнение поверхности второго порядка всегда можно привести к виду:
.
В зависимости от величины и знаков
коэффициентов
,
,
,
,
,
и
могут представиться следующие частные
случаи уравнений поверхностей второго
порядка.
Таблица 1.
1. Эллипсоиды:
трехосный эллипсоид,
мнимый эллипсоид
точка
2
.
Гиперболоиды:
1)
однополостные
гиперболоиды
2
)
двуполостные
гиперболоиды
3. Конусы:
4. Параболоиды:
1
)
эллиптические параболоиды
2
)
гиперболические параболоиды
5. Цилиндры
1)
эллиптические цилиндры
2
)
гиперболические цилиндры
3
)
- параболические цилиндры
6.
Пары плоскостей:
1)
- пары пересекающихся плоскостей
2
)
- пары параллельных плоскостей
3
)
- пары совпадающих плоскостей
