К.Р. №3,4 (заочное)Word

Контрольная работа №3

Задание 1. Дана функция z = f(x,y), найти:1) полный дифференциал dz; 2) частные производные второго порядка , ,, .

1. . 2. . 3. . 4.. 5..

6. . Показать, что

7. . Показать, что

8. . Показать, что

9. . Показать, что

10. . Показать, что

Задание 2. Исследовать функцию на экстремум.

1. 2. .

3. 4. .

5. 6. .

7. 8.

9. 10.

Задание 3. Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям.

1. 2.

3. 4.

5. 6.

7. 8.

9. 10.

Задание 4. Даны линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Найти частное решение, удовлетворяющее указанным начальным условиям.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

Контрольная работа №4

Задание 1. Заданы функция предложения некоторого товара S=S(p) и функция спроса q=q(p) относительно цены p. Определить цену равновесия, т.е. цену, при которой спрос и предложение уравновешиваются, а также эластичность спроса и предложения для этой цены. Построить графики S=S(p) и q=q(p). Как изменится цена при увеличении предложения на 0,2%? Как изменится цена при увеличении спроса на 0,3%?

1. 2.

3. 4.

5. 6.

7. 8.

9. 10.

Задание 2. Исследовать сходимость числового ряда .

1. . 2.. 3.. 4. .

5. . 6.. 7..

8. . 9. . 10. .

Задание 3. Найти интервал сходимости степенного ряда .

1. . 2. . 3. . 4. .

5. 6. . 7. . 8. .

9. . 10. .

Задание 4. Использование дифференциальных уравнений в экономической динамике

1. Функция спроса и (соответственно) предложения имеют вид:

.

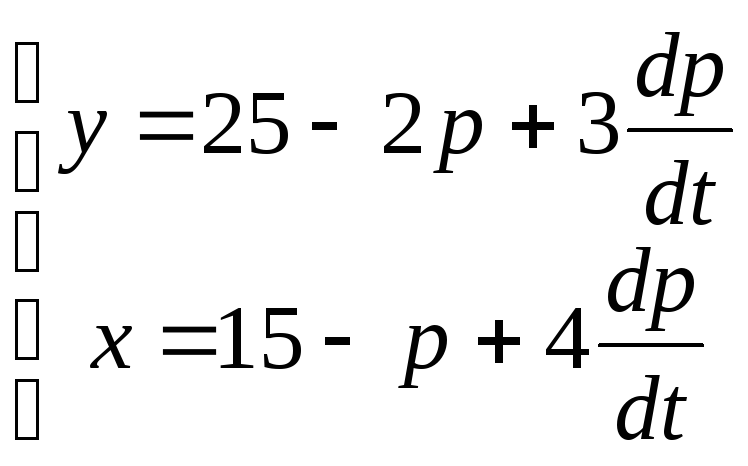Найти зависимость равновесной цены от времени, если в начальный момент .

2. Функция спроса и (соответственно) предложения имеют вид:

.

Найти зависимость равновесной цены от времени, если . Является ли равновесная цена устойчивой?

3. Функция спроса и (соответственно) предложения имеют вид:

.

Найти зависимость равновесной цены от времени, если . Является ли равновесная цена устойчивой?

4. Предполагая, что цена на товар задается функцией ,, , , найти зависимость объема реализованной продукции от времени.

5. Известно, что рост числа жителей некоторого района описывается уравнением:

,

где - максимально возможное число жителей для данного района. В начальный момент времени число жителей составило 1% от максимального. Через какой промежуток времени число жителей составит 80% от максимального?

6. Найти выражение объема реализованной продукции и его значение при , если известно, что кривая спроса имеет вид , норма акселерации , норма инвестиций , .

7. Найти функцию дохода , если известно, что величина потребления задается функцией 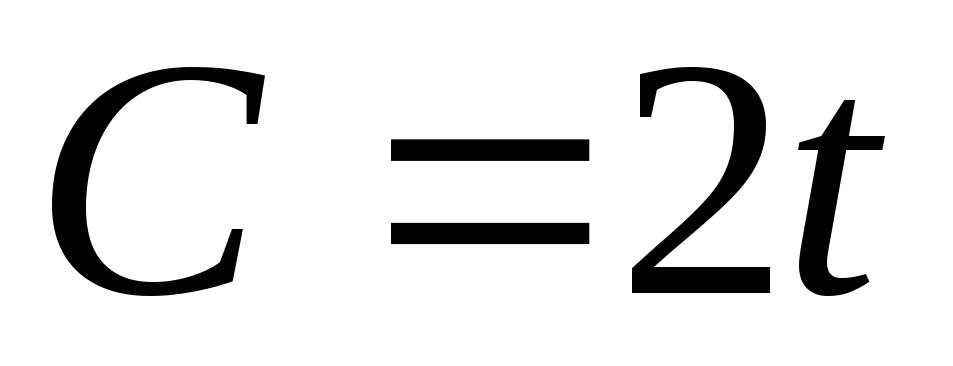; коэффициент капиталоемкости прироста дохода , .

8. В поселке с населением 3000 человек распространение эпидемии гриппа (без применения экстренных санитарно-профилактических мер) описывается уравнением:

,

где - число заболевших в момент времени ; - число недель. Сколько больных будет в поселке через две недели, если в начальный момент было трое больных?

9. Найти выражение объема реализованной продукции , если известно, что кривая спроса имеет вид , норма акселерации , норма инвестиций , .

10. За 30 дней распалось 50% первоначального количества радиоактивного вещества. Через сколько времени останется 1% первоначального количества?

Указание. Использовать закон радиоактивного распада: количество радиоактивного вещества, распадающегося за единицу времени, пропорционально количеству вещества, имеющегося в рассматриваемый период.