
- •Вопрос 1.
- •Вопрос 2
- •Вопрос 3
- •Вопрос 4
- •Вопрос 5
- •Вопрос 6
- •Вопрос 7
- •Вопрос 8
- •Вопрос 9
- •Вопрос 10
- •Вопрос 12
- •Вопрос 13
- •Вопрос 14
- •Вопрос 15
- •Вопрос 16
- •Вопрос 17
- •Вопрос 18
- •Вопрос 19
- •Вопрос 20
- •Вопрос 21
- •Вопрос 22
- •Вопрос 23
- •Где — гамма-функцияЭйлера. Свойства распределения Стьюдента Распределение Стьюдента симметрично. В частности если , то .
- •Вопрос 24
- •Вопрос 25
- •Вопрос 26
- •Вопрос 27
- •Вопрос 28
- •Вопрос 29
- •Вопрос 30
- •Вопрос 31.
- •Вопрос 32
- •Вопрос 33
- •Вопрос 34
- •Вопрос 35
- •Вопрос 36
- •Вопрос 37
- •Вопрос 39
- •Вопрос 40
- •Вопрос 41
- •Вопрос 42
- •Вопрос 43
- •Вопрос 44
- •Вопрос 45
- •Вопрос 46
- •Вопрос 47
- •Вопрос 48
- •Вопрос 49
- •Вопрос 50
- •Вопрос 51
- •Вопрос 52
- •Вопрос 53
- •Вопрос 54
- •Вопрос 55
- •Вопрос 56
- •Вопрос 57
- •Вопрос 58
- •Вопрос 59
- •Вопрос 60
- •Вопрос 61
- •Вопрос 62
- •Вопрос 63
- •Вопрос 64
- •Вопрос 65
- •Вопрос 66
- •Вопрос 68
- •Вопрос 69Связь между мощностью физической дозы р (в мкр/сек) и γ-активностью точесчного источника m, выраженной в миллиграмм-эквивалентах радия:
- •Вопрос 70
- •Вопрос 71
- •Вопрос 72
- •Вопрос 73
- •Вопрос 74
- •Вопрос 75
- •Вопрос 76
- •Вопрос 77
Вопрос 22
Доверительная
вероятность.Надежностью (доверительной
вероятностью) оценки
по статистической оценке *
называется вероятность
![]() ,
с которой осуществляется неравенство
,
с которой осуществляется неравенство
![]() Обычно надежность оценки задается
наперед, причем в качестве
Обычно надежность оценки задается
наперед, причем в качестве
![]() берут число, близкое к единице. Наиболее
часто задают надежность, равную 0,95; 0,99
и 0,999. Пусть вероятность того, что
берут число, близкое к единице. Наиболее
часто задают надежность, равную 0,95; 0,99
и 0,999. Пусть вероятность того, что
![]() равна
равна
![]() :
:![]() .
Заменив неравенство
.
Заменив неравенство
![]() равносильным ему двойным неравенством
равносильным ему двойным неравенством
![]() или
или
![]() ,
имеем
,
имеем
![]() .Это
соотношение следует понимать так:
вероятность того, что интервал
.Это
соотношение следует понимать так:
вероятность того, что интервал
![]() заключает в себе (покрывает) неизвестный
параметр
заключает в себе (покрывает) неизвестный
параметр
![]() ,
равна
,
равна
![]() .
Доверительным называют интервал
.
Доверительным называют интервал
![]() ,
который покрывает неизвестный параметр
с заданной надежностью
,
который покрывает неизвестный параметр
с заданной надежностью
![]() .
.
Доверительный
интервал. Пусть
![]() - выборка из генеральной совокупности
объема
- выборка из генеральной совокупности
объема
![]() ,
,
![]() - выборочное среднее,
- выборочное среднее,
![]() - выборочная дисперсия,
- выборочная дисперсия,
![]() - выборочное среднее квадратическое
отклонение,
- выборочное среднее квадратическое
отклонение,
![]() -
выборочная доля признака. Доверительный
интервал уровня надежности
-
выборочная доля признака. Доверительный
интервал уровня надежности
![]() для генеральной средней
для генеральной средней
![]() имеет вид
имеет вид
![]() ,
где
,
где
![]() - предельная ошибка выборки, зависящая
от
- предельная ошибка выборки, зависящая
от
![]() .
При
.
При
![]() для повторной выборки
для повторной выборки![]() ,а
для бесповторной выборки
,а
для бесповторной выборки
![]() .
Здесь
.
Здесь
![]() определяется из условия
определяется из условия![]() ,где
,где
![]() - функция Лапласа. Если
- функция Лапласа. Если
![]() ,
то доверительный интервал для
,
то доверительный интервал для
![]() строится только для нормальной генеральной
совокупности. Для повторной выборки
строится только для нормальной генеральной
совокупности. Для повторной выборки
![]()
Вопрос 23
Распределе́ние
Стью́дента в
теории
вероятностей— это однопараметрическое
семействоабсолютно
непрерывных распределенийПусть
![]() —
независимыестандартные
нормальныеслучайные
величины, такие что
—
независимыестандартные
нормальныеслучайные
величины, такие что
![]() .
Тогда распределениеслучайной величины
.
Тогда распределениеслучайной величины
![]() ,
где
,
где
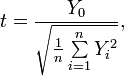
называется
распределением Стьюдента с
![]() степенями
свободы. Пишут
степенями
свободы. Пишут
![]() .
Её распределение абсолютно непрерывно
и имеет плотность
.
Её распределение абсолютно непрерывно
и имеет плотность
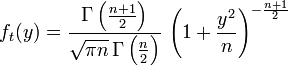 ,
,
Где — гамма-функцияЭйлера. Свойства распределения Стьюдента Распределение Стьюдента симметрично. В частности если , то .
Вопрос 24
Погрешность
измерения —
оценкаотклоненияизмеренногозначения величины от её истинного
значения. Погрешность измерения является
характеристикой (мерой)точностиизмерения.По
форме представления: Абсолютная
погрешность —
![]() является
оценкой абсолютной ошибки измерения.
Величина этой погрешности зависит от
способа её вычисления, который, в свою
очередь, определяется распределением
случайной величины
является
оценкой абсолютной ошибки измерения.
Величина этой погрешности зависит от
способа её вычисления, который, в свою
очередь, определяется распределением
случайной величины
![]() .
При этом неравенство:
.
При этом неравенство:
![]() ,
где
,
где
![]() —
истинное значение, а
—
истинное значение, а
![]() —
измеренное значение, должно выполняться
с некоторой вероятностью, близкой к 1.
Если случайная величина
—
измеренное значение, должно выполняться
с некоторой вероятностью, близкой к 1.
Если случайная величина
![]() распределена
по нормальному
закону, то обычно за абсолютную
погрешность принимают еёсреднеквадратичное
отклонение.Абсолютная
погрешностьизмеряется в тех же
единицах измерения, что и сама величина.
Вид записи:9,930±0,005
с. Или
1,380 6488×10−23±0,000 0013×10−23
Дж/К.
Относительная погрешность —
погрешность измерения, выраженная
отношением абсолютной погрешности
измерения к действительному или
измеренному значению измеряемой величины
(РМГ 29-99):
распределена
по нормальному
закону, то обычно за абсолютную
погрешность принимают еёсреднеквадратичное
отклонение.Абсолютная
погрешностьизмеряется в тех же
единицах измерения, что и сама величина.
Вид записи:9,930±0,005
с. Или
1,380 6488×10−23±0,000 0013×10−23
Дж/К.
Относительная погрешность —
погрешность измерения, выраженная
отношением абсолютной погрешности
измерения к действительному или
измеренному значению измеряемой величины
(РМГ 29-99):
![]() ,
,
![]() .
Относительная погрешность является
безразмерной величиной, либо измеряется
в процентах.Приведённая
погрешность —
погрешность, выраженная отношением
абсолютной погрешности средства
измерений к условно принятому значению
величины, постоянному во всем диапазоне
измерений или в части диапазона.
Вычисляется по формуле
.
Относительная погрешность является
безразмерной величиной, либо измеряется
в процентах.Приведённая
погрешность —
погрешность, выраженная отношением
абсолютной погрешности средства
измерений к условно принятому значению
величины, постоянному во всем диапазоне
измерений или в части диапазона.
Вычисляется по формуле
![]() ,
где
,
где
![]() —
нормирующее значение, которое зависит
от типа шкалы измерительного прибора
и определяется по его градуировке:1)если
шкала прибора односторонняя, то есть
нижний предел измерений равен нулю, то
—
нормирующее значение, которое зависит
от типа шкалы измерительного прибора
и определяется по его градуировке:1)если
шкала прибора односторонняя, то есть
нижний предел измерений равен нулю, то
![]() определяется
равным верхнему пределу измерений;
2)если шкала прибора двухсторонняя, то
нормирующее значение равно ширине
диапазона измерений прибора.Приведённая
погрешность является безразмерной
величиной, либо измеряется в процентах.
По причине возникновения:Инструментальные
/ приборные погрешности —
погрешности, которые определяются
погрешностями применяемых средств
измеренийи вызываются несовершенством
принципа действия, неточностьюградуировкишкалы,
ненаглядностью прибора.Методические
погрешности —
погрешности, обусловленные несовершенством
метода, а также упрощениями, положенными
в основу методики.Субъективные
/ операторные / личные погрешности —
погрешности, обусловленные степенью
внимательности, сосредоточенности,
подготовленности и другими качествами
оператора.По
характеру проявления Случайная
погрешность —
составляющая погрешности измерения,
изменяющаяся случайным образом в серии
повторных измерений одной и той же
величины, проведенных в одних и тех же
условиях. В появлении таких погрешностей
не наблюдается какой-либо закономерности,
они обнаруживаются при повторных
измерениях одной и той же величин
Систематическая
погрешность —
погрешность, изменяющаяся во времени
по определённому закону (частным случаем
является постоянная погрешность, не
изменяющаяся с течением времени).
Систематические погрешности могут быть
связаны с ошибками приборов (неправильная
шкала, калибровка и т. п.), неучтёнными
экспериментатором. Систематическую
ошибку нельзя устранить повторными
измерениями. С.о. устраняют либо с помощью
поправок или «улучшением» эксперимента.
Прогрессирующая
(дрейфовая) погрешность —
непредсказуемая погрешность, медленно
меняющаяся во времени. Она представляет
собой нестационарный случайный процесс.
Грубая погрешность
(промах) —
погрешность, возникшая вследствие
недосмотра экспериментатора или
неисправности аппаратуры (например,
если экспериментатор неправильно прочёл
номер деления на шкале прибора или если
произошло замыкание в электрической
цепи).
определяется
равным верхнему пределу измерений;
2)если шкала прибора двухсторонняя, то
нормирующее значение равно ширине
диапазона измерений прибора.Приведённая
погрешность является безразмерной
величиной, либо измеряется в процентах.
По причине возникновения:Инструментальные
/ приборные погрешности —
погрешности, которые определяются
погрешностями применяемых средств
измеренийи вызываются несовершенством
принципа действия, неточностьюградуировкишкалы,
ненаглядностью прибора.Методические
погрешности —
погрешности, обусловленные несовершенством
метода, а также упрощениями, положенными
в основу методики.Субъективные
/ операторные / личные погрешности —
погрешности, обусловленные степенью
внимательности, сосредоточенности,
подготовленности и другими качествами
оператора.По
характеру проявления Случайная
погрешность —
составляющая погрешности измерения,
изменяющаяся случайным образом в серии
повторных измерений одной и той же
величины, проведенных в одних и тех же
условиях. В появлении таких погрешностей
не наблюдается какой-либо закономерности,
они обнаруживаются при повторных
измерениях одной и той же величин
Систематическая
погрешность —
погрешность, изменяющаяся во времени
по определённому закону (частным случаем
является постоянная погрешность, не
изменяющаяся с течением времени).
Систематические погрешности могут быть
связаны с ошибками приборов (неправильная
шкала, калибровка и т. п.), неучтёнными
экспериментатором. Систематическую
ошибку нельзя устранить повторными
измерениями. С.о. устраняют либо с помощью
поправок или «улучшением» эксперимента.
Прогрессирующая
(дрейфовая) погрешность —
непредсказуемая погрешность, медленно
меняющаяся во времени. Она представляет
собой нестационарный случайный процесс.
Грубая погрешность
(промах) —
погрешность, возникшая вследствие
недосмотра экспериментатора или
неисправности аппаратуры (например,
если экспериментатор неправильно прочёл
номер деления на шкале прибора или если
произошло замыкание в электрической
цепи).
