2.5. Нормальный закон распределения случайных величин

Нормальный закон распределения (закон Гаусса) играет исключительно важную роль в теории вероятностей. Во-первых, это наиболее часто встречающийся на практике закон распределения непрерывных случайных величин. Во-вторых, он является предельным законом в том смысле, что к нему при определенных условиях приближаются другие законы распределения.

Нормальный закон распределения характеризуется следующей формулой для плотности вероятности:

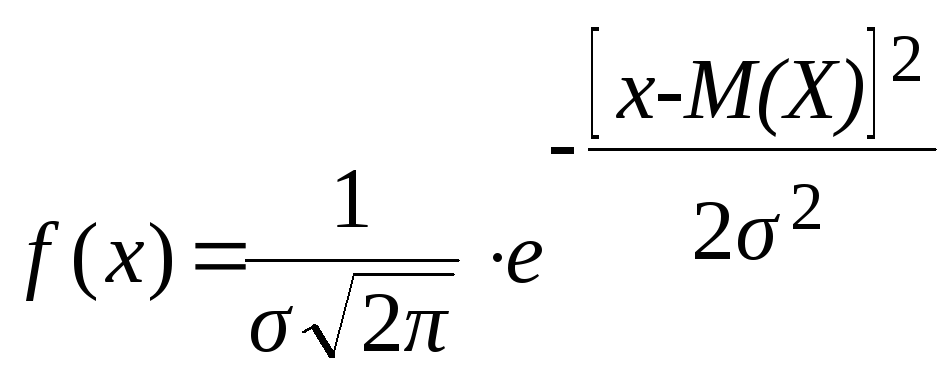, (26)

где х – текущие значения случайной величины X; М(X) и  – ее математическое ожидание и стандартное отклонение. Из (26) видно, что если случайная величина распределена по нормальному закону, то достаточно знать только два числовых параметра: М(Х) и , чтобы полностью знать закон ее распределения.

График функции (26) называется нормальной кривой распределения (кривой Гаусса). Он имеет симметричный вид относительно ординатых = М(Х). Максимальная плотность вероятности, равная  , соответствует математическому ожиданиюМ(Х) = ; по мере удаления от нее плотность вероятности f(х) падает и постепенно приближается к нулю (рис. 5).

Величина М(Х) называется также центром рассеяния. Среднеквадратичное отклонение  характеризует ширину кривой распределения.

При изменении значенияМ(Х) в (26) нормальная кривая не меняется по форме, но сдвигается вдоль оси абсцисс. С возрастанием  максимальная ордината кривой убывает, а сама кривая, становясь более пологой, растягивается вдоль оси абсцисс, при уменьшении  кривая вытягивается вверх, одновременно сжимаясь с боков. Вид кривой распределения при разных значениях :(₃<₂<₁) показан на рис.6.

Естественно, что при любых значениях М(Х) и  площадь, ограниченная нормальной кривой и осью Х, остается равной 1 (условие нормировки):

f(х) dх = 1, или f(х) dх = 1.

Нормальное распределение симметрично, поэтому М(Х) = Мо(Х) = Ме(Х).

Вероятность попадания значений случайной величины Х в интервал (x₁,x₂), т.е. Р (x₁ < Х< x₂), равна:

Р(x₁ < Х < x₂) =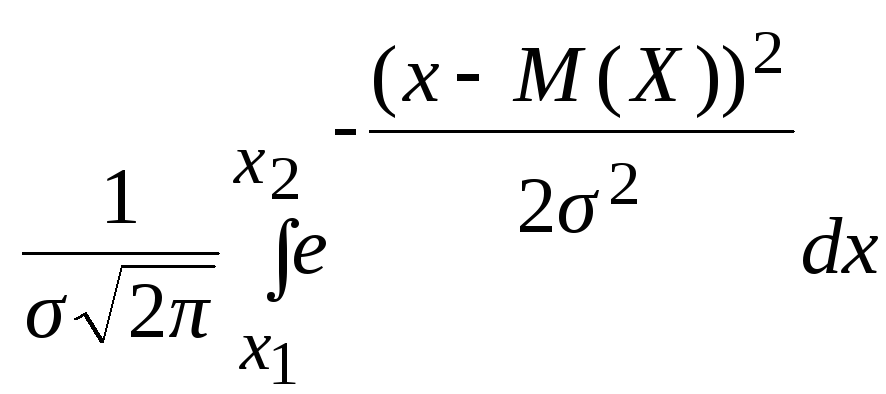 . (27)

На практике часто приходиться вычислять вероятности попадания значений нормально распределенной случайной величины на участки, симметричные относительноМ(Х). В частности, рассмотрим следующую, важную в прикладном отношении задачу. Отложим от М(Х) вправо и влево отрезки, равные , 2 и 3 (рис. 7) и проанализируем результат вычисления вероятности попадания Х в соответствующие интервалы:

Р(М(Х) –  <Х<М(Х) + ) = 0,6827 = 68,27 %. (28)

Р(М(Х) – 2 <Х<М(Х) + 2) = 0,9545 = 95,45 %. (29)

Р(М(Х) – 3 <Х<М(Х) + 3) = 0,9973 = 99,73 %. (30)

Из (30) следует: практически достоверно, что значения нормально распределенной случайной величины Х с параметрами М(Х) и  лежат в интервале М(Х)  3. Иначе говоря, зная М(Х) = и, можно указать интервал, в который с вероятностью Р = 99,73% попадают значения данной случайной величины. Такой способ оценки диапазона возможных значений Х известен как «правило трех сигм».

Пример. Известно, что для здорового человека рН крови является нормально распределенной величиной со средним значением (математическим ожиданием) 7,4 и стандартным отклонением 0,2. Определите диапазон значений этого параметра.

Решение: для ответа на этот вопрос воспользуемся “правилом трех сигм”. С вероятностью равной 99,73% можно утверждать, что диапазон значений рН для здорового человека составляет 6,8 – 8.