В теории ошибок величину

S = (38)

называют средней квадратичной ошибкой прямо измеряемой величины х, величину х (см. (36)) – её абсолютной ошибкой, а величину  =  100 % – относительной ошибкой, оценивающей точность измерений.

При косвенных измерениях искомую величину Z вычисляют по некоторой формуле

Z = f(x, y),

где x и y – прямо измеряемые величины.

Число значений x и y, полученных при измерении каждого из них, равно n:

x₁, х₂, х₃, …., х_n ;

у₁, у₂, у₃, … , у_n.

Теперь можно найти их средние арифметические значения:

=,=(39)

и средние квадратичные ошибки:

S_x = 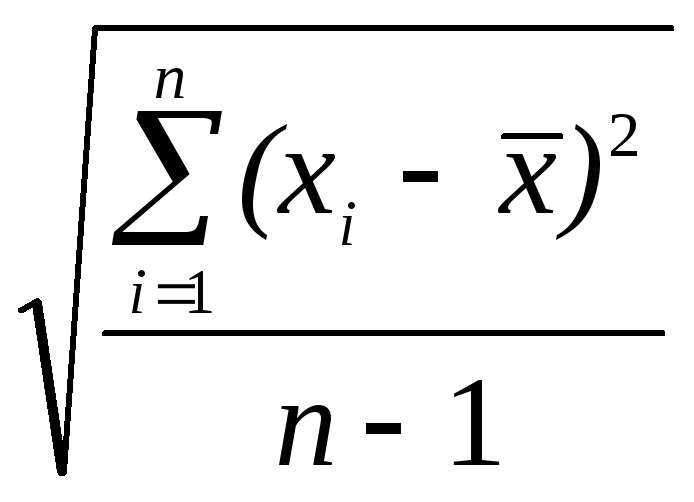; S_у = , (40)

Среднее арифметическое значение косвенно измеряемой величины вычисляют по формуле

= f(). (41)

Истинное значение Z – Z_ист. лежит в доверительном интервале:

– Z < Z_ист. < + Z или Z_ист.= ± Z. (3.7.5)

Полуширина данного интервала для нормально распределенной величины Z рассчитывается по формуле:

Z = t_{, n}. (43)

В (43) средняя квадратичная ошибка S_z косвенно измеряемой величины, равна:

= , (44)

где =Z_x´ и =Z_y´ – частные производные величины Z=f(x, y), соответственно, по x и по у, вычисляемые при их средних значениях, S_x и S_у – средние квадртичные ошибки величин х и у, значения которых получаются по формулам (40).

Окончательный результат обычно записывается в виде: Z_ист. =  Z, с указанием выбранного значения . Приводится так же относительная ошибка косвенно измеряемой величины:

 =  100 %.

Пример. Рассчитаем случайную ошибку при косвенном измерении вязкости жидкости:

 = ₀,

где , , t – вязкость, плотность и время истечения исследуемой жидкости из капилляра вискозиметра; ₀, ₀, t₀ – соответственно вязкость, плотность и время истечения эталонной жидкости (воды).

Величины ₀, ₀ и  считаем точно известными, t и t₀ измеряем секундомером, вязкость исследуемой жидкости – косвенно измеряемая величина.

1. Пять измерений времени истечения исследуемой жидкости и воды дали следующие результаты:

для исследуемой жидкости t= 79, 2с;80,4с;78,0с; 83,6с; 80,2 с;

для воды t₀ = 51,0с; 48,4с; 50,6с; 47,4с; 44,2с.

2. Найдем по (39) средние арифметические значения t и t₀:

= = 80,28 с,

= = 48,32 с.

Определим по (41) среднее арифметическое значение вязкости исследуемой жидкости при:  = 790 ,₀ = 998,2 ,₀ = 1,0  10^-3 Па  с:

= ₀;= 1,0 10^-3  = 1,31 10^-3 Па с = 1,31 мПа с.

3.Рассчитаем среднюю квадратичную ошибку вязкости по (44):

S_ = .

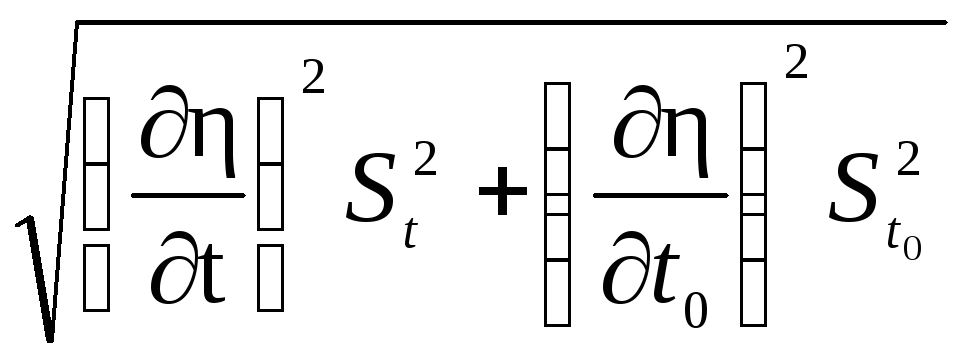Для этого по (40) определим средние квадратичные ошибки времени истечения исследуемой жидкости S_t и воды :

S_t = =2,09 с

= = 2,75 с.

Найдем частные производные приt = и t₀ = ₀:

= = = 16,38  10^-6 Па ,

= - = – = -27,21  10^-6 Па.

Тогда S_ = = 82,2  10^-6 Па  с.

4. Определим полуширину доверительного интервала или абсолютную ошибку вязкости  по (43). Для этого, приняв доверительную вероятность  = 0,95, и, зная число измерений непосредственно определяемых величин (n = 5), найдем коэффициент Стьюдента, [cм. табл., напр. в (4, 9)], t_{, n} = 2,78, тогда:

 = 2,78  = 0,1 10^-3 Па  с = 0,1 мПа  с.

Следовательно, с доверительной вероятностью  = 0,95 = 95% истинное значение вязкости исследуемой жидкости лежит в интервале

η =  = (1,31  0,1)  10^-3 Па  с = (1,31 0,1) мПа с.

Относительная ошибка равна

 =  100 % =  7,6 %